Bonjour,voici un exo que je traite:
1.jpg
2.png
3.png
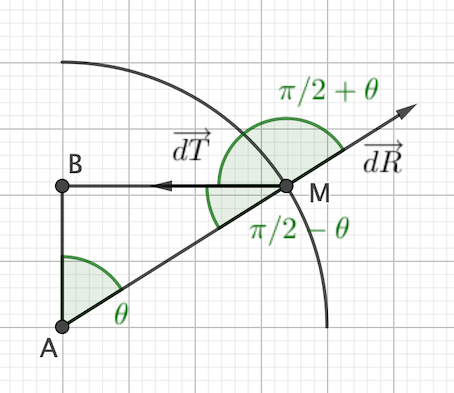
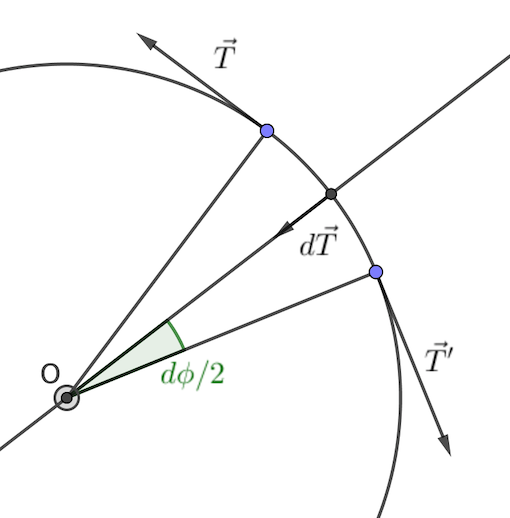
Lorsque je fais le bilan des forces appliquées sur l'élement élastique de longueur dl,je trouve qu'il est soumis à son poids,la réaction normale de la sphère (sans frottements),les forces appliquées par le reste de l'élastique sur cet élement là et les forces élastiques de chaque coté de l'élément élastique.Je ne comprend pas pq on a pas pris en compte ces forces là ??
Merci.
Quelle différence faites-vous entre "forces ... du reste de l'élastique" et "forces ... de chaque coté de l'élément"" ?Envoyé par itslunyitsluny
"aux tensions des parties gauche et droite de l’élastique sur le petit morceau" : elles sont bien prises en compte.
-Les "forces ... du reste de l'élastique" sont des forces appliquées par le reste de l'élastique sur l'élément qu'on étudie.
-Les "forces ... de chaque coté de l'élément" sont des forces qui viennent du caractère élastique.je crois qu on peut les ecrire de cette facon:
F(ϕ)=K(Rsin(θ)ϕ-l0)eϕ
F(ϕ+dϕ)=-K(Rsin(θ)(ϕ+dϕ)-l0)eϕ
K la raideur de l element de longueur Rsin(θ) dϕ, donc K=(k Rsin(θ)dϕ)/l0
Je ne sais si l'expression est correcte.En tout cas pour moi les deux forces :"forces ... du reste de l'élastique" et ""forces ... de chaque coté de l'élément" ne signifient pas la meme chose.Si ce n'est pas le cas,veuillez m'expliquer pourquoi.
Merci
Une force c'est l'action de qqch sur qqch
"forces ... du reste de l'élastique" sont des forces appliquées par le reste de l'élastique sur l'élément qu'on étudie. Cela répond donc à la définition.
Les "forces ... de chaque coté de l'élément" sont des forces qui viennent du caractère élastique, mais la force de quoi sur quoi ? si ce n'est pas du reste de l'élastique sur l'élément, elles viennent d'où ces forces ?
si on tire un ressort et on le laisse,il va faire des aller-retour grâce à la force de rappel.dans ce cas la force de rappel n'est pas appliquée par qqch sur le ressort,n'est ce pas?
Prenons l'exemple simple d'un ressort qu'on tire par les deux bouts puis qu'on lâche les deux bouts.
On va oublier le poids.
La résultante des forces est nulle (0 d'un côté, 0 de l'autre), G ne bouge pas.
Par contre, il se déforme et pour étudier la déformation, il faut faire un découpage comme votre élastique.
Et si on travaille dans le cas que vous proposez,on prend un découpage en x, x+dx.Normalement c'est comme si on obtient un petit ressort de longueur dx qui est tiré deux deux cotés par deux forces T(x+dx) et -T(x).Sa réponse pour retrouver sa taille normale est représentée par deux autres forces qui sont des forces de rappel,qu'on notera F(x+dx) et -F(x).Veuillez m'expliquer pourquoi vous considerez que F et T c'est la meme chose.
T est l'action du reste du ressort sur l'élément et F l'action de l'élément sur le reste du ressort et T=-F.
C'est la "même chose", sauf qu'on considère dans un cas l'action de A sur B et dans l'autre l'action de B sur A.
D'accord.
cette expression est elle correcte ?F(ϕ)=K(Rsin(θ)ϕ-l0)eϕ
F(ϕ+dϕ)=-K(Rsin(θ)(ϕ+dϕ)-l0)eϕ
De deux choses l'une :
- soit vous calculez du point de vue de l'élément : la longueur de l'élément estde laquelle vous retirez la proportion de l0 constituant la longueur à vide de l'élément
- soit vous calculez de l'extérieur et la longueur est
Quand on calcule un allongement l-l0, il faut bien sûr que l et l0 correspondent au même système.
Ah oui j'ai pas fait attention à l0.
F(ϕ)=K(Rsin(θ)-l0/2pi)dϕeϕ=-T(ϕ)
F(ϕ+dϕ)=-K(Rsin(θ)-l0/2pi) dϕeϕ =-T(ϕ+dϕ),est ce que k est independant de la taille de l'element (i.e on ne definit pas une raideur lineique)
donc l equation est: dm a = T(ϕ+dϕ)-T(ϕ)+P+R
k dépend en effet de la taille de l'élément, ici vous pouvez considérer que vos éléments sont en série et que la raideur totale est K, celle du ressort.
Mais la deuxième méthode évite ce calcul supplémentaire.
Remarque : en pas oublier que
donc si je note K la raideur totale du ressort de longueur à vide l0, alors la raideur de l'element étudié est k=K R sin(θ) dϕ/l0k dépend en effet de la taille de l'élément, ici vous pouvez considérer que vos éléments sont en série et que la raideur totale est K, celle du ressort.
Honnetement j'ai pas bien compris la 2eme methode.Est ce que vous donnez directement la force que subit tout l'elastique? si oui comment vous determinez le vecteur unitaire?Ca sera mieux peut etre d'écrire l'expression de la force et de l'expliquer.Mais la deuxième méthode évite ce calcul supplémentaire.
Merci.
Les éléments sont en série et, en série, c'est l'inverse des constantes qui s'ajoutent "donc" (avec "N" nombre de ressorts et des notations très abusives)
Pour éviter cela, on peut mettre en forme, mais le plus simple est de prendre le ressort en entier de longueur à vide l0, de longueur ..., d'allongement ..., donc de force=
Bonsoir,
dans cette image je ne comprend pas 2 choses:
-Pourquoi dT est perpendiculaire (comment on a pu trouver cette représentation?)
-Je ne vois pas comment réaliser le produit scalaire entre dT et la normale à dR.
Merci.
Pour l'angle, par ex.
On peut aussi tracer une verticale en M
Pour la direction de dT
T et T' sont parallèles au fil donc horizontaux dT=T+T' aussi
T et T' sont de même intensité dT=T+T' est sur la bissectrice.
Bonjour,j'ai pas bien compris.
Pour la direction:
dT=T(ϕ+dϕ) eϕ(ϕ+dϕ) -T(ϕ)eϕ(ϕ)
T(ϕ+dϕ)=T(ϕ) donc
comment vous deduisez la direction de cette expression?
Pour l'angle,j'ai compris mles angles que vous avez mis.
Mais,c'est quoi alors la projection de dT sur la normale à dR?
(d'ailleurs il n y a pas une seule normale)
J'ai plutôt tendance à faire cela géométriquement :
Sinon, vous devez reconnaitre qqch que vous avez vu en cinématique du point, la dérivée d'un vecteur unitaire
La "normale" est en effet le plan tangent à la boule. Mais la partie utile est l'intersection avec la plan (T,P), donc la tangente au cercle de la figure.
