Bonjours,
je souhaite comprendre d’où vient la formule de l'accélération dans le repère de frenet.
Pour rappelle c'est celle-ci:
a =
J'ai donc visionné cette vidéo: https://youtu.be/MFbWnT859aY?si=UiQzYxmgT2seL3HP
J'ai mis un commentaire pour expliquer mon problème (vous pourrez le lire, il y a les indicateurs temps de mes incompréhensions) mais étant donné que la chaine n'est plus actif je doute d'avoir une réponse.
Le problème est que dans la démonstration, il considère que la vitesse angulaire est une constante mais pas la norme de la vitesse. Or si la vitesse angulaire est une constante la norme de la vitesse devrait aussi l’être. Et si la norme de la vitesse est variable, la vitesse angulaire devrait aussi l’être.
J'ai donc l'impression que cette formule ne s'applique qu'à des mouvements dont la vitesse angulaire est constante et donc la norme de la vitesse aussi. En d'autres mots, qu'à des mouvements circulaires uniformes. Dans les autres cas, la formule ne serai pas appropriée.
Merci de m'éclairer.
-----



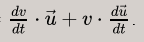

 . En revanche la démonstration peut se faire sans cette hypothèse. Dans la démonstration, on dérive la fonction
. En revanche la démonstration peut se faire sans cette hypothèse. Dans la démonstration, on dérive la fonction 