Transformée de Fourier

[corentinca]

Bonjour je souhaite réaliser la transformée de Fourier de ce signal :


Il s'agit d'un courant J induit par le mouvement des électrons libres dans un plasma. Mais ce n'est pas important pour comprendre la suite.

Voici mon code matlab :

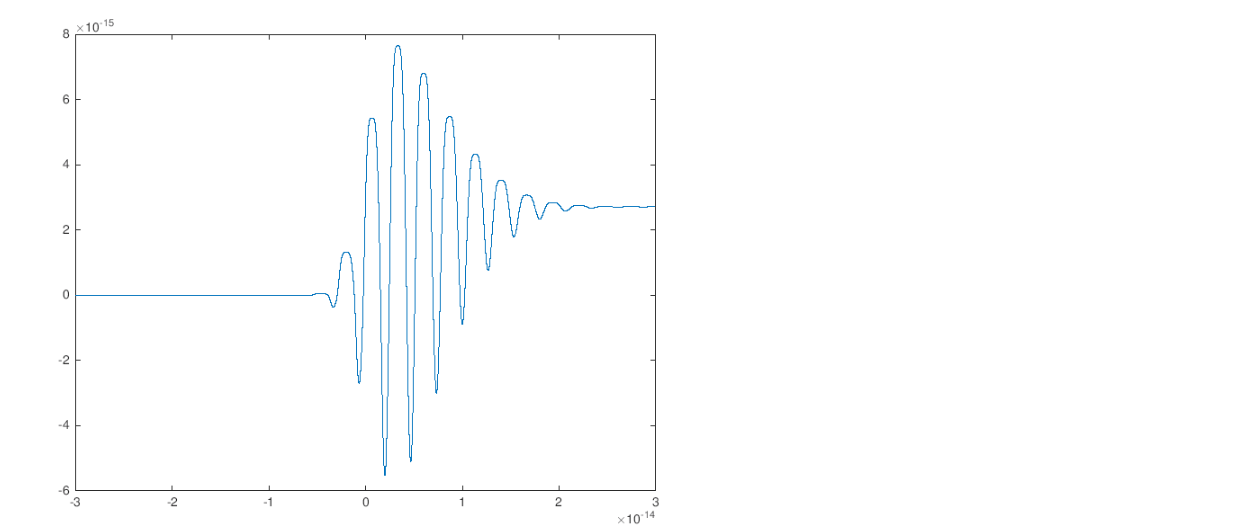
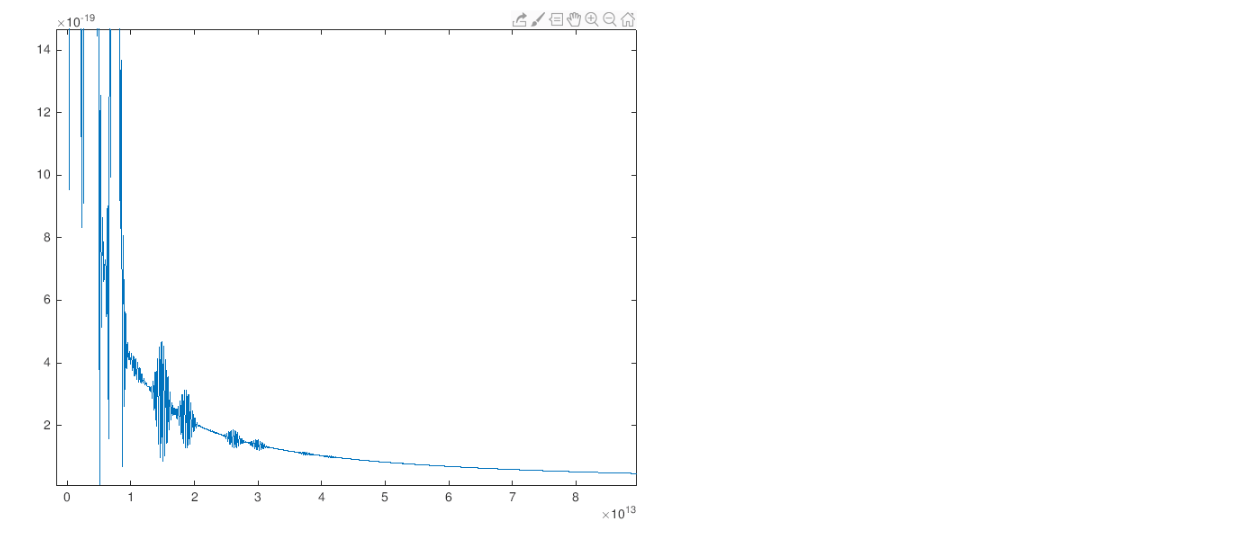
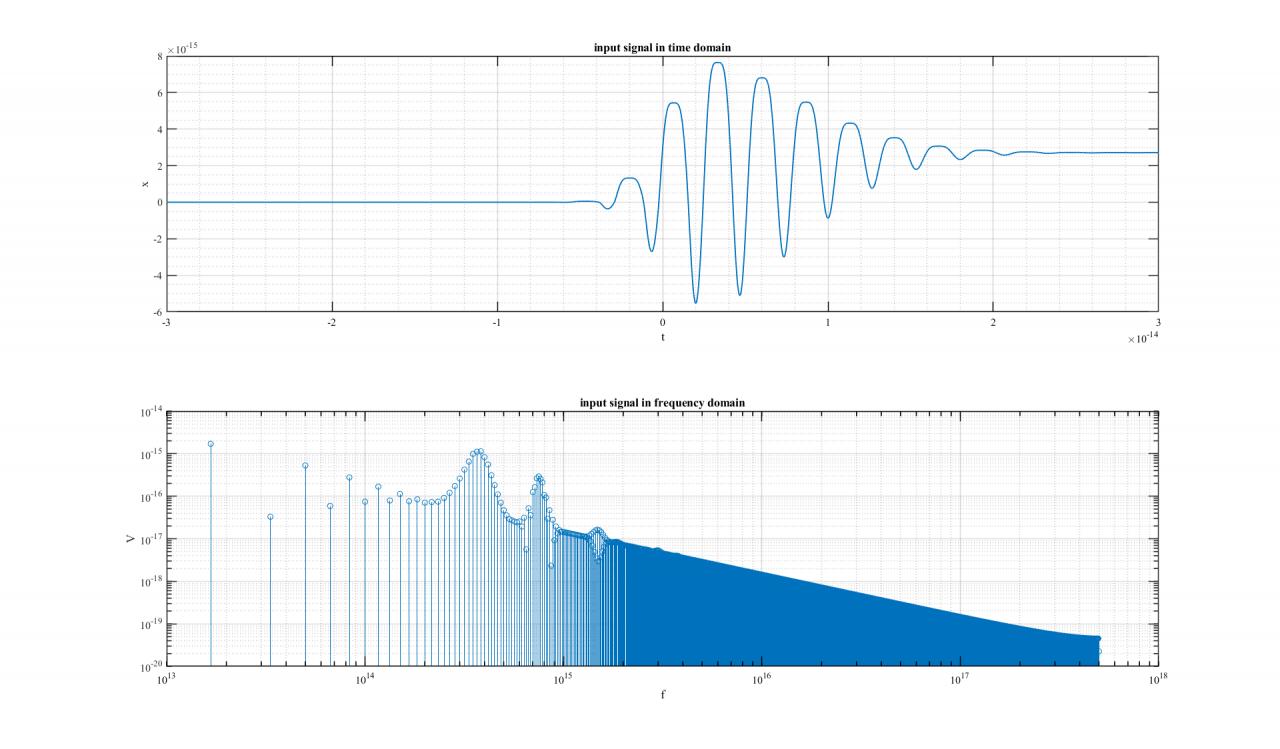
%Unité
eV = 1.6*10^(-19);%electronvolt
nm = 1.0*10^(-9);%nanometre
c = 3.0*10^(8);%vitesse de la lumiere
nu0 = 1.26*10^(-6);%constante 
Ui = 13.6*eV;%energie ionisation
me = 9.1*10^(-31);%masse électron
e= eV;
nuau = 4.13*10^16;%constante
Uau = 27.21*eV;%constante liéeau laser
Eau = 5.14*10^11;%constant liée au laser
%Parametre du laser
 
I=10^18;%intensité laser
lambda = 800*nm;%longueur d'onde
E0 = sqrt(2*nu0*c*I);%amplitude champ électrique
omega = 2*pi*c/lambda;%fréquence
phi = pi/2;%phase entre les deux couleurs du  laser
r = 0.2;%energie de la deuxième harmonique par rapport a la premier
tp1 = 10^(-14);%impulsion (temps) de la fondamentale
tp2 = 10^(-14);%impulsion(temps) de l'harmonique
nb_pts = 60000;%nb points
pas = 6*tp1/nb_pts;%%résolution
t = -3*tp1:pas:3*tp1;%vecteur temps
E= E0*( sqrt(1-r)*exp((-t.^2)/(tp1^2)).*cos(omega.*t)+sqrt(r)*exp((-t.^2)/(tp2^2)).*cos(2*omega.*t +phi));%champ
%calcul taux ionisation 
alpha = nuau*Eau*2*(2*Ui/Uau)^(5/2);%facteur ionisation
beta = (4/3)*(Ui/Uau)*sqrt(2*Ui/Uau)*Eau;%deuxième facteur ionisaation
W = zeros(1,nb_pts+1);
%densité electronique 
integ =zeros(1,nb_pts+1);
  for i =1:nb_pts+1
      if sqrt(E(i)^2)==0
        W(i)=0;
      else 
          W(i) = (alpha/sqrt(E(i)^2)).*exp(-beta/sqrt(E(i)^2));%calcul ionisation
      end 
      if i~=nb_pts+1
        integ(i+1)=integ(i)+W(i)*pas;
      end 
end 
Z  = 1.-exp(-integ);%calcul de la densité électronique induite
Z1 = Z/max(Z);
Na=10^13;%densité atomique initiale
E1=E./(2*max(E));
W1=W./(2*max(W));
J = zeros(1,nb_pts+1);%courant induit
for i = 1:nb_pts
    J(i+1) = J(i) + (e^2)/(me)*Z(i)*E(i)*pas;%calcul du courant induit
end 
%plot(t,J)
Fs = 10^16;           % Sampling frequency
t = -50*10^-14:1/Fs:50*10^-14;  % Time vector 
L = length(t);      % Signal length
n = 2^nextpow2(L);  
Y = fft(J,n);%trasnfoirmér de fourier
f = Fs*(0:(n/2))/n;
P = abs(Y/n);
 
plot(f,P(1:n/2+1))

Tout est détaillé avec les %. Et vous voyez qu'a la fin du code j'essaye de faire la transformée de Fourier de mon courant J induit qui est une impulsion de -1x10^-14 a plus de 3x10^-14 secondes. DU coup j'ai rentré un vecteur temps entre -50 a 50 x 10^-14. le probleme c'est que j'obtient rien sur mon spectre j'ai genre une ligne droite sur zéro...
Pouvez-vous m'aider?
-----

[corentinca]

Voici le spectre que j'obtiens :



Je trouve que le spectre est "bizarre"

[Antoane]

Bonjour,

Dans le code, le vecteur J a pour longueur 60001, avec ses 18228 premiers éléments qui sont nuls. Or, n vaut 16384 ce qui fait q'en faisant fft(J,n), tu réalises la FFT des 16384 premiers éléments de J seulement, c'est à dire du vecteur nul. Normal alors de trouver un spectre nul.

La fft réalise une périodisation du signal, ce qui fait que tu ne réalises la fft de :

qui présente des discontinuités.

[Antoane]

En prenant l'intégralité du signal, je trouve la fft (désolé, j'ai l'habitude du log-log pour les spectres) :


On observe :
- la raie correspondant aux oscillations à 4e14 Hz et quelques harmoniques
- la décroissance en 1/f due au fondamental carré causé par la périodisation de la FFT.
Le résultat me parait donc assez cohérent.

[A voir en vidéo sur Futura]