Transformée de Fourier d'une liste

[Youyoube]

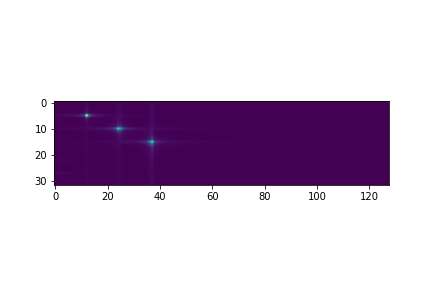
Bonjour je viens vers vous car je suis bloqué sur un travail. Mon objectif est de créer un modèle d'une source émettant un signal que j'ai programmé, ainsi que de 30 récepteurs qui interceptent ce signal. En conséquence, j'obtiens une liste des signaux captés par chacun des récepteurs. Ensuite, je veux faire la transformée de Fourier de ces signaux dans le temps et l'espace pour finalement représenter en 2D la longueur d'onde en fonction de la fréquence. Les vecteurs de fréquence et de longueur d'onde auront une fréquence et une longueur d'échantillonnage respectives, désignées par fe et ke.
Merci d'avance pour votre aide

 

#definition de la fonction récepteurs 

def modeleSR(N,Dsr,D):
    recepteur=[]
    I=0
    i=0
    while i <= N-1:
        signal_recu=toneburst(t-((Dsr+I)/c),t0,T,fc)
        I=I+D
        i=i+1
        recepteur=recepteur+[signal_recu]
    return recepteur

recepteur=modeleSR(N,Dsr,D) #la matrice avec les signaux de l'ensemble des récepteurs

-----

[gts2]

Bonjour,

Vous voulez programmer une transformée de Fourier ou l'utiliser.

Si c'est pour utiliser dans numpy.fft il y a tout ce qu'il faut.
Vous tenez à une liste ? Parce qu'avec numpy, il est préférable d'utiliser des nparray.

[pm42]

En effet :

https://numpy.org/doc/stable/referen...ines.fft.html#

Cette question aurait peut-être plus sa place en programmation qu'en physique.

[Youyoube]

Bonsoir, je vous remercie pour votre réponse. En fait, je ne suis pas obligé d’utiliser une liste, je peux utiliser les np.array. En ce qui concerne la suite du code, j’ai essayé de faire une transformée de Fourier sur le temps et sur l’espace en utilisant la FFT sur toutes les lignes et colonnes de la matrice, mais je ne suis pas sûr que ma méthode soit correcte pour pouvoir tracer le graphe attendu. Voici la suite de mon code :

recepteur=np.array(recepteur)
#TF sur le temps 

recepteur=np.pad(recepteur,(20,20)) #zero pading

def recepteur_spectres_freq():
    liste=[]
    for i in recepteur:
        spectre=np.fft.fft(i)
        spectre=np.fft.fftshift(spectre)
        spectre=(spectre)
        liste.append(spectre)
    return np.array(liste)

#TF sur la postion en plus 

def recepteur_spectres_posi_freq():
    mat1=recepteur_spectres_freq()
    liste=[]
    for i in mat1.T:
        spectre=np.fft.ifft(i)
        spectre=np.fft.fftshift(spectre)
        spectre=(spectre)
        liste.append(spectre)
    return np.array(liste).T


f = np.fft.fftshift(np.fft.fftfreq(len(recepteur_spectres_posi_freq()[0]),1/fe)) #vecteur frequence

k = np.fft.fftshift(np.fft.fftfreq(len(recepteur_spectres_posi_freq()),1/D)) #vecteur longueur d'onde

[A voir en vidéo sur Futura]

[gts2]

Bonjour,

Pourquoi un pad symétrique ? longueur des données ?
Pourquoi un ifft dans la deuxième procédure ?

Pour f et k
f = np.fft.fftfreq(longueur du signal,1/fe)
k = np.fft.fftfreq(nombre de récepteur,1/D)) #vecteur longueur d'onde (nombre d'onde ?)
suffit, non ?

[albanxiii]

Cette question aurait peut-être plus sa place en programmation qu'en physique.

Effectivement, c'est transféré.

[gts2]

J'ai trouvé pour le ifft : c'est lié au moins de exp(j(w t - k x) ?

Et votre procédure marche (j'ai fait quelques modifs de détail) et en testant avec la somme de trois sin(k(t-x)), j'obtiens :