Bonjour,
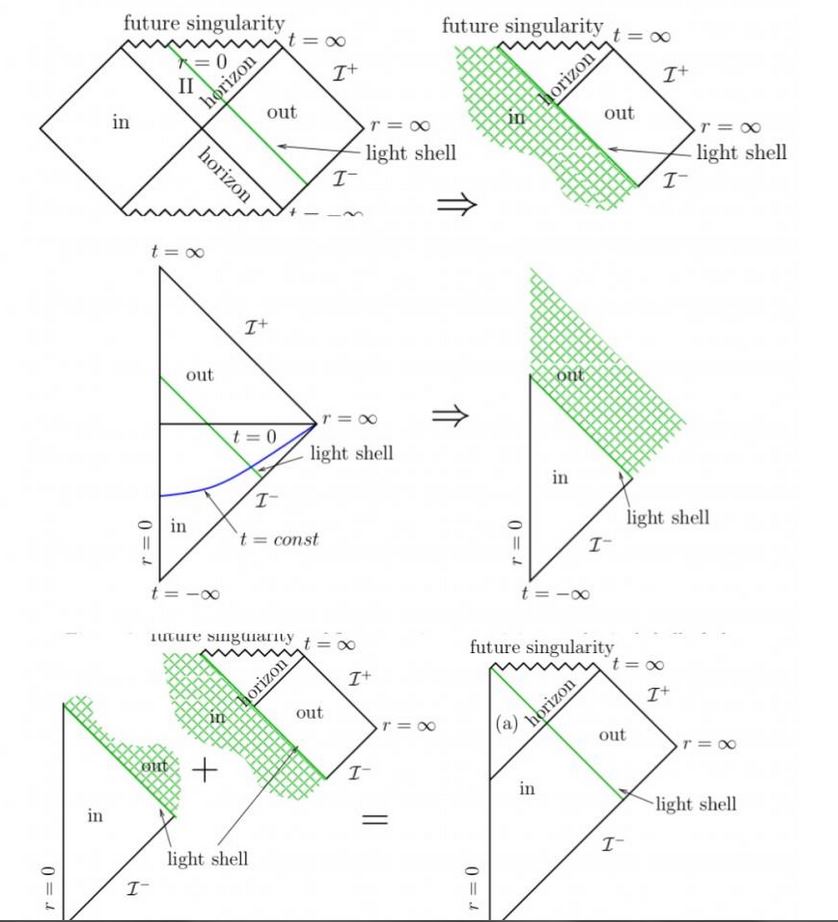
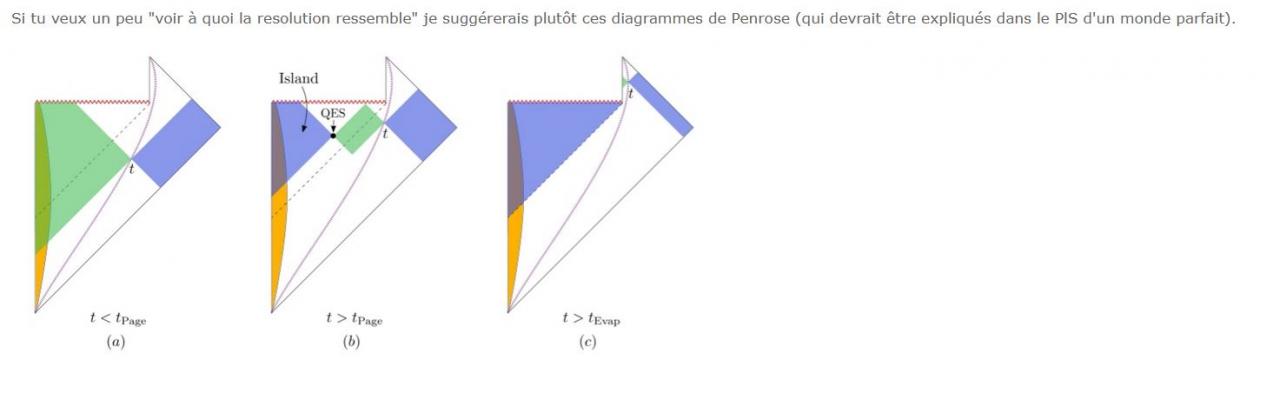
Pensez vous qu'il soit possible d'expliquer ou de "vulgariser "un peu les diagrammes de Penrose. Comment ils sont construits et à quoi ils servent ?
J'ai lu son livre les cycles du temps et la page wikipedia sur les diagrammes de Penrose, mais je n'ai rien compris à ceux ci ( sauf que ça à l'air d'être très compliqué )
Merci d'avance pour toute réponse
Salut,
j'ai une vidéo assez vulgarisée sur le sujet, mais je t'envoie ça par MP (pas d'auto-promotion). Et d'autres donneront peut-être des explications.
Compliqué, non sur le principe, oui techniquement (enfin, c'est pas la mer à boire, mais c'est quand même avec une transformation conforme et tout ça)
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
En plus du cours de DD, si l'anglais ne te rebute pas (sinon la traduction auto en français est dispo, et ce n'est pas de l'anglais compliqué), cette vidéo me semble pas mal.
Introduction to Penrose diagrams
Sinon ce cours en français m'a l'air pas mal du tout :
Schwarzschild et trous noirs
• Espace de Rindler
• Métrique de Schwarzschild
• Horizon du trou noir
• Derrière l’horizon
• Extension maximale
• Diagrammes de Penrose
• Formation d’un trou noir
• Zoologie
Dernière modification par Gilgamesh ; 04/10/2022 à 11h12.
Parcours Etranges
Merci pour vos réponse.
Je suis nouveau sur futura-sciences mais je trouve qu'au niveau de la réactivité et de l'interactivité c'est top. Si j'avais su je me serai inscrit avant
En terme de nombres de participants (y compris avec les qualifications appropries) et nombre de messages par jours, c'est le forum scientifique francophone le plus fréquenté. Donc forcément....Envoyé par pachacamac
Je suis nouveau sur futura-sciences mais je trouve qu'au niveau de la réactivité et de l'interactivité c'est top. Si j'avais su je me serai inscrit avant
Ceci dit il arrive qu'il y ait des messages sans réponses (souvent sur des sujets trop spécialisés).
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
Bonjour,
Ayant regardé un certain nombre de diagrammes de Penrose dans les derniers posts et ayant progressé sur les différentes métriques en particulier celle de Schwarzschild, j'ai maintenant plus de billes pour mieux les comprendre.
Donc je post ici, six de ces diagrammes en les numérotant comme une matrice : première ligne de gauche à droite diagrammes 1 et 2 deuxieme ligne diagrammes 3 et 4 , 3 ième ligne diagrammes 5 et 6 agrémenter de trois petites questions.
questions :
1 : Que ce passe t'il entre 1 et 2 ?
2 : dans le schéma 3 la ligne bleues représente une geodésique à t contant?
3: que représente le quadrillage vert dans 2 , 4 et 5 ?
MerciQuelques explications de mmanu_F accompagnant ces diagrammes : Plus précisément, si on considère un trou noir formé à partir d'une coquille de photons "en effondrement" (en vert sur la figure), on peut reconstruire le diagramme de Penrose en collant (au niveau de la coquille) la partie en haut à droite du trou noir éternel (1ère ligne) à la partie en bas à gauche du diagramme de Penrose d'un espace de Minkowski vide modulo la coquille (2ème ligne), l'intérieur de la coquille étant vide en conséquence du théorème de Birkhoff. Le diagramme de Penrose, Minkowski à l'intérieur, Schwarzschild à l'extérieur de la coquille, est représenté sur la 3ème ligne."
Dernière modification par pachacamac ; 14/12/2022 à 17h08. Motif: Correction balise
1) On découpe le diagramme 1 le long de la géodésique nulle verte (enfin, c'est en fait tout un cône sphérique de géodésiques nulles (chaque point du diagramme étant une sphère de rayon r), le diagramme 2 est le diagramme 1 duquel on a enlevé la partie inférieure (quadrillage vert)
2) la ligne bleue est une ligne à t constant (une tranche spatiale en fait), et comme il s'agit d'un espace-temps de Minkowski, c'est en plus une géodésique (une tranche spatiale qui contient des géodésiques de genre espace)
3) c'est ce que l'on a découpé et enlevé avant de recoller. On évide un cône de Schwarzschild, on taille Minkowski en pointe et on emboite les deux. Tout sous-entendu graveleux doit bien sûr être écarté
m@ch3
Never feed the troll after midnight!
Merci. J'ai bien compris. En fait les trois lignes des diagrammes nous précise comment découper et recoller.
Oui, mais au final ça donne quoi ce redécoupage ?
J'annule la question dont la réponse est : Le diagramme de Penrose, Minkowski à l'intérieur, Schwarzschild à l'extérieur de la coquille, est représenté sur la 3ème ligne.
Le diagramme final est le cas le plus simple (mais aussi le plus irréaliste!) d'effondrement donnant naissance à un trou noir.
Initialement, on a des particules de masse nulle qui convergent toutes vers le même point qu'elles atteindront toutes en même temps. Ces particules forment une coquille sphérique et c'est cette coquille qui s'effondre (à la vitesse de la lumière). La symétrie est sphérique.
En vertu du théorème de Gauss, la géométrie à l'intérieur de la coquille est celle de Minkowski.
En vertu du théorème de Birkhoff, la géométrie à l'extérieur est celle de Schwarzschild. En effet, cette coquille faite de particules de masse nulle est de masse non nulle ! Sa masse est la norme de la somme des 4-impulsion des particules de la coquille : les composantes temporelles (énergie) s'additionnent mais les composantes spatiales (impulsion) s'annulent toutes deux à deux.
Quand la coquille devient plus petite que son rayon de Schwarzschild, elle croise un horizon ("né" quelque temps plus tôt) qui délimite la région dont toutes les lignes d'univers aboutissent à la singularité. On a formation d'un trou noir.
Un point de détail, un observateur qui se trouverait sous le rayon de Schwarzschild ne remarquera absolument rien (pas de pesanteur, de force de marée, spaghettification etc) tant que la coquille ne l'aura pas atteint. Il ne sait même pas quand il passe l'horizon.
m@ch3
Never feed the troll after midnight!
Merci!
Aussi il semblerait d'après ce que j'ai cru comprendre des explications de mmanu_F dans ce post que même les derniers progrès théoriques au niveau du paradoxe de l'information pouvaient se traduire sous forme de diagrammes de Penrose.
Si quelqu'un y comprend quelque chose...
Toute lumière bienvenue.
Merci
Dernière modification par pachacamac ; 15/12/2022 à 15h25.
Là par contre, je passe mon tour. On atteint mes limites.
m@ch3
Never feed the troll after midnight!
Okay.
Je suis pas sur de savoir ce qu'est un "cône sphérique" , je connais cône et sphère mais j'arrive pas à me représenter un cône sphérique...
C'est comme le cylindre sphérique, mais en cône.
Plus sérieusement, le cône comme le cylindre sont des surfaces réglées. Il y a une génératrice, qui est un cercle (souvent on appelle cela la base) et des directrices qui sont des droites intersectant la génératrice dont on demande qu'elle soient parallèles pour le cylindre où qu'elles se croisent en un point pour le cône (le cylindre n'est en fait qu'un cône particulier, pour lequel le point de croisement des directrices est à l'infini). Si on ajoute une dimension, on peut considérer une sphère comme génératrice plutôt qu'un cercle, ce qui donne les cylindres sphériques et les cônes sphériques.
Point intéressant en passant, tout comme le plan euclidien est un cône particulier (celui où les directrices se croisent dans le plan contenant la génératrice), l'espace euclidien est un cône sphérique particulier (celui où les directrices se croisent dans l'hyperplan contenant la génératrice).
m@ch3
Never feed the troll after midnight!
Bonjour,
Peut-être trouverez-vous quelques informations intéressantes dans ces deux posts sur quanta magazine au sujet de cette approche au paradoxe de l'information:
https://www.quantamagazine.org/the-m...-end-20201029/
https://www.quantamagazine.org/netta...adox-20210823/
Les diagrames de Penrose ne sont rien qu'une façon de façon de dessiner ce qu'il se passe. Ils ne sont en aucun cas nécessaires à la vulgarisation de cette solution, ni du paradoxe lui-même, donc si vous voulez juste en comprendre un peu plus sur ces histoires de courbe de Page, il ne me paraît pas indispensable que vous compreniez les maths des diagrammes de Penrose en détail pour ce point précis.
Je n'ai pas le temps d'écrire une réponse détaillée mais les notions cruciales dans cette histoires sont celles d'entropie d'intrication, de "extremal surface" et "quantum extremal surface" dont la mesure de l'aire reproduit l'entropie d'intrication entre deux systèmes en théorie quantique des champs, de la même manière que l'aire d'un trou noir correspond à son entropie. Ces notions sont discutées dans les deux articles au-dessus.
Merci beaucoup.
Je vais lire très attentivement ces deux articles ( que je viens de survoler ) qui non seulement m'apporteront quelques informations intéressantes mais qui risque si j 'arrive à comprendre l'entropie d'intrication de me propulser à la pointe des connaissances dans ce domaine
En bonus quantamagazine offre une mine d'articles super intéressants.
