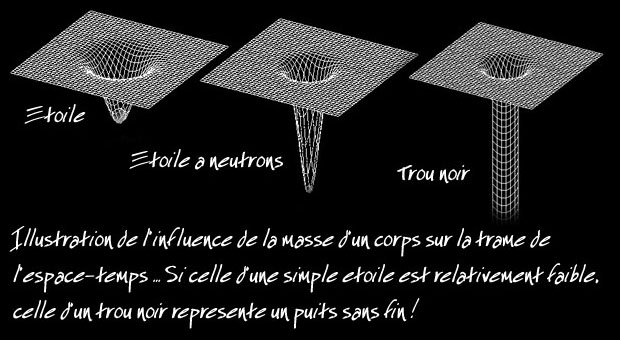
Bonjour à tous,
Déjà, pour voir si j’ai bien compris :
La singularité est par définition, quelque chose dont on a aucune idée, ce n’est donc pas un tout petit bidule avec des infinis partout.
Si la RG n’est pas valide pour décrire une singularité, alors pourquoi la serait-elle pour décrire l’intérieur d’un TN, à partir de juste derrière l’horizon ? si les courbes de la RG sont fausses à la fin (singularités), elles le sont dès le début, le début étant de juste derrière l’horizon.
Ma question est :
Suis-je dans l’erreur si je dis, qu’une fois passé l’horizon, on ne sait ABSOLUMENT RIEN ?
Et que ce puits gravitationnel infini, ne repose sur rien, à part une extrapolation de ce que l’on constate à l’extérieur, vers quelque chose dont on ne sait rien. Qu'est-ce qui m’empêche de dire, que passé l’horizon, je ne serais pas aspiré vers un centre qui n’existe pas, encore faut-il définir « exister » à l’intérieur.
Alors oui ! les TN engendrent une énorme gravitation, mais ce n’est pas une raison (c’est pourtant tentant) pour extrapoler notre connu vers un « endroit » ou toute notre physique est sans doute différente.
Mais si l’on croit, qu’une future théorie appelée « gravitation quantique » pourra expliquer comment des milliards de masses solaires peuvent exister dans un point, du haut de ma méconnaissance, je m’insurge.
Merci,
Vous pouvez taper maintenant !
-----





 En effet, pour la même raison pour laquelle on ne sait pas aller voir ce qui se passe sous l'horizon, ce qui se passe sous l'horizon n'a absolument aucun impact sur l'extérieur. Donc, ma fois, si on se trompe, ça ne changera rien !!!!
En effet, pour la même raison pour laquelle on ne sait pas aller voir ce qui se passe sous l'horizon, ce qui se passe sous l'horizon n'a absolument aucun impact sur l'extérieur. Donc, ma fois, si on se trompe, ça ne changera rien !!!!


 tu pourrais développer stp ?
tu pourrais développer stp ?