Démonstration dilatation du temps

[fabio123]

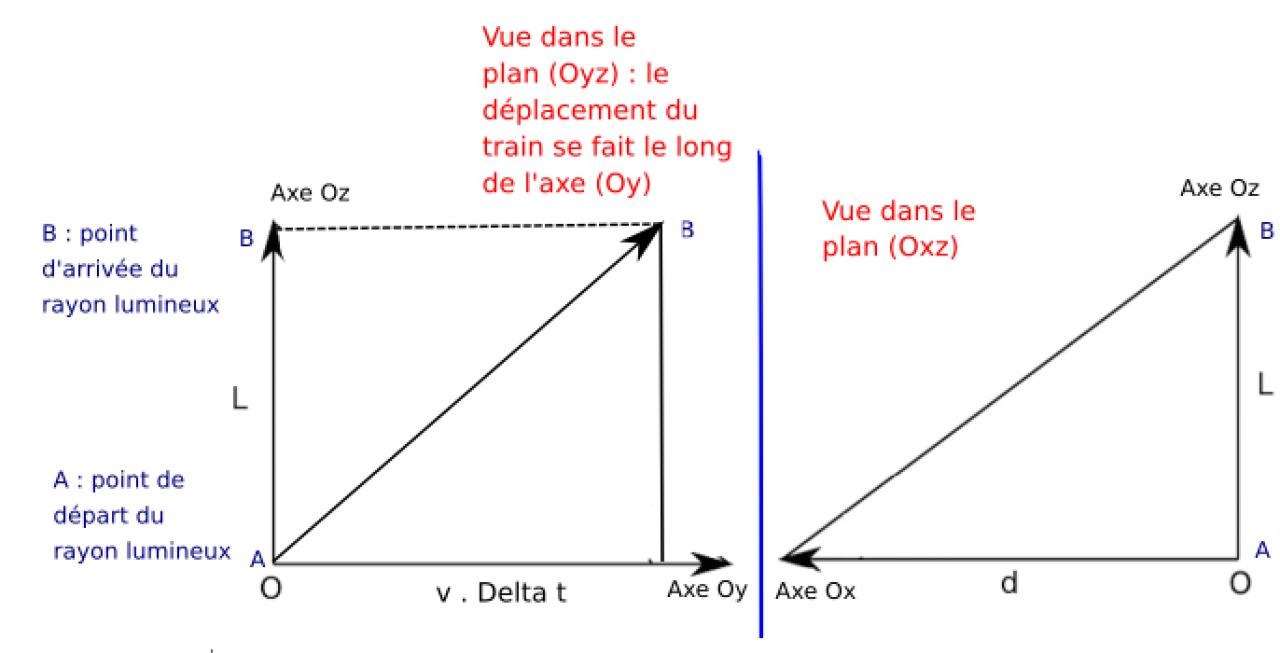
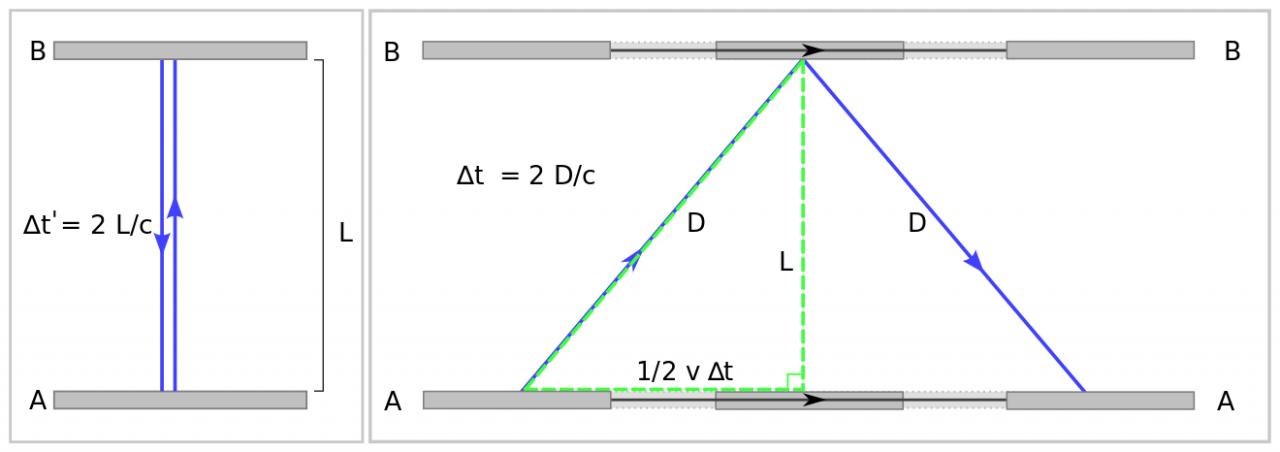
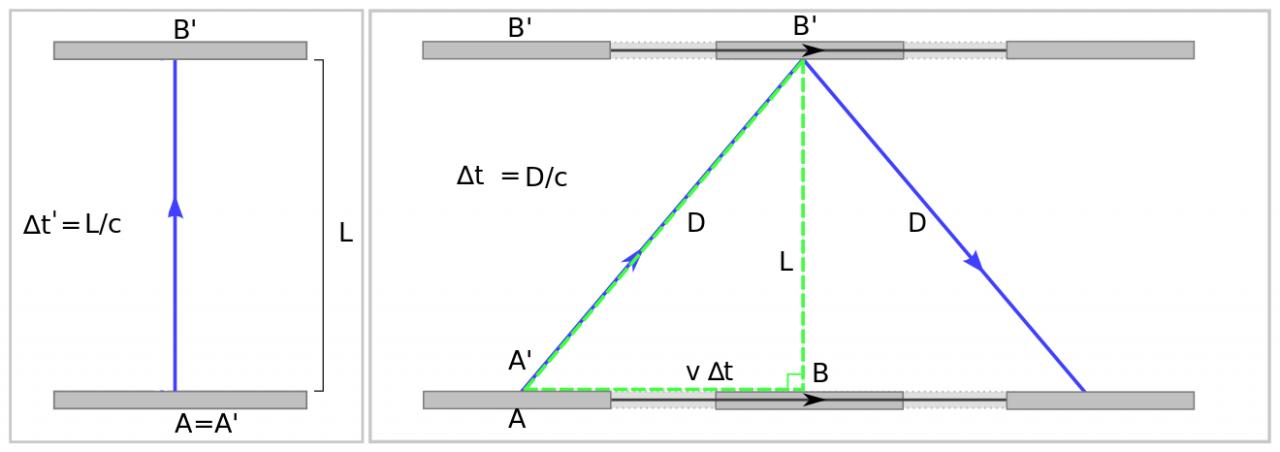
J'essaie de retrouver la formule de dilatation du temps entre un référentiel (R') se déplaçant à une vitesse v et un observateur fixe dans (R). Pour cela, je prends l'exemple que l'on retrouve souvent comme démo qui est celui d'un train dans lequel un rayon lumineux est émis verticalement (dans le train) : cette trajectoire verticale dans le train forme, avec le segment v*dt et la longueur verticale L que parcourt la lumière dans le train, à un triangle rectangle. Ceci est illustré sur le schéma de gauche de la figure en pièce jointe. Cela donne immédiatement avec Pythagore la relation:

ce qui donne :

et

Maintenant, j'aimerais retrouver la même formule mais en plaçant l'observateur de (R) à une distance "d" du plan (Oyz) (et avec z =0) et placé selon l'axe (0y) à l'endroit pile où la lumière atteint le bas du train (voir le schéma de droite sur la figure en pièce jointe). Si je prends les évènements (dans R) et , je trouve que pour l'observateur, l'intervalle de temps entre ces 2 évènements, en prenant :

une synchronisation commune pour (R) et (R'), c'est-à-dire à l'émission du photon du haut,



et





En prenant , je n'arrive pas à retrouver le facteur entre les 2 Delta.

Si je prends d=0 (l'observateur est considéré être dans le plan (Oyz) dans l'expression de ci-dessus, je trouve , ce qui est normal car l'observateur reçoit le photon du haut en même temps que le photon du bas est émis et qu'il reçoit donc instantanément ce dernier.

Dans la démonstration classique avec le triangle rectangle, comment peut-on considérer que l'observateur voit instantanément un triangle rectangle ? , c'est-à-dire que l'on ne prend pas en compte la distance entre ce triangle dans le plan(0yz) et l'observateur (qui est à une certaine distance sur l'axe (Ox) de mon schéma : dans mon exemple, je prends cette distance égale à "d").

toute aide est la bienvenue
-----

[fabio123]

Petite correction :

Si je prends d=0 (l'observateur est considéré être dans le plan (Oyz)) dans l'expression de ci-dessus, je trouve , ce qui est normal car l'observateur reçoit le photon du haut en même temps que le photon du bas est émis et l'observateur reçoit donc instantanément ce dernier.

[mach3]

Dans la démonstration classique avec le triangle rectangle, comment peut-on considérer que l'observateur voit instantanément un triangle rectangle ? , c'est-à-dire que l'on ne prend pas en compte la distance entre ce triangle dans le plan(0yz) et l'observateur (qui est à une certaine distance sur l'axe (Ox) de mon schéma : dans mon exemple, je prends cette distance égale à "d").

Je me trompe peut-être (pas tout à fait évident pour moi de bien comprendre ce qui est présenté), mais il me semble que c'est parce que l'on travaille dans une reconstruction de la réalité, et pas sur les perceptions directes que l'on en a. Personne ne voit instantanément ce triangle rectangle, il n'est visible que dans un schéma reconstruisant la situation.

Exemple le plus simple de ce que je dis :

Dans une reconstruction de la réalité, le temps propre d'un objet qui se déplace par rapport à moi est plus lent que mon temps propre, et cela quelque soit la direction de sa vitesse ou sa position. Dans les perceptions directes, je verrais (dans le sens avec mes yeux, en brut) le temps de l'objet ralenti quand il s'éloigne de moi et accéléré quand il s'approche de moi (et ralenti exactement du facteur de Lorentz si son mouvement est orthogonal à ma ligne de visée), c'est ce qu'on appelle l'effet Doppler. Pour passer des perceptions à la reconstruction, on prend simplement en compte le temps de parcours des signaux. Si à t=t0 je vois un évènement à d=d0 de moi, je vais reconstruire les choses en plaçant l'évènement en t=t0-d0/c.

m@ch3

[inviteec451e62]

La dilatation de temps répond à des lois de la relativité restreinte, si vous voulez trouver cette relation il faut aller à des articles de Einstein.

[A voir en vidéo sur Futura]

[invite49966480]

bonjour

est ce je peux poser une question

[inviteec451e62]

biensur c'est un forum ouvert

[Gilgamesh]

bonjour

est ce je peux poser une question

Uniquement si c'est en rapport avec le thème du fil (effet temporel relativiste).

[stefjm]

La dilatation de temps répond à des lois de la relativité restreinte, si vous voulez trouver cette relation il faut aller à des articles de Einstein.

Plutôt un bon cours d'aujourd'hui de relativité...

[fabio123]

Merci mach3 pour ton explication. j'ai mis en pièce jointe un schéma un peu plus précis illustrant ma première question :



Le train se déplace le long de l'axe (Oy) et la lumière va du point A vers le point B. (R) est le référentiel au repos et (R') celui du train en mouvement.

Je ne sais pas dans quel ordre procéder pour pouvoir reconstruire comme tu dis la réalité et obtenir ce triangle rectangle. Tout d'abord, est-ce que je peux considérer seulement 2 observateurs dans le référentiel au repos (R) ? Il me semble que leur position importe peu pourvu que l'on connaisse leur distance mutuelle avant l'expérience pour pouvoir les synchroniser, est-ce que c'est correct ? Il faut aussi connaître la distance entre la parallèle joignant les 2 observateurs et la droite parallèle du mouvement du train, c'est-à-dire l'axe (Oy).

J'essaie de faire les choses dans l'ordre, vos remarques sont les bienvenues s'il y a des erreurs.

1) Tout d'abord, les 2 observateurs synchronisent leur horloge car ils connaissant la distance qui les sépare.

2) Je poursuis, l'observateur "à gauche" reçoit dans (R) le photon issu de l'émission au point (A) dans (R').

Il note l'angle sous lequel il reçoit ce photon et connaissant la distance perpendiculaire au mouvement du train, il en déduit la distance à laquelle a eu lieu l'émission et donc cette émission s'est produite à .

3) l'observateur "à droite" dans (R) reçoit le photon issu de la réception au point (B) dans (R'). Idem, il en déduit la distance à laquelle a eu l'émission au point (B) et le décalage temporel par rapport à lui, c'est-à-dire

4) Les 2 observateurs "reconstruisent" ce qu'il s'est passé en comparant leurs résultats afin de les mettre en relations.

On peut donc écrire :

Pour l'instant, je prends (ça sera intéressant de prendre le cas où

Cela donne :



avec

J'obtiens alors :

avec qui est la distance réelle parcourue par le train durant l'intervalle .

Finalement, j'obtiens :



A partir de cette equation eq(1), je n'arrive pas à retrouver la relation classique de la dilatation du temps, à savoir :

A cause du triangle rectangle qui est une reconstruction de ce qui se passe vraiment, je pense qu'il faut assimiler dans eq(1) à dans la relation classique. Cette relation classique s'obtient en appliquant le théorème de Pythagore sur ce fameux triangle rectangle :

avec

Si quelqu'un pouvait voir ce qui cloche pour retrouver cette formule classique à partir de eq(1) ... Merci

[fabio123]

Cela donne :



avec

ici, je prends

[Mailou75]

Salut fabio,

Peut etre que ce dessin pourra t'aider : http://forums.futura-sciences.com/as...ml#post5034251
C'est a peu pres la meme histoire que la tienne : Un gardien de phare tire un laser sur le mousse d'un bateau.

Dans le dessin de gauche, la pointe tout en haut represente le moment où le gardien et le vigie (en haut du mat de meme hauteur que le phare) sont au meme point. Le gardien tire alors. Le mousse voit son assassin au moment où il recoit le rayon. Le gardien et le vigie verront le cadavre du mousse en meme temps.

Cette figure est un Minkowski 2D+t, attention le temps va vers le bas. Elle synthetise les trajets dans l'espace temps et les decalages temporels (symbolisés par les points qui sont le temps propre regulier de chacun).

La figure de droite decrit exactement la meme chose dans le repere du bateau. On voit que la lumiere y voyage verticalement, comme la lumiere dans ton train...

Bon courage

[Mailou75]

Le gardien et le vigie verront le cadavre du mousse en meme temps.

Ambigu... Le gardien sera plus vieux a la reception et le "vigie voyant le mousse mort" est un evenement qui est synchronisé au temps du gardien dans son espace (ce qui n'est pas vrai pour le vigie)

[Zefram Cochrane]

Salut,
Pour la lanterne du mât du bâteau:
Soit le Vigie (Orange), le Gardien du phare (Rouge) , le Mousse au pied du mât (Vert) et le Naufragé sur une île (Bleu)
si c'est le Mousse qui est visé alors, Orange devra tirer verticalement le long de l'axe du mât et Rouge devra anticiper la position de Vert.
Si c'est le Naufragé qui est visé, alors Rouge devra tirer en oblique et Orange devra tirer verticalement le long de l'axe du mât pour anticiper la position de Bleu.

Lorsque le Mousse où le Naufragé sera atteint par les tirs,
le Mousse verra le Vigie et le Gardien du phare à sa verticale et le Naufragé les verra en oblique (ainsi que le mât).


Ce schéma présente les deux perspectives: celle de Bleu en permier plan et celle de Vert en arrière plan (ie avec un effet de transparence)

[Mailou75]

Pour V=0,6c je suis d'accord avec la courbe du phare vue par le mousse

[invite6c093f92]

@Mailou et ZF...Heu vous avez déjà pourri le thread de Disciplusimplex...vous voulez pas au moins attendre une réponse de Fabio123 histoire de voir si ça l'aide vos histoires pour éventuellement continuer??? Par politesse...

Je dis ça, parce que vs avez par l'air de vous rendre compte que quand vous arrivez sur un fil de Relat, tout le monde (et surtout le questionneur) se barre...cela devrait vous interpeller je pense

[Deedee81]

Bonjour,

Mailou, ZF, c'est un peu HS donc au minimum, peut-être ouvrir un fil pour discuter de certains points particuliers

[Zefram Cochrane]

Bonjour Didier, bonjour Deedee.
C'est toujours le même problème avec la dilatation du temps et la contraction des longueurs

on en arrive à cette conception qui est fausse.
en l'occurence Fabio essaye visiblement d'en sortir d'où ses calculs.

On retrouve toujours la même erreur.
Si Vert (le Mousse) passe le travers de la base du phare à T=T'=0s en MRU à V=0.6c, il atteint Bleu (le Naufragé)distant de X=36s.l en une durée coordonnée T=60s soit une durée propre de T°'=48s d'où un coefficient de dilatation temporel de T/T°' =1.25
Fabio essaye de trouver une méthode géométrique pour trouver la relation inverse et ses calculs on tendance à lui raconter que pour une durée porpre de T°=60s dans le système de coordonnée de Bleu, il s'écoule une durée coordonnée de T'=T°*1.25=75s; ce qui est juste du fait de la relativité de la simultanéité mais ne correspond pas au résultat attendu qui est T°'=48s.

C'est normal le terme de dilatation du temps est trompeur (amusez vous à calculer la durée coordonnée écoulée à bord d'une fusée accélérant et passant le travers d'une bouée stationnaire pour chaque seconde de durée propre écoulée pour la bouée et vous allez rigoler).

Mailou a raison de rappeler l'analogie avec l'expérience de la lanterne du mât du bâteau, et mon schéma à le mérite de montrer que pour Bleu, le Vigie Orange et le Gardien du Phare Rouge sont à 60s.l de distance en oblique et que pour Vert, Rouge et Orange se trouvent à sa verticale à 48s.l de distance.

Pour moi on est clairement pas HS sur ce fil.
Cordialement,

P.S est ce que mon schéma existe dans d'autres ouvrages ou sur le Net?

[Lansberg]

Bonjour,

A partir de cette equation eq(1), je n'arrive pas à retrouver la relation classique de la dilatation du temps, à savoir :

c'est peut-être normal, vu qu'en RR le temps de propagation entre les référentiels n'est pas pris en compte !
Il faut peut être s'intéresser aux illusions relativistes dans lesquelles, justement, le temps de propagation intervient (voir chap 3) :

https://books.google.fr/books?id=7e8...reinte&f=false

[Deedee81]

en l'occurence Fabio essaye visiblement d'en sortir d'où ses calculs.

Il n'empêche que tu es HS (et donc tu pourris le fil d'un autre). Fabio demande comment conduire un jet-ski, tu lui donnes le manuel pour conduire le Grand Princess.

[Mailou75]

Bonjour,

Pardon si ça pollue, à la base je pensais aider (car c'est le même problème donc pas HS) mais je suis d'accord pour attendre un retour de Fabio avant de tartiner de la formule et de l'application numérique. L'idée était de lui faire comprendre la logique générale, voyons sa réaction...

A+
(Mode pause)

[Zefram Cochrane]

Bon. Je vais faire l'effort de me plonger dans les calculs de Fabio (un regard objectif cela va de soi) :

Pièce jointe 353130

Le train se déplace le long de l'axe (Oy) et la lumière va du point A vers le point B. (R) est le référentiel au repos et (R') celui du train en mouvement.

1) Tout d'abord, les 2 observateurs synchronisent leur horloge car ils connaissant la distance qui les sépare.

Je n'arrive pas à situer les deux observateurs au premier coup d'oeil sur le schéma.
D'après les positions de A et de B j'en déduit que A et B apprtiennent à R' (il aurait mieux valu les noter A' et B')

2) Je poursuis, l'observateur "à gauche" reçoit dans (R) le photon issu de l'émission au point (A) dans (R').

cet observateur doit être situé au point B dans R (coincidant avec B' dans R'), mais ignorant la position du second observateur, j'ignore à quoi correspond la distance qui les sépare.

Il note l'angle sous lequel il reçoit ce photon et connaissant la distance perpendiculaire au mouvement du train, il en déduit la distance à laquelle a eu lieu l'émission et donc cette émission s'est produite à .

Donc da correspond à priori à la distance entre A et B dans R

3) l'observateur "à droite" dans (R) reçoit le photon issu de la réception au point (B) dans (R'). Idem, il en déduit la distance à laquelle a eu l'émission au point (B) et le décalage temporel par rapport à lui, c'est-à-dire

Ici il y a un problème car soit les deux observateurs sont dans R et sont en B à la réception cela donne que la distance qui les sépare est nulle. Mais, vu les schéma.
J'en déduis que l'observateur de gauche O' se trouve en B' à T'=T=0s et distant de A' d'une distance . et que à T=0s, l'observateur de droite O se trouve en B à une distance :
de A (coïncidant avec A' à T=T'=0s)

4) Les 2 observateurs "reconstruisent" ce qu'il s'est passé en comparant leurs résultats afin de les mettre en relations.

On peut donc écrire :

Je ne vais pas plus loins parce que je manque de temps, mais il me semble plus judicieux pour comparer les résultats de pendre

P.S je n'ai clairement pas suivi la même méthode pour établir mon schéma...

[fabio123]

Merci pour votre aide. J'essaie de faire la similitude entre mon expérience du train et celle du gardien de phare qui tire sur le mousse.

Dans mon cas, si je prend les 2 observateurs dans le même plan que celui du train (c'est-à-dire avec une distance perpendiculaire au mouvement du train qui est nulle pour les 2 observateurs), je pense qu'il y a équivalence entre les 2 expériences.

Ce qui me chiffonne, c'est que je peux uniquement avoir la relation :

avec et l'intervalle de temps écoulé dans le référentiel en mouvement R' (le train).

et non :

où est la différence entre le temps mesuré par les 2 observateurs (temps quand l'observateur (situé sur la gauche) reçoit le photon issu de l'évènement A et le temps de l'observateur (situé sur la droite) qui reçoit le photon issu de l'évènement B) une fois l'expérience terminé et qu'ils comparent leur résultat : on peut écrire que

ça détruit un peu mon mythe de croire qu'en prenant un référentiel (R') animé d'une vitesse v, un observateur dans un référentiel fixe (R) a un temps qui s'écoule selon , raison pour laquelle ça me chiffonne. D'après ce que je comprends, le dans cette équation précédente correspond à et non l'intervalle "classique" égal à la différence de 2 temps mesurés par 2 observateurs différents mais synchronisés.

Peut-être est-ce du au fait qu'il y ait, dans mon expérience , 2 observateurs dans le réferentiel fixe (R) et non 1 seul comme dans le référentiel (R') du train ...

Si vous pouviez voir où est la coquille ...

[fabio123]

voici un schéma qui résume l'expérience, ressemblant à celui du gardien et du mousse, mais en ne considérant qu'un aller de A vers B (on enleve le facteur 2 et 1/2)



le correspond à mon

[fabio123]

c'est peut-être normal, vu qu'en RR le temps de propagation entre les référentiels n'est pas pris en compte !

Ah dans ce cas-là, il n'y a plus de problème, je pensais qu'il fallait en tenir compte. Du coup, ça rendrait

Pour quelle raison ne faut-il pas considérer le temps de propagation en RR ?

[Zefram Cochrane]

Salut pour l'automobile de Poincaré qui correspond à votre schéma, 2∆t' est une durée propre IE mesurée par une horloge et ∆t est une durée coordonnée dans R IE mesurée par deux horloges synchronisées l'une en A lors de l'émission et l'autre en A lors du retour du signal réfléchi. Pythagore suffi pour retrouver le facteur de Lorentz.

[Zefram Cochrane]

Si on peut considérer le temps de propagation. Si on n'avait pas le droit on serait incapable de décrire ce qu'un observateur voit réellement. Ce serait vraiment très embêtant.

[invite6c093f92]

Pour quelle raison ne faut-il pas considérer le temps de propagation en RR ?

A cause de la simultanéité ( ie la synchronisation qui est une convention) qui est toujours calculée, puisque la théorie pose une vitesse limite à l'information. On observe les instants d'arrivée des signaux, et on reconstruit ( par calcul) les instants de départ avec des hypothèses sur la distance ect... La simultanéité est donc non physique, juste dépendant du choix de système de coordonnées.
C'est (pour l'analogie) comme en électro/magnétostatique, on ne prends pas en compte le temps requis pour la propagation d'une modification de la distribution des charges (c'est pour donner l'idée).

[fabio123]

Ah dans ce cas-là, il n'y a plus de problème, je pensais qu'il fallait en tenir compte. Du coup, ça rendrait

Pour quelle raison ne faut-il pas considérer le temps de propagation en RR ?

Je mets un schéma un peu plus explicite concernant les points A, A', B' et B :



@Zefram Cochrane Petite rectification : comme tu dis, il faut prendre comme convention les points A (dans le référentiel R) et A' (dans le référentiel R') qui sont confondus lors de l'émission du photon en A=A' vers le point B'. Ce que j'appelle l'observateur dans (R) sur la gauche correspond à celui qui est situé à A=A' : pour simplifier, l'émission se fait à . Ensuite, une fois que le photon arrive en B' (dans R'), je considère qu'il s'est écoulé dans (R') depuis l'émission en (B') un intervalle

Mais pour les 2 observateurs dans (R) (le premier situé en A=A') et le second (point B, situé au bas de la verticale du point B'), il s'est écoulé . D'un autre coté, Il faut tenir compte du temps de propagation du point B' (dans R') vers le point à sa verticale (qui est le segment L), c'est-à-dire le point (B) : ce temps de propagation entre le point B' et B est égal à .

Je tiens à préciser ici que, excepté pour le décalage entre les point B' et B, je ne tiens pas compte des décalages entre les référentiels (R) et (R') puisque j'ai pris pour simplifier les 2 référentiels dans le même plan (Oyz) et avec A=A' au moment de l'émission du photon vers B'.

Maintenant, le triangle rectangle ne peut être conçu que dans la reconstruction de ce qui s'est vraiment passé entre les 2 évènements " évènement A = émission du photon en A=A' " et " évènement B' = réception au point B' du photon émis en A=A' : l'observateur B qui est au bas de la verticale du point B' recevra ce photon avec un décalage supplémentaire égal à .

Donc, l'intervalle qui s'est vraiment écoulé dans (R), d'une certaine manière "au plus près du train mobile mais toujours dans (R) ", est égal à : puisqu'on prend pour simplifier

Dans ce cas là, je ne retrouve pas avec Pythagore la relation :

car

Les remarques de Zefram Cochrane et didier941751 semblent ne pas être les mêmes : l'un me dit qu'il faut tenir compte du temps de propagation entre les référentiels et l'autre que non.

[fabio123]

Ensuite, une fois que le photon arrive en B' (dans R'), je considère qu'il s'est écoulé dans (R') depuis l'émission en (B') un intervalle

je voulais dire :

Ensuite, une fois que le photon arrive en B' (dans R'), je considère qu'il s'est écoulé dans (R') depuis l'émission en (A') un intervalle

[invite6c093f92]

Les remarques de Zefram Cochrane et didier941751 semblent ne pas être les mêmes : l'un me dit qu'il faut tenir compte du temps de propagation entre les référentiels et l'autre que non.

Bah, tout dépend du point de vue, ici, il me semble que le "point central" ici est un doppler, c'est une façon de faire "à l'ancienne", critiquable (mais il y en a qui aime...Moi non...) car ne parle pas de la représentation (comme dans les cours modernes) quadrivectorielle de l'espace-temps de Minkowski, avec le doppler on apprend à se servir des TL, picétout...(avec les problèmes inhérents à cette "compréhension moins complète", et donc la multiplication des erreurs futures du à ce manque...ZF peut t'en parlerSans aucune méchanceté dans cette remarque, juste de l'humour.