Idées reçues sur les trous noirs

[Amanuensis]

Il n'y a pas de "distance propre" pour un trajet lumineux.
-----

[Mailou75]

Certes, tout ceci est en coordonnées (r;t) de l’observateur a l’infini et c’est de son espace (propre et rigide) dont il est question.
Les durées valent aussi pour lui (j’ai répété «pour l’obs a l’infini» autant de fois que possible..)
Je me trompe ?

[Amanuensis]

Utiliser "propre" est alors se tromper. Faut choisir, soit dire «pour l'obs à l'infini» (qui n'existe que mathématiquement, allusion à autre fil), soit dire "propre", mais pas l'un pour l'autre.

[Zefram Cochrane]

Certes, tout ceci est en coordonnées (r;t) de l’observateur a l’infini et c’est de son espace (propre et rigide) dont il est question.
Les durées valent aussi pour lui (j’ai répété «pour l’obs a l’infini» autant de fois que possible..)
Je me trompe ?

Salut,
Nous savons calculer la longueur propre d'une corde tendue radialement entre deux points fixes d'un champ de graviitation.

est une vitesse coordonnée, pas de la "vitesse propre" (entendons par la que vitesse propre ; et non la célérité ).
Localement, la vitesse de la lumière est constante mais globalement pas. Donc effectivement, nous pouvons expliquer l'effet Shapiro comme étant la conséquence de la vitesse coordonnées de la lumière dans un champ de gravitation et pourquoi la lumière ne peut s'achapper d'un TN ( la vitesse coordonnée est nulle en Rs)
Nous avons déjà distingué la "vitesse propre" de la vitesse coordonnée dans le cadre de la chute libre:
https://forums.futura-sciences.com/a...ml#post4472312

[Mailou75]

Salut,

Nous avons déjà distingué la "vitesse propre" de la vitesse coordonnée dans le cadre de la chute libre:

Merci pour ce rappel. Ce que tu dis confirme une partie de la question, il s’agit bien de l’effet dit Shapiro. L’ennui n’est que ça confirme aussi l’autre point (et c’etait le but de mon post) : si rien ne peut s’echapper d’un TN pour cette raison alors rien n’y entre non plus !?

[Amanuensis]

rien n’y entre non plus !?

Rien n'entre dans un trou noir (1) en coordonnées (t, r) de Schw. Rien de neuf. C'est le système de coordonnées qui est en cause. Rien de neuf.

(1) Au sens aucune ligne causale n'atteint l'horizon

[Mailou75]

Rien n'entre dans un trou noir (1) en coordonnées (t, r) de Schw. Rien de neuf. C'est le système de coordonnées qui est en cause. Rien de neuf.
(1) Au sens aucune ligne causale n'atteint l'horizon

Oui, c’est effectivement ce que disent et ont toujours dit ces coordonnées et c’est un modèle applicable pour tout observateur eloigné, a fortiori pour celui qui est à des milliards de millards de Rs, nous... Mais ce n’est pas ce qu’on entend, on nous parle d’une frontière à sens unique dont rien ne sort mais tout y entre inexorablement.

- soit on applique les coordonnées aux deux horizons (t=+/-oo) est si rien ne sort rien n’y entre
- soit on admet que si l’observateur ne voit rien de ce qui se passe «de façon normale» aux alentours de Rs c’est à cause des déformations de l’espace temps, valables dans le futur (frontiere avec II) et dans le passé (frontière avec IV, trou blanc ??). Il peut donc y avoir des rayons qui sortent du trou noir mais on ne peut pas les voir, qu’ils aient été émis dans le passé, le présent (un t0 arbitraire) ou le futur n’y change rien.

Candidature pour une nouvelle «idée reçue»

Mailou

[Zefram Cochrane]

Salut,
Ce que montre ton schéma est que la vitesse coordonnée est une vitesse apparente du chuteur pour l'obs à l'oo qui tombe à zéro pour tout observateur externe, la vitesse propre du chuteur est une vitesse calculée par le chuteur et si elle est inférieure à c au passage de Rs c'est parce que le chuteur poursuit sa chute vers la singularité.
Mais l'observateur externe ne le verra jamais chuter dans le TN, (*)

C'est le même principe que l'horizon des événement avec Rindler :
Si à T=0s , un observateur s'éloigne d'une station (genre étoile noire) situé à 30Ms.l avec une accélération propre g° = 10m/s² et que la station tire un faisceau laser destrecteur vers la la navette de l'observateur à T=0s, la navette tant qu'elle accélèrera à minima à g° ne sera jamais détruite par ce que l'observateur verra l'horloge de la station tendre vers 0s mais ne la verra jamais afficher 0s.
de la même manière il ne verra jamais le faisceau laser détruire les bouées situées toutes les s.l sur la trajectoire de la navette afficher successivement (1s; 2s;3s;...s) ; pourtant les bouées seront détruites à
(1s; 2s;3s;...s)

En RG c'est un peu pareil parce que les bouées serait en chute libre tandis que l'observateur serait stationnaire par rapport à l'horizon des événéments.

(*) en ne tenant compte que des données cinématiques

[Amanuensis]

, la vitesse propre du chuteur est une vitesse calculée par le chuteur

Comment? Sur la base de quelles observations qu'il peut faire?

[Pour moi, c'est une «vitesse» calculée par Zefram Cochrane observant les équations...]

[Amanuensis]

- soit on admet que si l’observateur ne voit rien de ce qui se passe «de façon normale» aux alentours de Rs c’est à cause des déformations de l’espace temps,

Partiellement. Il y a aussi des contraintes de causalité.

Il peut donc y avoir des rayons qui sortent du trou noir

Non, pour raisons causales, pas seulement de «déformation de l'espace-temps» (WTM).

De même pour l'horizon passé, rien n'y entre pour raisons causales.

[Zefram Cochrane]

Comment? Sur la base de quelles observations qu'il peut faire?

[Pour moi, c'est une «vitesse» calculée par Zefram Cochrane observant les équations...]

Salut C'est plutôt un travail colaboratif
https://forums.futura-sciences.com/a...ml#post4410433

et est ce qui permet d'affirmer qu'un chuteur en chute libre depuis une coordonnée Ro finie atteindra l'horizon avec une vitesse inférieure à c.

[Amanuensis]

Cela ne répond pas à la question.

[Amanuensis]

et est ce qui permet d'affirmer qu'un chuteur en chute libre depuis une coordonnée Ro finie atteindra l'horizon avec une vitesse inférieure à c.

La vitesse (coordonnée) est inférieure à c du seul fait qu'il suit une ligne d'univers.

[Zefram Cochrane]

Cela ne répond pas à la question.

Voici les calculs :
https://forums.futura-sciences.com/a...ml#post5139749
Pour répondre à ta question :
il peut déterminer la vitesse en mesurant la célérité ie localement la longueur de règle stationnaire parcourue en une durée propre infinitésimale.

[Amanuensis]

localement la longueur de règle stationnaire parcourue en une durée propre infinitésimale.

Et comment il mesure cette longueur? (Jamais entendu parler de la contraction des longueurs?)

[En fait Zefram Cochrane a mis au préalable des bornes kilométriques sur le passage de l'observateur, marquées «borne stationnaire» avec l'indication de la valeur de r... Avec des moteurs fusée pour qu'elles restent «stationnaires».]

[Zefram Cochrane]

Et comment il mesure cette longueur? (Jamais entendu parler de la contraction des longueurs?)

[En fait Zefram Cochrane a mis au préalable des bornes kilométriques sur le passage de l'observateur, marquées «borne stationnaire» avec l'indication de la valeur de r... Avec des moteurs fusée pour qu'elles restent «stationnaires».]

Avec l'effet Doppler transverse, il peut connaître donc donc
Par exemple en faisant clignoter une guirlande avec des loupiottes mochromatiques dont la couleur à l'émission est connue et en ragardant sa couleur lorsqu'on passe à son niveau.

[Amanuensis]

Par exemple en faisant clignoter une guirlande avec des loupiottes mochromatiques dont la couleur à l'émission est connue et en ragardant sa couleur lorsqu'on passe à son niveau.

Ah,, OK. Ce ne sont pas des bornes kilométriques, mais des guirlandes qui ont été posées au préalable. (Avec des moteurs fusée, toujours pour rester stationnaire.)

Trêve de plaisanterie: ce qui est mesuré est la vitesse de certains objets qu'on sait (par quel moyen?) être immobiles relativement au référentiel de Schwarzschild. Le décalage de fréquence est traduit en une vitesse par la formule du doppler relativiste. C'est ça?

[Mailou75]

Salut,

(...) si elle est inférieure à c au passage de Rs c'est parce que le chuteur poursuit sa chute vers la singularité.

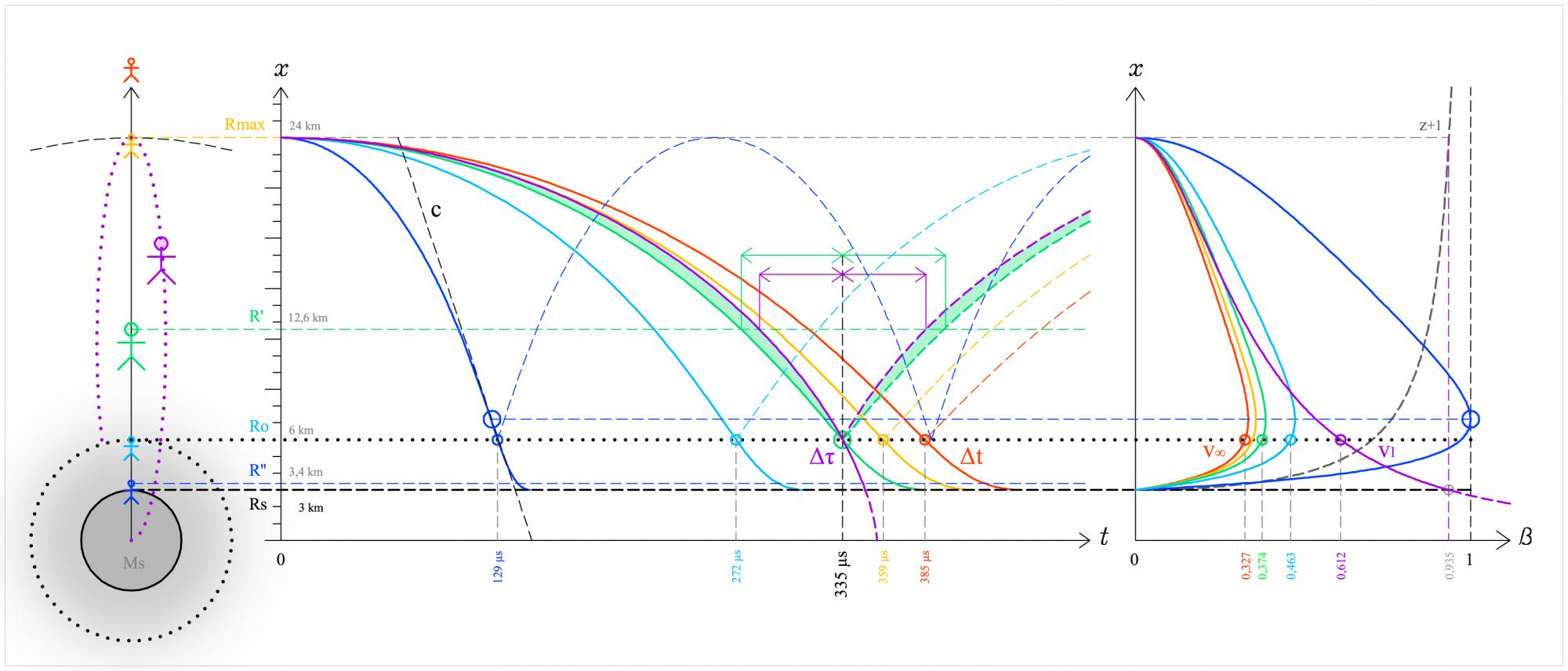
Si elle est inferieure à c c’est simplement que le voyageur et parti de moins loin que l’infini... si l’effet Einstein vaut z+1 à l’altitude de départ en chute libre (vitesse initiale nulle) alors sa vitesse au passage en Rs vaut (z+1)c. NB : z+1=1 à l’infini

En RG c'est un peu pareil parce que les bouées serait en chute libre tandis que l'observateur serait stationnaire par rapport à l'horizon des événéments.

Non, c’est plutot comme si tu te mettais dans le repère de chaque nouvelle bouée au passage du lazer. Tu obtiendras systématiquement la même trajectoire hyperbolique pour un accéléré. De la même façon, un changement de répère en KS se fait par rotation hyperbolique et modifie t0. La grande différence c’est que Rindler tourne autour de l’évènement (0;0) alors que KS modifie le centre (Rs;présent), passé et futur étant totalement arbitraire chez KS.

..........

Partiellement. Il y a aussi des contraintes de causalité.
(...)Non, pour raisons causales, pas seulement de «déformation de l'espace-temps» (WTM).
De même pour l'horizon passé, rien n'y entre pour raisons causales.

Passé, futur, pour moi c’est le même horizon... je ne vois pas trop en quoi le choix d’un t0 pour la figure pourrait en modifier les propriétés. Et puis l’effet Shapiro c’est un truc qu’on a pu mesurer, les GPS aussi... Il est donc bien question de retranscrire tous les effets de la RG dans un plan rigide euclidien qui decrit «ce qui sera vu de ce qui se passe dans cet espace» (potentiellement observé par un cone passé droit Minkowskien) et c’est purement et simplement ce que fait Schw.

........

Comment? Sur la base de quelles observations qu'il peut faire?

Par n’importe quel observateur (ou le voyageur lui même) qui le voit parcourir dr (effectivement les bornes c’est pas mal pusqu’on ne sait toujours pas décrire ce qu’on voit pour quiconque... humm) pendant une durée dT de la montre du voyageur. Il est nécessaire que la formule de Zef soit bonne puisque tout en découle : Painlevé c’est Newton (ou Zef) avec des vitesses possiblement suppérieures a c à l'intérieur, et pour passer en Scwh on ajoute z+1 et gamma applicables dans l’espace rigide decrit plus haut pour passer de T à t. (Ben oui moi aussi je trouve ca un peu fake mais c’est un fait...)

Mailou

[Zefram Cochrane]

Ah,, OK. Ce ne sont pas des bornes kilométriques, mais des guirlandes qui ont été posées au préalable. (Avec des moteurs fusée, toujours pour rester stationnaire.)

Trêve de plaisanterie: ce qui est mesuré est la vitesse de certains objets qu'on sait (par quel moyen?) être immobiles relativement au référentiel de Schwarzschild. Le décalage de fréquence est traduit en une vitesse par la formule du doppler relativiste. C'est ça?

C'est le principe en effet.

Pour le moyen :
J'imaginais plus une station spatiale stationnaire au dessus du champ de gravitation à la coordonnée Ro et dont les occupants ressentent les effet d'une accélération propre
(tu confirmes la formule?); il sont donc capables de savoir s'ils sont stationnaires dans le champ de gravitation.
De la station on déroule radialement la guirlande de longueur propre L et de la même manière mesurer le poids de masse test pour calculer la coordonnée R au niveau de chaque lampe.
Comme on sait calculer cette longueur propre L on peut théoriquement dérouler la guirlande jusqu'à ce qu'on extrémité éfleure l'horizon du TN.

[Mailou75]

Salut,

(il faudrait que je vérifie si ça correspond simplement au ralentissement local du temps..?)

C'est chose faite et bien sur ça a tout à voir ! Voilà comment j'interprète le Kruskal

La figure est supposée donner des rapports qui sont justes de façon infinitésimale mais elle ne l'est pas... elle est donc entachée d'imprécision mais pas tant que je le pensais (ça joue surtout sur Rouge et encore) et suffisante pour saisir le problème. Les unités d'espace sont toujours en Rs et les unités de temps en Rs/c.

Description pour Vert, stationnaire à r=1,9Rs (valable pour les autres)

Pour l'observateur à l'infini, Vert est vu avec un redshift gravitationnel (effet Einstein) z+1=1/rac(1-Rs/r) ~ 1,453
Donc lorsque l'observateur à l'infini compte 1,309 Vert compte 1,309/1,453 ~ 0,9 (Rouge 0,7 et Bleu 1,0)
Pour l'observateur à l'infini la lumière met un temps t ~ 0,423 pour aller de 2Rs à 1,8Rs (ou de 1,8 à 2 c'est pareil)

Pour Vert, localement, la distance comprise entre 2Rs et 1,8Rs vaut d = 0,2*1,453 ~ 0,291
(distance propre "arpentable" vérifiée avec une autre formule trop chiante à écrire en latex...)

Le KS montre que pour lui, la lumière met un temps (propre) de 0,423/1,453 ~ 0,291 donc tout va bien localement !
(on peut voir que la diagonale t=0,423 croise la trajectoire de Vert juste en dessous du troisième point T=0,3)

Pour que tout ceci fonctionne il faut que l'observateur à l'infini voie la scène au ralenti et compressée :
- la distance propre locale est vue compressée 0,291/1,453 = 0.2 Rs
- le temps propre local est dilaté 0,291*1,453 ~ 0,423 Rs/c

Pour lui, la lumière ralentis aux alentours de 1,9Rs, elle parcourt 0,2Rs en 0,423Rs/c soit une vitesse apparente c' = c / (z+1)²
(qui correspondrait à la formule de Zef)

Il faut donc se méfier des valeurs d'espace cotées, de Bleu à Rouge car :
- X est de plus en plus petit
- r est constant
- d (valeur sur la flèche) est de plus en plus grand

Voilà, j'aimerais déjà savoir si tout ceci est juste avant de passer à la suite...
on va peut être enfin savoir comment sont vues les choses radialement !

Merci d'avance

Mailou

[viiksu]

"D'où la double question suivante : Ceci traduit-t-il il le ralentissement de la lumière à proximité d'un masse (effet Shapiro) ET, si c'est le cas, peut-on dire qu'un rayon parti de 4Rs (au pif) n'arrive jamais en Rs ? "

Est-ce que ça ne dépend pas du point de vue. Pour un observateur près de Rs ou qui tombe le rayon lumineux franchit Rs, pour un observateur au loin rien ne pénètre le TN.

[viiksu]

C'est assez marrant d'ailleurs pour nous rien ne pénètre jamais dans le TN seul son disque d'accrétion est visible ce qui s'approche du TN disparaît à notre vue par effet Doppler relativiste et /ou Shapiro c'est tout.

[Mailou75]

Salut,

Est-ce que ça ne dépend pas du point de vue. Pour un observateur près de Rs ou qui tombe le rayon lumineux franchit Rs, pour un observateur au loin rien ne pénètre le TN.

Et suivant la logique definie dans ce fil si un rayon peut entrer c’est qu’un autre peut sortir... Ça fait longtemps que je caresse l’illusion que le rayon du trou noir dépend de la position (et du mouvement eventuel) de l’observateur. La vitesse de liberation nous dit qu’un solide arrive à l’infini avec une vitesse nulle, par analogie un photon quittant radialement un trou noir arrive à l’infini avec une fréquence nulle (diminution d’energie sans perte de vitesse) et ne peut donc etre vu. Quid d’un observateur qui n’est pas à l’infini, voit-il un photon de fréquence diminuée mais non nulle ? En l’état ce n’est pas ce que disent les formules, mais on peut essayer de les faire parler... Pour l’heure la question est un peu anticipée, j’essaye de prendre du «recul» et comprendre ce que dit Schw à l'extérieur et pas forcément pour un trou noir (les derniers schémas valent pour une étoile a neutron de 1,3Rs par exemple). Question interessante donc mais à laquelle je n’ai pas encore de réponse solide

A bientot

Mailou

[Mailou75]

Illustrons ceci :

- X est de plus en plus petit
- r est constant
- d (valeur sur la flèche) est de plus en plus grand

On va s'intéresser à ce qui est vu, et pour ça il va falloir regarder du coté des cônes passés

1/ Kruskal

Le haut du schéma reproduit les valeurs données dans mon dernier message, suite...

Pour savoir comment l'observateur à l'infini voit les choses il faut faire une petite bidouille : on voit qu'au delà de 2,6Rs l'axe d'espace est sectionné et on arrive directement à l'infini (alors que c'est la position d'un immobile à 2,9Rs). On montre donc les évènements vus par celui à 2,9Rs mais avec le temps propre de l'observateur à l'infini, car ce qui nous intéresse c'est l'intervalle de réception. Pas très catholique mais ça marche...

Les cônes passés jaunes confirment que l'observateur à l'infini (Gris) perçois les bons intervalles de temps pour des longueurs parcourues de r=0,2Rs :
- 0,343 entre 2,3 et 2,5Rs
- 0,423 entre 1,8 et 2Rs
- 0,711 entre 1,3 et 1,5Rs
NB : Je n'ai pas mis les - pour les valeurs négatives.

La nouveauté c'est ce que voit Vert. Poursuivons la même logique que pour l'observateur à l'infini, avec en prime que ce sont les bons évènements vus.

Vert estime que le temps que met la lumière pour aller de 1,3 à 1,5Rs est de 0,481.
Il voit Rouge avec un redshift gravitationnel z+1=1,871/1,453 ~ 1,287 (~ 9/7)
Il voit la distance propre d=0,374 compressée à la valeur qu'il donne lui même à un intervalle de 0,2Rs soit 0,374/1,287 ~ 0,291
Il voit le temps propre de Rouge ralenti de z+1 soit 0,374*1,287 ~ 0,481, ce que montre KS.
Il voit donc la lumière parcourir 0,291Rs en 0,481Rs/c il estime donc qu'aux environs de 1,4Rs la lumière va à c'=c * (z+1)², comme pour Gris.

Vert estime que le temps que met la lumière pour aller de 2,3 à 2,5Rs est de 0,236.
Il voit Bleu avec un blueshift gravitationnel z+1=1,309/1,453 ~ 0,901 (~ 9/10)
Il voit la distance propre d=0,262 dilatée à la valeur qu'il donne lui même à un intervalle de 0,2Rs soit 0,262/0,901 ~ 0,291
Il voit le temps propre de Rouge accéléré de z+1 soit 0,262*0,901 ~ 0,236, ce que montre KS.
Il voit donc la lumière parcourir 0,291Rs en 0,236Rs/c il estime donc qu'aux environs de 2,4Rs la lumière va à c'=c * (z+1)², c' > c cette fois !

La logique pourrait donc être la bonne
La compression dilatation des longueurs peut être comprise chez KS comme une analogie avec les accélérés de Rindler (https://forums.futura-sciences.com/a...ml#post6151725) mais on ne peut pas se permettre de projeter le cône passé sur l'axe X car celui ci n'a rien d'une longueur propre.


2/ Schwarzschild

Finalement le top pour décrire ce qui est vu c'est notre pote Karl ! Il donne directement l'intervalle en multiple de Rs comme il sera vu par n'importe lequel des observateurs. Pour l'observateur à l'infini on ne change rien, c'est son repère. Evidement, comme déjà dit, la bidouille faite ici fait que ce ne sont pas les bons évènement mais c'est le bon intervalle et Gris verra entre deux cones passés les temps propres de Rouge, Vert et Bleu varier par rapport au sien, et entre eux, tout en restant sur place.

Pour les autres c'est très simple, on dilate horizontalement la figure du facteur z+1 de l'observateur. Par exemple pour Vert on étire la figure jusqu'à ce que r=0,2Rs mesure d=0,291Rs. Ensuite on a le droit de projetter le cône passé sur l'axe horizontal, pas parce que c'est devenu une longueur propre, mais parce que c'est directement ce qui est vu, y compris les bons évènements.

Ensuite on peut dilater la figure de façon non uniforme de manière à ce que r devienne d, je l'ai faite comme transition mais elle n'a pas grand intérêt, je ne l'ai pas montrée. Je suis passé directement à l'étape suivante...


3/ Flamm

Je l'ai nommé Flamm car d est la longueur d'une corde rayonnante tendue sur la surface d'un paraboloïde de Flamm.
Le profil de révolution est donné par y=2*rac(Rs(r-Rs)) mais la longueur de la corde est (cette fois je m'y colle) pour r > Rs

longueur finie...

On peut donc inventer un système dans lequel l'axe soit une longueur propre locale partout dite "arpentable", reste à savoir ce qu'on fait de t... et bien pour que le repère soit exactement Minkoskien en tout point de d il faut noter sur l'axe de temps ! Le temps propre est alors le même pour toutes les trajectoires de Rouge, Vert et Bleu. Evidement Gris, comme il n'est pas à sa place, à l'infini, doit s'adapter... L'espace n'évolue alors plus le façon parallèle mais retrouve un point fixe en Rs comme chez Kruskal. Vous noterez que la figure démarre à Rs, conformément à la définition de d.

On obtient donc un système où partout localement à t=0 (cad sur l'axe d) l'espace temps est Minkoskien : les cônes passés sont à 45°, l'espace est une longueur propre et la durée est un temps propre. Evidement dès qu'on s'écarte un peu de t=0 c'est la foire...

Pour moi ce graph traduit le fait que Rs est toujours un point à t=0, au présent. Que sur les autres graphs, la droite pointillée représente toutes les positions Rs à toutes les dates. On y écrit t=+/-oo chez Kruskal parce que c'est la date à laquelle un photon doit partir de Rs pour être vu à t=0 par quiconque. Ici on voit clairement que pour faire un changement de repère il faut déplacer le point au t=0 suivant/précédent et que toutes les courbes risquent d'être fortement distordues !

Pour finir, vous remarquez la similitude de la forme du cône passé "en poire" avec celui de la cosmo, avec sa "singularité passée", moyennant qu'on prenne l'axe d'espace pour un axe de temps... humm hors sujet et non réfléchi.

Voilà, donc si tout ceci est juste (j'aimerais bien une petite confirmation svp) on a peut être un moyen "facile" de représenter ce qui est vu et surtout comment c'est vu ! (Schwarzschild)

Bonne lecture et merci d'avance pour vos réponses

Mailou

[Mailou75]

Bonsoir,

Soit je suis en train d’énoncer des faits évidents pour chacun, soit j’ai fini par comprendre à ma façon ce que cachaient les équations à mes yeux. Dans tous les cas ce qui est décrit est une simple règle de proportionnalité, pas des maths de haute voltige, et ceux qui ont compris cette «métrique» devraient pouvoir rapidement juger de la justesse ou non de mes calculs. Une autre possibilité est que ce soit faux, dans tous les cas je suis assez etonné de ne lire aucune réponse. La dernière possibilité est que le sujet n’interesse personne, mais ce n’est pas l’impression que j’avais... Je finirais bien de répondre à la question initiale par quelques dessins plus parlants mais je ne voudrais pas partir sur de mauvaises bases. Je demande donc à ceux qui ont la capacité à le faire de bien vouloir critiquer mon dernier message.

Merci d’avance

Mailou

[mach3]

Il semble que la démarche ne s'appuie pas sur les bons concepts et/ou s'appuie sur des concepts non compris. Cela la rend très difficile à suivre. Par exemple, quand il est question de distance propre, on ne comprend pas bien ce que ça désigne dans le contexte. Quand il y a une bidouille pour que l'observateur à 2.9rs soit celui à l'infini, on ne comprend pas pourquoi ni d'où ça sort. En gros on ne va même pas au bout du message vu qu'au bout de même pas un quart on n'est même pas sûr de comprendre.

m@ch3

[viiksu]

Désolé Lauloi mais je n'ai pas le niveau par contre je garde au chaud ces discussions très intéressantes.

[Amanuensis]

Comme Mach3, je n'ai pas trop de temps à consacrer à des présentations utilisant un langage et de concepts par trop «personnel». En principe, c'est à ceux qui écrivent de le faire de manière adaptée aux lecteurs qu'ils visent, pas à ces derniers de jouer au petit Champolion.

Ceci dit, je me demande si au fond il est sujet de l'invariance du quadrivolume lors d'un transport géodésique, ainsi que par transformation de Lorentz, pour une solution du vide (tenseur de Ricci nul).

[viiksu]

Comme d'habitude Amanuensis est intraitable, je trouve remarquable que quelqu'un ait pris le temps d'écrire l'énorme post #114.

[mach3]

Je viens de regarder une vidéo de Science4all sur les maths de la RG que j'ai trouvé plutôt bien faite, ça pourra peut-être servir à mailou (et à d'autres) pour comprendre certaines choses sur le fond (métrique, cristofel, géodésique, riemann, ricci), et coïncidence, à un moment il y a un rapport avec "l'invariance du quadrivolume lors d'un transport géodésique" quand Ricci est nul.

https://www.youtube.com/watch?v=wIx_W-5nGgs

m@ch3