Exercice application loi d'Antoine

[invite5ea89397]

oui, j'avias trouver quelque chose comme cela T0=341,9 mais vu que dans la 1ère ligne du système, on a:
A(1/T0 -1/T)=0, on avais A= 0 ou T0=T a peu près égal à 341,9 K
ou bien faut il trouver la valeur de A via la seconde ligne ?
-----

[petitmousse49]

Tout dépend de ton niveau en math mais franchement, l'approximation est acceptable. Pour ne rien te cacher, la résolution précise du système conduit à To=341,5K...
PS : je viens de terminer les calculs. Par rapport au valeurs proposées sur le site, l'écart relatif ne dépasse pas 3% par excès ou par défaut. Un peu mieux que pour l'eau que j'avais d'abord étudiée !

[invite5ea89397]

globalement, je ne pense pas avoir de grosses difficultés en maths mais je n'aimerais juste pas que cela fausse le sens physique
donc pour résumer, on a donc l'équation suivante:
ln(ps)=ln(p0)+ A*(1/T -1/T0)
et donc ln (ps)= ln (P0) ?
mais dans ce cas, la température n'intervient plus ?

[petitmousse49]

L'équation générale de la courbe Ps=f(T) a été fournie #8. Elle contient deux inconnues A et To. Pour calculer ces deux inconnues, il te faut deux points appartenant à la courbes. Ces deux cas particuliers conduisent au système d'équation fournie message #13.
Pour trouver To de façon rigoureuse, tu peux effectuer le rapport "membre à membre" des deux équations. Cela te fournit un nouvelle équation où A a disparu ; cela permet d'obtenir To (je viens de d'indiquer la valeur). Une fois To connue, remplace To par cette valeur dans la seconde des deux équations pour obtenir la valeur de A.
Tu pourras alors écrire l'expression de Ps en fonction de T sous la forme :

où A et To sont deux constante maintenant connues.
Si tu veux Ps en bar, pose P°=1bar ; si tu veux Ps en mmHg, pose P°=760mmHg.

[invite5ea89397]

ah oui, veuillez m'excusez je n'avais pas fais disparaître le logarithme, je vais donc tout reprendre calmement .....
merci pour votre aide

[invite5ea89397]

alors, voici l’équation que je trouve si je raisonne ne mmHG, je trouve ps=p0*e^(3540,43*(1/341,9- (1/T))
est ce la bonne équation ?

[invite5ea89397]

bonjour, pouvez vous me dire si les résultats trouvé sont correct ?

[RomVi]

Bonjour

Il n'y a aucun sens à régresser Antoine à partir de 2 points, ce serait comme chercher l'équation d'une droite passant par un seul point...
La démarche à adopter et de placer les 2 points connus dans un graphique, avec en abscisse 1/T ou 1000/T (température en Kelvin) et en ordonnée log(P)
La régression est la formule de la droite passant par ces 2 points, en prenant bien évidement les corrections apportées sur chaque axe.

Une petite image pour illustrer : https://upload.wikimedia.org/wikiped...e_of_Water.png

[invite5ea89397]

ah oui, très bonne iddée, dans ce cas, il faudrait tracer la courbe avec les points et résoudre, l'équation de la droite en afin de trouver l'ordonnée à l'origine et la pente ?
si c'est le cas, pouvons nous choisir si on la trace en logarhitme ou non ?
pourquoi la tracer en fonction de 1/t?

[RomVi]

Parce que ce n'est qu'à cette condition que les points passent par une droite.
On peut choisir de tracer la courbe en fonction de 1000/t pour une question d'échelle entre les valeurs.

[invite5ea89397]

donc, je trace la droite à la main ou via excell et je cherche pente puis ordonnée à l'origine en fonction des 2 points
est cela ?

[RomVi]

Oui c'est bien ça.

[invite5ea89397]

d'accord
merci beaucoup, je vais faire le calcul et après vous soumettre mes résultats

[invite5ea89397]

si je comprends bien, le graphique sera en échelle semi-log si je décide de le tracer sur excell ?

[invite5ea89397]

le graph doit il être de cette forme

[petitmousse49]

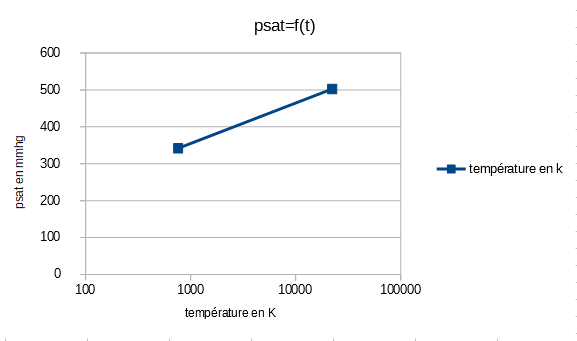
Bonsoir

alors, voici l’équation que je trouve si je raisonne ne mmHG, je trouve ps=p0*e^(3540,43*(1/341,9- (1/T))

C'est effectivement cela.
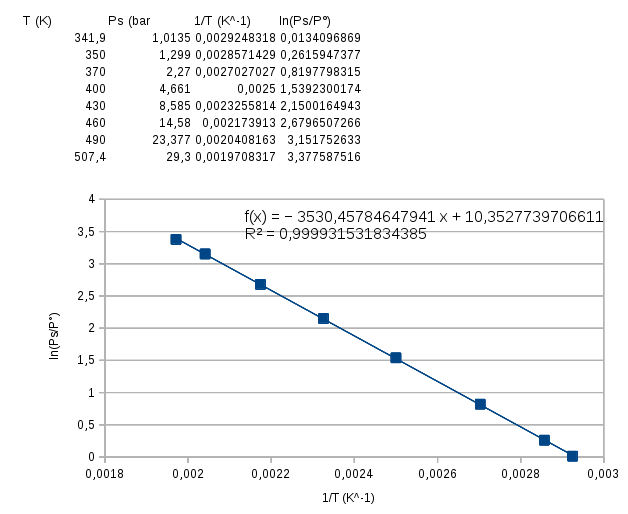
A titre de vérification, comme proposé par Romvi, tu peux, à partir des points expérimentaux que tu trouveras sur le site déjà indiqué, tracer la courbe ln(Ps/P°) en fonction de 1/T.
Tu devrais obtenir des points sensiblement alignés. Un programme de régression linéaire va te donner l'équation de la droite moyenne. Tu devrais obtenir une droite moyenne de coefficient directeur très voisin de -A=-3540K et une ordonnée à l'origine très voisine de (A/To). Je suppose que tu réalises l'étude entre les conditions normales et les conditions critiques.

[invite5ea89397]

oui, je ne suis pas un spécialiste du sujet, mais ça pourrait être intéressant de comparer les courbes et différents paramétres.....
seul problème dans la méthode proposé par RomVi est que je ne suis pas très copain avec les équation de droites faisant intervenir du semi log
pourriez vous m'aider à déterminer la pente et l'ordonnée à l'origine
et sur excel je peut donc tracer la courbe avec l'équation trouver ?

[petitmousse49]

Si tu n'as pas l'habitude du semi log, tu peux t'en passer si tu sais un peu te servir d'un tableur style Excel.
Dans une première colonne de ton tableur, tu rentres un certains nombres de valeurs de T comprises entre 341,9K et 507,4K. Dans la deuxième colonne, tu entres les valeurs correspondantes de Ps en bar prises sur le site dont je t'ai parlé. Troisième colonne, tu fais calculer à l'ordinateur les valeurs de 1/T ; 4ième colonne : tu fais calculer les valeurs de ln(Ps)=ln(Ps/P°) si Ps est en bar.
Il te suffit alors de faire placer dans un repère les points d'abscisses (1/T) et d'ordonnées ln(Ps). Tu traces la droite moyenne et tu demande l'obtention de l'équation de la droite moyenne (le tableur possède un programme de régression linéaire). Tu devrais logiquement obtenir des résultats très proches de ceux évoqués dans mon message précédent.

[invite5ea89397]

pas de soucis, je vais alors de ce pas aller essayer
merci beaucoup pour votre aide

[petitmousse49]

Juste par curiosité, j'ai testé la méthode que je t'ai expliquée dans le message #48. Outre les valeurs correspondant aux conditions normales et aux conditions critiques fournies par ton énoncé, j'ai ajouté un certains nombres de valeurs obtenues sur le site déjà cité, valeurs qu'il est possible je pense de considérer comme fiables. Les points peuvent en excellente approximation être considérés comme alignés, ce que prouve la valeur de R² très proche de 1. L'équation de la droite moyenne conduit à A=3530K et à To=(3530/10,353)=341K.
La résolution rigoureuse du système de deux équations à deux inconnues que je t'ai précédemment fourni conduit à : A=3526K ; To=341K. Tout cela est parfaitement cohérent compte tenu des incertitudes sur les mesures. Tu peux donc je pense, sur l'intervalle de températures considéré, valider l'équation :

PS : Un titre à cette discussion du genre : "modélisation de la courbe d'équilibre liquide - vapeur de l'hexane", sans référence à l'hypothèse très hasardeuse et au final fausse de la loi d'Antoine, aurait sûrement évité bien des confusions...