La Théorie de l'éther de Lorentz implique t'elle la relativité de la simultanéité?

[Zefram Cochrane]

Bonjour,
On attribue à la LET une simultanéité absolue mais il semblerait que ce soit faux; c'est ce que je cherche à confirmer.
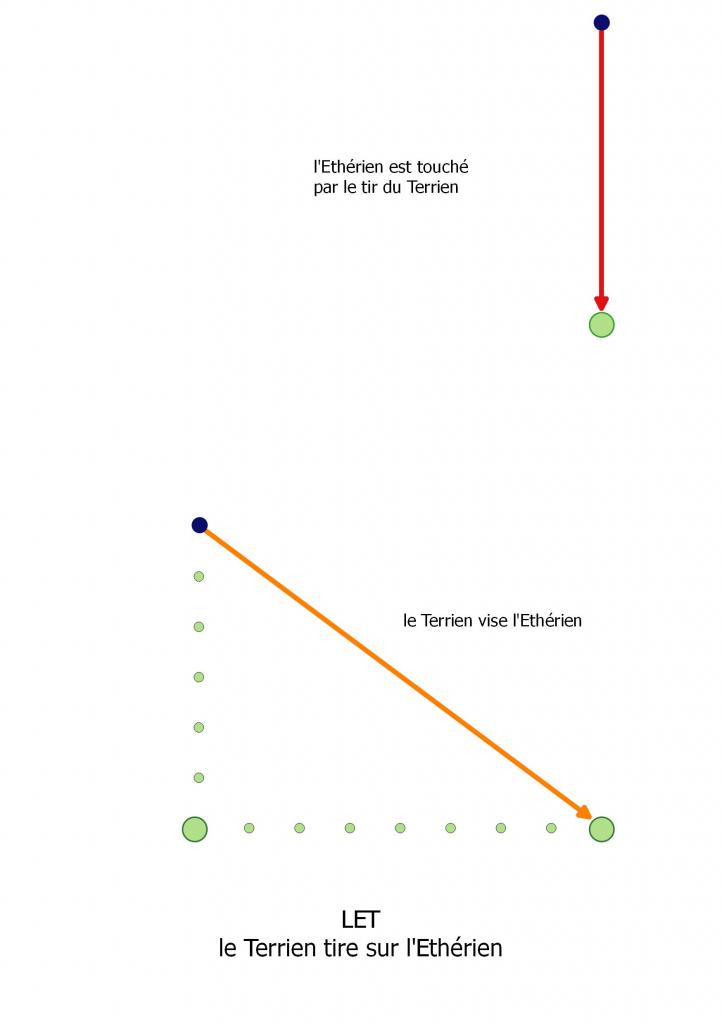
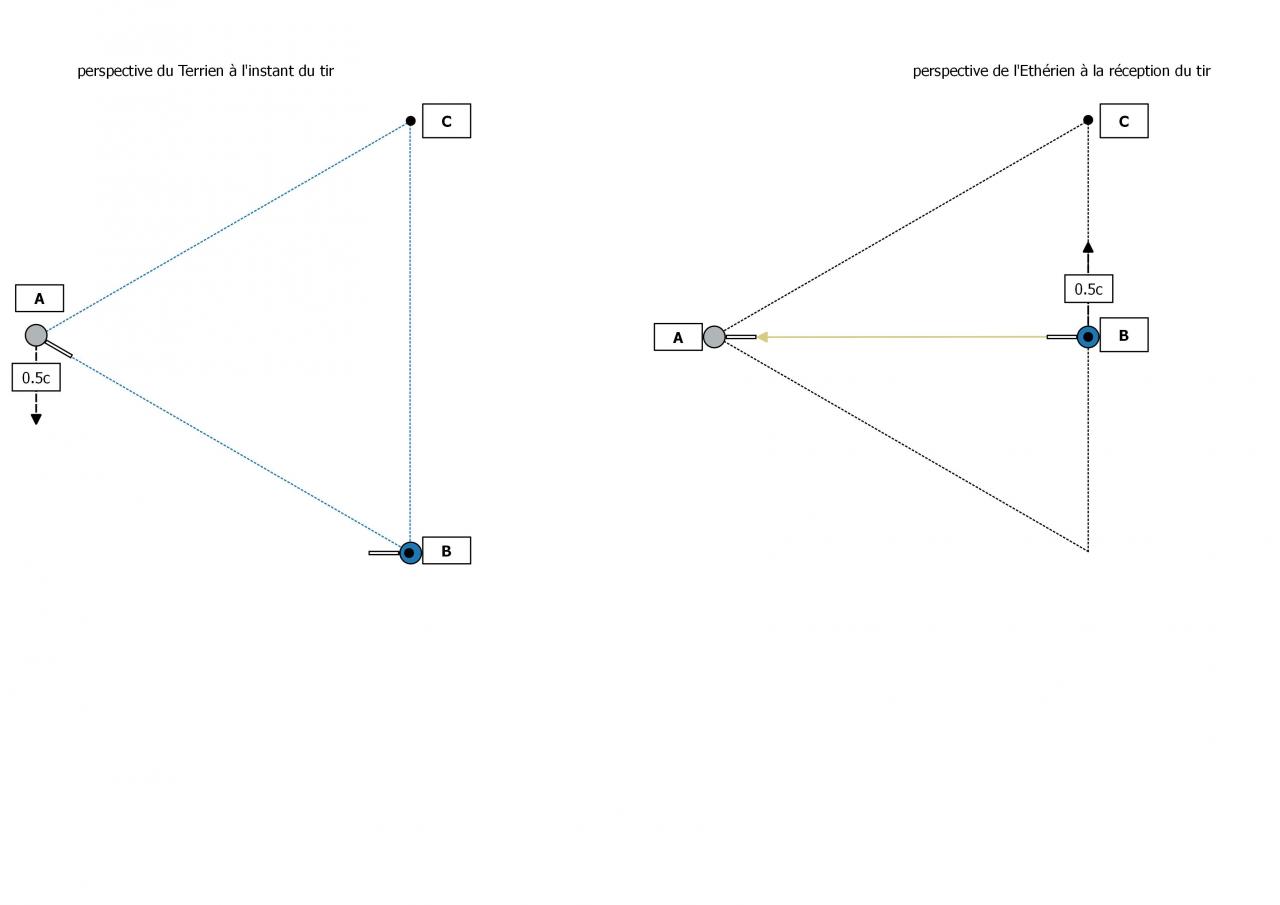
Soit une source (l'émetteur) dans un référentiel inertiel K' en MRU à v=0,8c par rapport au récepteur situé dans référentiel le référentiel de l'éther.
.............................. ...............
Avec la LET on postule que :
1) la vitesse est anositrope dans le référentiel K'
2) (dilatation du temps) que le temps s'écoule Y=5/3 fois moins vite dans K' que dans le référentiel de l'éther: t = Y * t'
3) (constraction des longueurs) que les longueurs sont contractées dans le sens du mouvement d'un facteur Y=5/3 par rapport au longueurs du référentiel de l'éther: l' = Y * l.
Ces conditions sont nécessaires pour être conformes avec l'expérience de Michelson & Morlay et celle de Kennedy & Thorndike.
.............................. ......
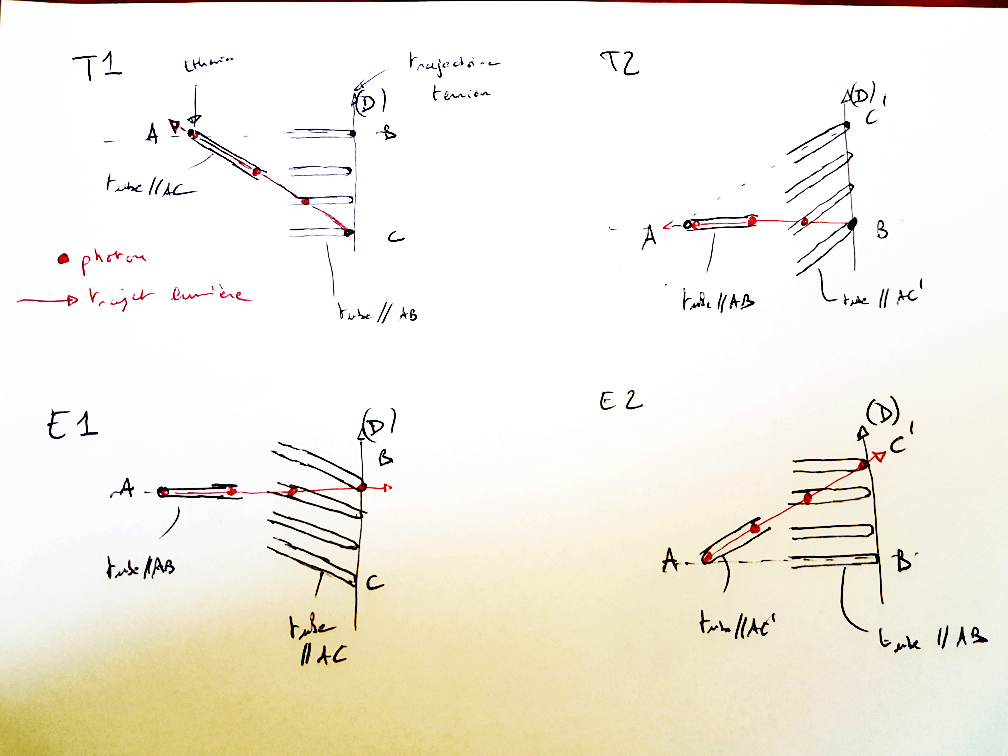
À t = t' =0s une source situé au milieu d'un train de longueur 2l'=10s.l émet deux éclats lumineux en direction des extrémités du train. Du point de vue de O dans le référentiel de l'éther, le train ne mesure que 2l=6s.l du fait de la contraction des longueurs. L'éclat lumineux émis vers l'arrière du train progresse à 1,8c et met, selon O, une durée 1,667s à parvenir jusqu'à un miroir , soit pour O' une durée de 1s; l'éclat lumineux émis vers l'avant du train progresse à 0,2c et met, selon O une durée de 15s pour atteindre le miroir de l'avant du train , soit pour O' une durée de 9s.

Notons que du fait de l'anisotropie de la vitesse de la lumière dans K', les vitesses de progression des éclats luùmineux sont de 0,2c dans le sens du mouvement du train et de 1,8c dans le sens inverse du mouvement du train selon O et O'. Si bien que la durée aller-retour des rayons lumineux est selon O de 10s pour une longueur de 5s.l parcourue. On est donc incapables d'après les expériences de MM et de KT de mesurer qu'elle est la vitesse de O' par rapport au référentiel de l'éther.
..........................
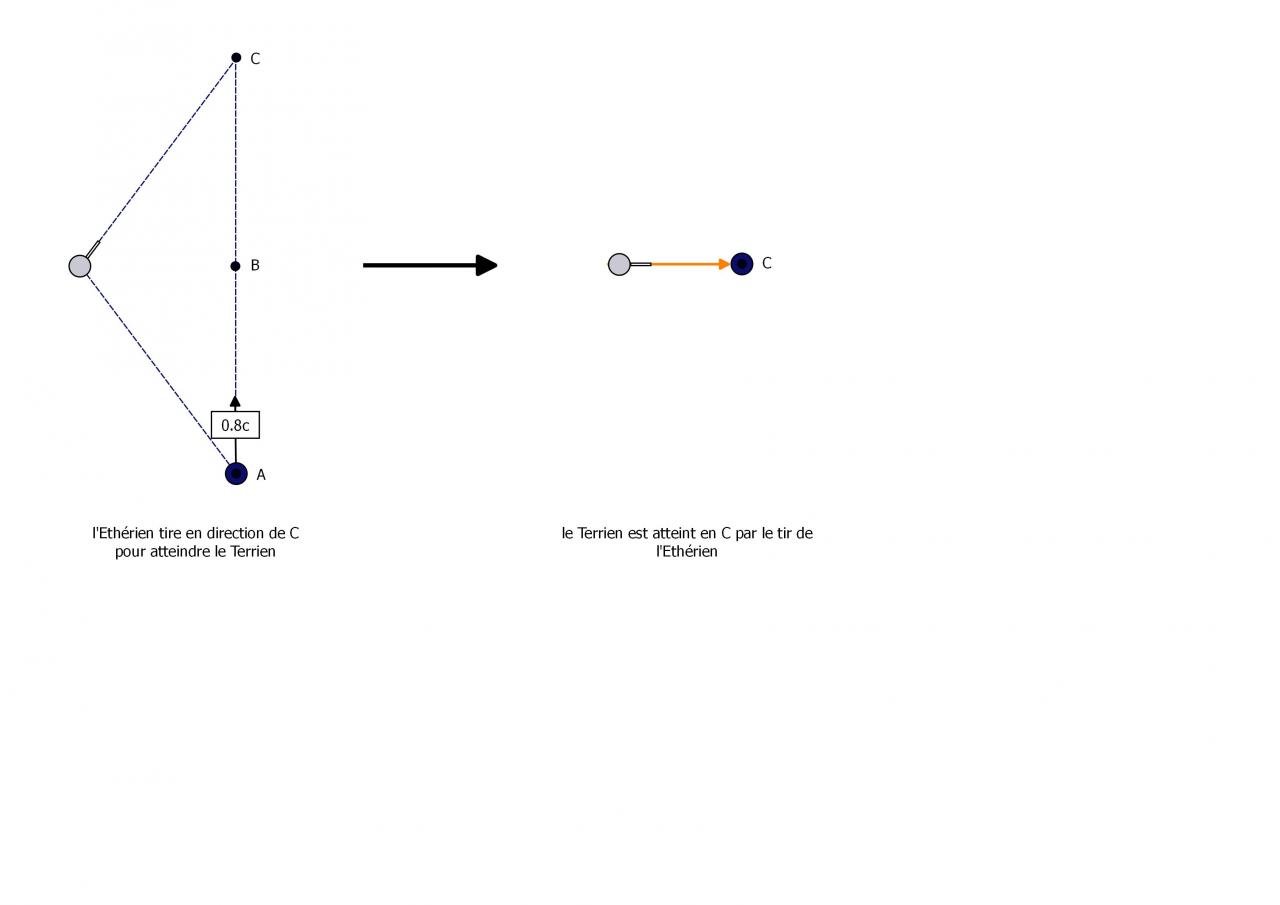
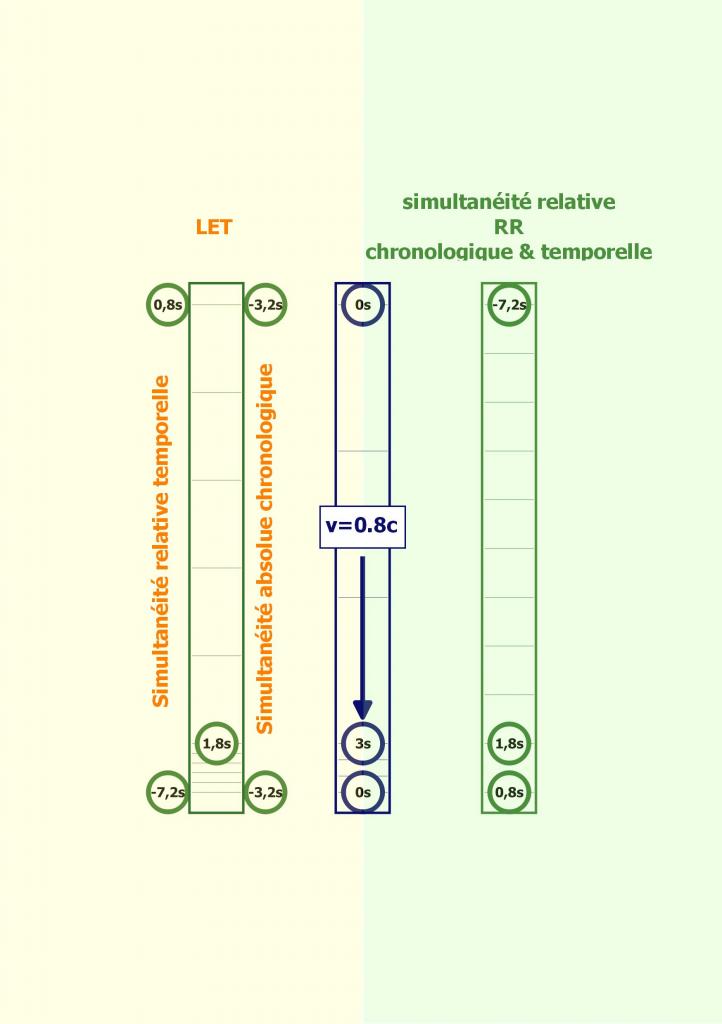
Là où cela devient intéressant est que si à t = 3s, O' croise O; O' verra l'avant et l'arrière du train coïncider avec les extrémités du quai et verra donc les horloges du quai afficher H=0s; mais les horloges du train afficheron respectivement 2s pour celle située à l'avant du train et -6s pour celle situé à l'arrière.
Comme t = Y * t' , t=3s -> t'=1,8s cela veut dire que à t=t'=0s , O' croise O, O' verra les horloges aux extrémités du quai afficher H= -3s et celles aux extrémités du train afficher 0,2s pour celle de l'avant du train et -7,8s pour celle de l'arrière du train.
D'où à mon avis la relativité de la simultanéité pour la LET.
Ce raisonnement vous paraît-il juste?
Cordialement,
Zefram
-----

[mach3]

Je ne comprends pas bien.

Il me semble que par principe, l’interprétation de Lorentz se base sur une simultanéité absolue (mais inconnaissable), celle donnée par des horloges synchronisées et immobiles par rapport à l'éther. Dans ce cadre tout observateur, quelque soit son mouvement, peut construire une simultanéité grâce des horloges immobiles par rapport à lui, mais cette simultanéité est "fausse" ou "illusoire", sauf si, par hasard, l'observateur est immobile par rapport à l'éther et dans ce cas il expérimente la "vraie" simultanéité, mais ça, personne ne peut le savoir.

Pour développer ce que je comprends de ça, Lorentz postule que comme en mécanique newtonnienne, l'espace-temps est stratifié de façon unique par un temps absolu, et qu'il y a donc un ordre absolu des évènements (comme en mécanique newtonnienne). Il postule aussi, comme en mécanique newtonnienne, que la lumière va à la vitesse c par rapport à l’éther. La mécanique newtonnienne prédit que l'on peut alors connaitre la vitesse d'un corps par rapport à l'éther justement par des mesures impliquant la lumière (Michelson et Morley), ce qui permet de connaitre le mouvement absolu, et donc le temps absolu (on doit pouvoir synchroniser les horloges sur le vrai temps absolu). Evidemment, cela est contre-dit par l'expérience, donc Lorentz postule qu'il y a "conspiration" des règles et des horloges qui fait que l'on ne peut pas mesurer la "vraie" vitesse de la lumière par rapport à nous et qu'on obtient systématiquement la même valeur "faussée" : l'éther de Lorentz contracte physiquement les objets dans le sens de leur déplacement par rapport à lui, et ralenti physiquement les horloges qui se déplacent par rapport à lui, exactement avec le même taux. Il est donc impossible en pratique de synchroniser les horloges sur le temps absolu. On peut synchroniser entre elles des horloges immobiles les unes par rapport aux autres néanmoins, elles tourneront simplement moins vite que le temps absolu, et ne paraitront synchrones que pour les observateurs immobiles par rapport à elles (par rapport à l'éther, aucune n'indique la même heure -sauf celles situées sur un même plan orthogonal à leur vecteur vitesse- et l'heure indiquée diminue si on va dans la même direction que les horloges), tout comme d'ailleurs des horloges marquant le temps absolu seraient ne paraitront synchrone que pour des observateurs immobile par rapport à l'ether. Ces horloges seront synchronisées du point de vue opérationnel pour les observateurs immobiles par rapport à elles, mais ils savent que ce n'est pas le temps absolu qu'ils lisent sur ces horloges et que la datation que cela donne aux évènements est faussée (c'est à dire que des évènements absolument simultanés pourront avoir des dates opérationnelles différentes et inversement).

C'est marrant ça me rappelle de vieilles discussions avec un "ami" commun

m@ch3

[JPL]

Quelle idée de ressortir cette vieillerie, même si ce fut une idée remarquable à son époque alors que la relativité d’Einstein a réponse à tous ces faux problèmes ?

[Mailou75]

Encore plus de la part de Zef, pour qui la RR est une «religion»

[A voir en vidéo sur Futura]

[Zefram Cochrane]

Bonjour à vous tous et merci pour vos réponses.

Encore plus de la part de Zef, pour qui la RR est une «religion»

Rassures-toi je n'ai pas changé de crêmerie et je ne suis pas prêt d'en changer.
https://fr.wikipedia.org/wiki/Tests_...ité_restreinte
Tu as trois test fondamentaux de la RR :
Michelson et Morlay
Kennedy et Thorndike
Ives et Stilwell
Si la LET est conforme avec MM et KT elle ne l'est pas avec IS.
En plus l'isotropie de la vitesse de la lumière est incontestablement prouvée expérimentalement grâce à l'effet Mössbauer qui démontre l'absence d'un vent d'éther sur un parcours one-way; ce qui invalide la LET.
https://fr.wikipedia.org/wiki/Expéri...;Ives-Stilwell
(expérience du disque tournant de Mössbauer)

Quelle idée de ressortir cette vieillerie, même si ce fut une idée remarquable à son époque alors que la relativité d’Einstein a réponse à tous ces faux problèmes ?

La LET et la RR présentent assez de similitudes pour permettre à notre ami (celui de mach3 et moi) d'affirmer que la LET est potentiellement aussi valide que la RR et que si on considère le principe philosophique de l'existence la relativité de la simultanéité aboutit à des absurdité, donc la LET est juste et qu'il existe une chronologie objective ( la chronologie du référentiel de l'éther) et donc un instant présent physique de l'univers.
Même si expérimentalement la LET est invalide ( ce qui laisse de marbre notre ami), il est rigolo et intéressant je trouve qu'on puisse mettre en évidence que la LET implique une relativité de la simultanéité au niveau physique et une simultanéité absolue illusoire du fait de la procédure mise en oeuvre pour synchroniser les horloges dans un référentiel en MRU par rapport à l'éther.
Par ailleurs comme me l'a fait remarquer récemment notre ami, la RR semble contredire un postulat d'existence chronologique parce que l'ordre temporel entre les événéments peut être inversé s'ils sont séparés par un intervalle d'espace-temps de genre espace.
C'est normal parce que lorsque deux événements sont séparés par un intervalle d'espace-temps de genre espace, l'ordre temporel est indéfini ce qui n'est pas le cas pour un instervalle d'espace-temps de genre temps ou de genre lumière.
Ainsi si A et B son séparés par un instervalle d'espace-temps de genre temps ou de genre lumière, B peut être causalement lié à A, donc A précède B. Ce qui veut dire que dans tous les cas de figure, un observateur externe verra A précéder B, et à la limite, les verra se produire simultanément.
Nous pouvons donc opposer au postulat d'existence basé sur la chronologie, un postulat d'existence basé sur la causalité.
Il est, à mon humble avis, intéressant de déterrer parfois de vieux trucs pour pouvoir les comparer.
Cordialement
Zefram.
P.S je ferrais une réponse détaillée à mach3 séparément.

[mach3]

Si la LET est conforme avec MM et KT elle ne l'est pas avec IS.
En plus l'isotropie de la vitesse de la lumière est incontestablement prouvée expérimentalement grâce à l'effet Mössbauer qui démontre l'absence d'un vent d'éther sur un parcours one-way; ce qui invalide la LET.
https://fr.wikipedia.org/wiki/Expéri...;Ives-Stilwell
(expérience du disque tournant de Mössbauer)

bizarre, il me semblait que la LET n'était qu'une interprétation de la RR et donc donnait les mêmes résultats expérimentaux. Pourquoi n'y aurait-il pas d'effet Doppler transverse en LET?

m@ch3

[Deedee81]

Salut,

bizarre, il me semblait que la LET n'était qu'une interprétation de la RR et donc donnait les mêmes résultats expérimentaux. Pourquoi n'y aurait-il pas d'effet Doppler transverse en LET?

Je connais assez mal la LET mais pour ce que j'en sais, pour moi aussi c'est juste interprétation/reformulation de la RR et donc les mêmes résultats.

Personnellement je me méfie fortement de ce genre d'interprétation car elle introduit des glissements de sens qui peuvent entrainer des confusions.
Un exemple que je connais mieux est la jauge de Selleri qui conduit à une vitesse de la lumière non invariante. Sauf que le mot "vitesse" est trompeur car ça ne correspond pas à la pratique de la mesure et diffère donc du mot "vitesse" utilisé habituellement en relativité. Dangereux.

Je ne sais pas si le problème ici est du même ordre.
EDIT Rappelons que l'effet Doppler transverse est totalement équivalent à la dilatation du temps. S'il y a dilatation du temps en LET alors il doit y avoir effet Doppler transverse.

[Zefram Cochrane]

bizarre, il me semblait que la LET n'était qu'une interprétation de la RR et donc donnait les mêmes résultats expérimentaux. Pourquoi n'y aurait-il pas d'effet Doppler transverse en LET?

m@ch3

Bonjour,
Mon raisonnement est le suivant:
La LET est incompatible avec l'expérience d'Ives et Stilwell parce que si on se place du point de vue d'un observateur stationnaire dans le référentiel de l'éther (Bleu):
du fait du MRU, Il voit Vert ( mobile en MRU à v=0,8c) blueschifté d'un facteur Yv =5/3 ( EDT), mais comme le temps s'écoule moins vite pour Vert que pour lui d'un facteur Yv, il voit Vert avec un EDT de 1, c'est-à-dire , ni blueschifté ni redschifté.
De son coté Vert voit, du fait du MRU, Bleu bueshifté d'un facteur Y et comme le temps s'écoule plus vite pour Bleu d'un facteur Yv il voit Bleu blueschifté d'un facteur Yv². Mais ça, il ne peut le savoir parce que si Rouge est en MRU à U par rapport à Bleu, Bleu voit Rouge avec un EDT de 1, donc Vert verra Rouge blueschifté d'un facteur Yv².
D'où l'incompatibilité, si mon raisonnement est juste, avec l'expérience d'Ives et Stilwell.

[Deedee81]

Holàlà C'est pas clair c'est bleu vert qui rougissent.

Il y a juste un truc qui me chiffonne :
"si on se place du point de vue d'un observateur stationnaire dans le référentiel de l'éther"

Mais pourquoi devrait-on uniquement considérer cet observateur ???

[Zefram Cochrane]

Bonjour Deedee.
dans la LET, la vitesse de la lumière est isotrope uniquement dans le référentiel de l'éther qui est un référentiel privilégié à partir duquel on calcule la contraction des longueurs et la diltation du temps ( la conspiration des règles et horloges mentionnés décrit par mach3 et 2 des postulats de mon premier message)
un point de détail où je ne suis pas d'accord avec mach3 est qu'en cinématique newtionienne il n'y a pas de référentiel d'éther par ce que la vitesse de la lumière est isotrope dans le référentiel de la source et anisotrope dans le référentiel de l'observateur ( y compris si celui-ci se trouve dans le référentiel de l'éther).
Historiquement, l'expérience de MM visait à vérifier que la vitesse de la lumière était anisotrope dans un référentiel différent de l'éther avec durées et longueurs absolues la "conspiration" est venue après.

[Deedee81]

Ca ne répond pas vraiment à ma question.
Et j'avais donné mon sentiment aussi sur le fait que LET doit avoir les mêmes prédictions expérimentales.

Mais je suis obligé de laisser d'autres approfondir le problème car je ne maîtrise pas assez la LET.

Concernant Newton, la question est plus compliquée qu'il n'y parait puisque :
- Newton considérait une lumière corpusculaire (et elle ne peut servir de référence pour un éventuel éther)
- La théorie respecte la relativité galiléenne
- Mais Newton considère un référentiel absolu (il distingue "grandeurs mathématiques" des "grandeurs vraies mais pas nécessairement mesurables")
Evitons de tomber dans les anachronismes

[Nicophil]

Bonjour,

référentiel privilégié à partir duquel on calcule la contraction des longueurs et la diltation du temps (la conspiration des règles et horloges)

référentiel privilégié dans lequel on mesure la contraction des règles et le ralentissement des horloges (la conspiration des règles et horloges en mouvement)

[Zefram Cochrane]

@mach3


J'ai fait un schéma pour montrer la différence entre la LET et la RR
Au centre se trouve Bleu au milieu d'un quai de 6s.l de longueur dans la perspective de Vert qui est commune à la LET et la RR.
à droite se trouve la perspective de Vert de la RR qui est connue et à gauche celle de Vert pour la LET.
Notez que dans le cadre de la RR, Vert ne se trouve pas au milieu du train tandis que dans le cadre de la LET si ( traits verts)
Dans la RR la relativité de la simultanéité est temporelle et physique, tandis que pour la LET elle est temporelle quand on considère les temps parcours des signaux lumineux du point de vue de Vert; mais la simultanéité devient absolue si on applique la procédure de synchronisation suivante.
à un instant T , Vert au centre du train (1.8s) envoie un signal lumineux vers les horloges situées à l'extrémités du train leur demandant d'afficher T+5s.
le signal envoyé vers l'avant du train met 9s à arriver à l'horloge et donc l'horloge affiche un retard de 4s, mais comme un signal ne met qu'une seconde à revenir , à T+10s Vert verra bien l'horloge de l'avant du train afficher T+5s.
Même raisonnement pour le signal envoyé à l'horloge de l'arrière du train qui ne met qu'une seconde à lui parvenir et qui dont l'horloge affiche 4s d'avance. Sur le retour, un signal met 9s. Donc à T+10s Vert voit bien l'horloge de l'arrière du train afficher T+5s.
On voit bien dans le cadre de la LET le coté artificiel de la synchronisation des horloges.
Etes-tu d'accord?
Cordialement,
Zefram
merci pour ta précision Nicophil

[mach3]

Je n'ai toujours pas décortiquer les posts, mais j'avais besoin au préalable, de comprendre comment marchait l'effet Doppler transverse en LET.

On considère un étherien, immobile par rapport à l'éther, et un terrien, mobile par rapport à l'éther. Au moment où la vitesse du terrien par rapport à l'éther est orthogonale à la ligne reliant les positions de l'étherien et du terrien, le terrien envoie un rayon lumineux. Dans cette configuration, il n'y a pas d'effet Doppler classique, car le récepteur est immobile tandis que l'émetteur ne s'éloigne ni ne s'approche du récepteur au moment où il émet (les et de la formule doppler classique sont nuls). Le terrien mesure la fréquence de son rayonnement quand il l'émet. Il trouve . Seulement, il ne s'en rend pas compte, mais ses horloges sont ralenties par leur mouvement dans l'éther. La fréquence absolue (mesurée avec le temps absolu) est .
L'étherien reçoit le rayonnement, de fréquence . Effet Doppler transverse, même prédiction qu'en RR.

Considérons maintenant que l'étherien envoie un rayon lumineux au terrien. Il peut l'envoyer de façon à ce que le rayon atteigne le terrien au moment où la vitesse du terrien par rapport à l'éther est orthogonale à la ligne reliant les positions de l'étherien et du terrien. Dans cette configuration, il n'y a pas d'effet Doppler classique, car l'émetteur est immobile et le récepteur ne s'éloigne ni ne s'approche de la cible au moment où il reçoit (les et de la formule doppler classique sont nuls). L'etherien envoie la fréquence f_e. Le terrien devrait recevoir un rayonnement de fréquence f_e. Seulement ses horloges sont ralenties par leur mouvement dans l'éther, donc il mesure un rayonnement de fréquence . WTF? du blueshift? transverse? prédiction inverse de la RR?

En fait non. Il y a une faille. On a oublié l'aberration de la lumière pour le terrien. Quand il reçoit le rayon de l'étherien, il voit l'etherien en train de se rapprocher de lui, il n'est pas encore passé au plus près, sa vitesse n'apparait pas encore transverse pour le terrien. Comme il voit l'etherien s'approcher de lui, il n'est pas étonnant que le terrien voit ses signaux blueshiftés. C'est même plutôt cohérent.
Il faut en fait que l'étherien attende un peu plus pour émettre. Il faut qu'il émette au moment où la vitesse du terrien par rapport à l'éther est orthogonale à la ligne reliant les positions de l'étherien et du terrien. Cela implique qu'il l'émette avec un angle par rapport à cette ligne, car il faut que le rayon atteigne le terrien qui avance (*). Au moment où le terrien reçoit le rayon, il s'éloigne (v_{rec} positive). Il reçoit donc un rayonnement affecté par l'effet Doppler classique, de fréquence moindre que f_e. Certes, son horloge tournant au ralenti, il mesurera une fréquence pas si ralentie que cela, mais elle devrait être ralentie quand même. Je ne l'ai pas encore démontré, mais j'anticipe que l'effet Doppler classique donnera une fréquence absolue de , et que le ralentissement de l'horloge du terrien l'amènera à mesurer la fréquence , l'effet Doppler transverse, comme prédit en RR.

En revenant à la RR normale, on voit bien aussi la faille. Si l'étherien se débrouille pour que son signal arrive au terrien quand celui-ci est au plus proche, c'est bien un signal blueshifté que le terrien reçoit. Il faut que l'étherien émette quand le terrien est au plus près pour qu'il n'y ait que du doppler transverse pur.

Bref, mis-à-part un petit point encore à démontrer proprement (mais qui ne fait aucun doute), la LET prédit correctement l'effet Doppler transverse, et il s'agit bien d'une interprétation différente de la RR, pas d'une théorie différente.

m@ch3

[mach3]

C'est bon c'est démontré. L'étherien est au point A. Au moment, où le signal est émis par l'étherien, le terrien est en B et au moment où le signal est reçu par le terrien, celui-ci est en C. Le triangle ABC est rectangle en B (la vitesse du terrien, colinéaire à BC, est orthogonale à la ligne joignant étherien et terrien à l'émission, qui est (AB)). Le coté AC mesure (parcouru par la lumière en une durée t), le coté BC mesure (parcouru par le terrien à la vitesse v en une durée t). Le sinus de l'angle CAB est donc . La vitesse du terrien se décompose en une composante radiale suivant AC, , celle qui compte pour l'effet Doppler classique et une composante orthoradiale, orthogonale à la radiale. On peut tracer la hauteur issue de B du triangle ABC et coupant AC en D pour matérialiser cette décomposition. DC étant de longueur et l'angle DBC étant égal à l'angle CAB, on a .
D'où .

Introduit dans le Doppler classique, cela donne une fréquence reçue absolue de :



Donc cela donne une fréquence mesurée par le récepteur (en utilisant donc le temps de ses horloges ralenties et non le temps absolu) :



Affaire classée concernant le doppler transverse. Ives et Stillwell n'invalide pas la LET. D'ailleurs Ives était partisan de la LET :

Subsequent to the advent of special relativity, only a small number of individuals have advocated the Lorentzian approach to physics. Many of these, such as Herbert E. Ives (who, along with G. R. Stilwell, performed the first experimental confirmation of time dilation) have been motivated by the belief that special relativity is logically inconsistent, and so some other conceptual framework is needed to reconcile the relativistic phenomena. For example, Ives wrote "The 'principle' of the constancy of the velocity of light is not merely 'ununderstandable', it is not supported by 'objective matters of fact'; it is untenable..."

Concernant le Moss-Bauer, quels arguments vont dans le sens d'une mesure one-way?

m@ch3

[Zefram Cochrane]

Bonjour, et merci beaucoup de tes réponse Mach3
Je prend comme formule de l’EDT*:
Fo = Fs / Y
https://fr.wikipedia.org/wiki/Effet_Doppler_relativiste

Cela correspond en RR à la fréquence de réception Fo par un observateur O qui voit une source S émettre un éclat lumineux à la fréquence Fs à l’instant où O voit la source S passer au plus près de lui ( la vitesse de la source par rapport à l’observateur est orthogonale à la ligne reliant la source et l’observateur).
Du fait du MRU, l’observateur verra la source redschifté d’un facteur de Lorentz lorsqu’il verra la source passer au plus près de lui*:
Fo = Fs / Yv
Soit un Ethérien et un Terrien en MRU à V chacun sont équipés d’un maser. Comme nous sommes dans le cadre de la LET, à cause de la dilatation du temps on pose*:
Fe = Yv * Fe’
Fe est la fréquence du maser de l’Ethérien et Fe’ est celle du Terrien mais comme le temps s’écoule Y fois moins vite sur Terre que dans l’éther du point de vue du Terrien, Fe’ = Fe en ce sens que la lumière émise par un maser qu’il soit sur Terre ou dans l’Ether sera perçu par le Terrien ( pour le maser terrestre ) ou l’Ethérien ( pour le maser de l’Ether) de la même manière.
Partant de là . L’Ethérien voit le Terrien passé au plus près de lui et donc du fait du MRU, l’Ethérien voit la lumière émise par le maser redschiftée d’un facteur de Lorentz comme en RR et en plus*: comme le temps s’écoule physiquement moins vite sur Terre que dans l’Ether d’un facteur de Lorentz. L’Ethérien voit le maser du terrien à une fréquence Fo = Fe / Yv²
De son côté, lorsque le Terrien voit l’Ethérien passer au plus près de lui, du fait du MRU, il voit le maser redschifté d’un facteur de Lorentz et en plus comme le temps s’écoule physiquement plus vite dans l’Ether que sur Terre, il voit la lumière émise par le maser de l’Ethérien blueschiftée d’un facteur de Lorentz. Le Terrien voit donc la lumière émis par le maser de l’Ethérien à une fréquence Fo’ = Fe’.

Ce n’est pas ce que tu décris, dans ton premier post voyons pourquoi.

On considère un étherien, immobile par rapport à l'éther, et un terrien, mobile par rapport à l'éther. Au moment où la vitesse du terrien par rapport à l'éther est orthogonale à la ligne reliant les positions de l'étherien et du terrien, le terrien envoie un rayon lumineux.
Dans cette configuration, il n'y a pas d'effet Doppler classique, car le récepteur est immobile tandis que l'émetteur ne s'éloigne ni ne s'approche du récepteur au moment où il émet (les et de la formule doppler classique sont nuls). Le terrien mesure la fréquence de son rayonnement quand il l'émet. Il trouve . Seulement, il ne s'en rend pas compte, mais ses horloges sont ralenties par leur mouvement dans l'éther. La fréquence absolue (mesurée avec le temps absolu) est .
L'étherien reçoit le rayonnement, de fréquence . Effet Doppler transverse, même prédiction qu'en RR.

D’après ce que je comprend*:
Pour moi, il faut considérer ce que nous enseigne l’expérience de la lanterne du mât du bateau*:
à T=T’=0s, le Terrien ( en Bleu) passe au plus près de l’ Ethérien (en Bleu), du point de vue du Terrien, la vitesse de l’Ethérien n’est par orthogonale à sa position apparente ( aberration de la lumière), il doit donc anticiper la position de l’Ethérien s’il veut que son tir de canon laser l’atteigne et doit donc tirer en oblique.
Lorsque l’Ethérien est atteint par le tir du Terrien, il est atteint verticalement (aberration de la lumière) et de son point de vue, la vitesse du Terrien est orthogonale à sa position apparente.
De fait, si le faisceau laser est émis à une fréquence Fe’, il y a un premier redschift d’un facteur de Lorentz qui s’opère.
Mais dans la LET, nous devons considérer également le fait que le temps s’écoule moins vite sur Terre que dans l’Ether*; il reçoit donc un faisceau lumineux avec une fréquence observé d’un facteur de Lorentz carré fois moindre que la fréquence d’émission.

Considérons maintenant que l'étherien envoie un rayon lumineux au terrien. Il peut l'envoyer de façon à ce que le rayon atteigne le terrien au moment où la vitesse du terrien par rapport à l'éther est orthogonale à la ligne reliant les positions de l'étherien et du terrien. Dans cette configuration, il n'y a pas d'effet Doppler classique, car l'émetteur est immobile et le récepteur ne s'éloigne ni ne s'approche de la cible au moment où il reçoit (les et de la formule doppler classique sont nuls). L'etherien envoie la fréquence f_e. Le terrien devrait recevoir un rayonnement de fréquence f_e. Seulement ses horloges sont ralenties par leur mouvement dans l'éther, donc il mesure un rayonnement de fréquence . WTF? du blueshift? transverse? prédiction inverse de la RR?

Si on inverse les rôle dans le cas de figure précédent. Du fait du MRU, la fréquence est redschiftée d’un facteur de Lorentz mais si on considère en plus que le temps s’écoule plus vite dans l’Ether que sur Terre d’un facteur de Lorentz, on trouve que le Terrien reçoit verticalement le tir de l’Ethérien ( aberration de la lumière) mais avec une fréquence à la réception identique que celle à l’émission.

En fait non. Il y a une faille. On a oublié l'aberration de la lumière pour le terrien. Quand il reçoit le rayon de l'étherien, il voit l'etherien en train de se rapprocher de lui, il n'est pas encore passé au plus près, sa vitesse n'apparait pas encore transverse pour le terrien. Comme il voit l'etherien s'approcher de lui, il n'est pas étonnant que le terrien voit ses signaux blueshiftés. C'est même plutôt cohérent.

Non je ne comprends pas trop, au moment où l’Ethérien ou le Terrien tirent, ils ne voient pas leur cible avec une vitesse orthogonale à leur position apparente du fait de l’aberration de la lumière comme tu le décris.
Si on tient compte du fait que dans la LET, le temps s’écoule moins vite sur Terre que dans l’Ether, au moment du tir*:
Le Terrien voit les signaux de l’Ethérien avec une fréquence observée blueschiftée d’un facteur de Lorentz carré fois plus que leur fréquence d’émission.
L’Ethérien voit les signaux du Terrien avec une fréquence observée égale à leur fréquence d’émission.
Je ne vois pas où se trouve l’erreur dans mon raisonnement, mais si tu en vois une, merci de me l’indiquer parce que c’est un sujet sur lequel je potasse depuis de longs mois*; je peux me tromper , c’est déjà arrivé à d’autres…

[mach3]

J'ai beaucoup de difficultés à te suivre... Et plutôt que d'essayer de décrypter, je vais aller plus profondément dans l'analyse.

Plaçons nous exclusivement dans le repère de l'éther. L'Etherien E est immobile. Le terrien T est mobile avec une vitesse c/2 et passe au plus près à une distance . Disons que l'Etherien est au point A et que le Terrien parcours la droite (D) dont le point B est tel que AB orthogonal à (D). Plaçons aussi les points C et C', qui seront sur la droite (D), à 1/2 de B tels que le Terrien croisera dans l'ordre C, B puis C'. L'Etherien est muni de trois "tubes" pour capter les signaux, orientés vers la droite (D), l'un suivant AB, et les deux autres faisant un angle de 30° avec AB, suivant AC et AC'. Le Terrien est lui aussi muni de tels tubes, orienté dans le sens inverse (vers la droite parallèle à (D) qui porte le point A) et vu du repère de l'éther, l'un est parallèle à BA et les deux autres font un angle de 30° avec BA, suivant CA et C'A (on se moque pour l'instant des orientations perçues par le Terrien pour ces tubes). On imposer que pour émettre ou capter un signal avec succès, celui-ci doit impérativement passer dans les tubes.

Admettons que le Terrien émette, pour que la communication se fasse avec succès, il y a deux options :
T1) Le Terrien émet depuis le point C (quand il est à une distance 1/2 avant le point B) par le tube parallèle à AB, le signal arrive donc à l'Etherien via son tube parallèle à AC
T2) Le Terrien émet depuis le point B, par le tube parallèle à C'A, le signal arrive donc à l'Etherien via son tube parallèle à AB

Admettons que l'Etherien émette, pour que la communication se fasse avec succès, il y a deux options :
E1) L'Etherien émet quand le Terrien est au point C, par le tube parallèle à AB, le signal arrive au Terrien via son tube parallèle à CA
E2) L'Etherien émet quand le Terrien est au point B, par le tube parallèle à AC', le signal arrive au Terrien via son tube parrallèle à AB

J'ai représenté ces situations sur le schéma joint.



Ces situations étant posées, nous allons les analyser dans le prochain message.

m@ch3

[mach3]

(note : pas lu le message précédent)

Reprenons, toujours dans le référentiel de l'éther. On ne parlera pour l'instant que de fréquences absolues, c'est à dire mesurées par des horloges donnant le temps absolu.

Commençons par regarder les vitesses de l'émetteur et du récepteur au sens de la convention ci-après pour ces différentes situations.

les vitesses seront comptées comme positives suivant la direction et dans le sens de propagation du signal (de l’émetteur vers le récepteur). Ainsi une vitesse positive et négative correspondra à un rapprochement entre source et récepteur tandis qu’une vitesse négative et positive correspondra à un éloignement.

T1 : ,
T2 : ,
E1 : ,
E2 : ,

Calculons les effets Doppler classiques correspondants suivant la formule :



T1 : : blueshift, le Terrien se rapproche de l'Etherien quand il émet
T2 :
E1 :
E2 : : redshift, le Terrien s'éloigne de l'Etherien quand il reçoit

Introduisons maintenant les fréquences relatives au Terrien. Le Terrien, en mouvement par rapport à l'éther à c/2, mesure les fréquences avec ses propres horloges qui n'indiquent pas le temps absolu mais un temps ralenti d'un facteur

Le Terrien considère, d'après ses horloges ralenties, des fréquences , qui correspondent à des fréquences absolues . Notons que les relations précédentes sont toujours correcte si on remplace et par et (simplement multiplication à droite et à gauche par )

Donc, l'effet Doppler tenant compte du ralentissement des horloges est :

T1 : : toujours du blueshift, quoique un peu atténué.
T2 : : Doppler transversal
E1 : : même blueshift que pour la situation T1 mais en inversant émetteur et récepteur
E2 : : même redshift que pour la situation T2 mais en inversant émetteur et récepteur --> c'est la même valeur que le Doppler transversal.

Histoire d'éclaircir encore plus les choses, je vais refaire un bilan en considérant une vitesse par rapport à l'éther quelconque du Terrien dans un prochain post.

m@ch3

[Zefram Cochrane]

Pas encore très au clair moi-même...


Mieux comme-cà:
ABC trois balise du référentiel de l'éther.
lorsque le Terrien arrive en B il tire en anticipant la position de l'Ethérien comme indiqué sur le schéma. De son point de vue l'orientation des canons n'est pas colinéaire.
Lorsque l'Ethérien reçoit le tir, il voit le Terrien arriver en B ; il voit les canons orientés colinéairement. S'il veut ripister il devra viser le point C pour atteindre le Terrien.
cela correspond plus aux cas de figure évoqués dans tes croquis.
Edit mach3 perds pas ton temps annule le message précédent STP

[mach3]

Pas d'avis sur ce que voit le Terrien pour l'instant. Je ne veux pas "m'inflencer" en suivant des raccourcis, un de mes objectifs étant de reconstruire le point de vue du Terrien en partant de prémisses simples.

Pas l'impression qu'on soit d'accord sur le schéma de droite. Où alors je ne le comprends pas.

Point de réflexion pour s'occuper l'esprit ce week-end : si on place un miroir parallèle à (D) entre l'etherien et le terrien, dans quelles conditions (émission et réception par quel tuyau) le Terrien peut il recevoir la réflexion du signal qu'il a émis lui même ?

m@ch3

[Zefram Cochrane]

Re arghhh! DSL Mach

Le Terrien se déplace dans l'Ether de A vers C à 0.8c.
lorsque l'Ethérien voit le Terrien en A, le Terrien se trouve déjà en B donc si l'Ethérien veut l'atteindre d'un tir de canon laser, il devra anticiper la position du Terrien et devra viser C.
Lorsque le Terrien est atteint par le tir de l'Ethérien, du fait de l'aberration de la lumière, le Terrien voit l'Ethérien perpendiculairement par rapport à l'axe de la trajectoire.
Normalement, et c'est à confirmer, on peut inverser les rôles de l'Ethérien et du Terrien SVP

A partir de là, notre interprétation diverge.
Ce que je dis est que dans le cadre de la RR, il n'y a pas de dilatation physique du temps, tandis que dans la LET si ( si on doit mettre 500s dans l'Ether pour cuire un oeuf , il faudra sur Terre en MRU à 0.8c par rapport à l'Ether 300s ).
Donc dans le cadre de la RR, un tir de laser émis par l'Ethérien avec une fréquence serait perçu par le Terrien avec une fréquence .
Mais, comme il nous faut également tenir compte du fait que le temps s'écoule moins vite sur Terre que dans l'Ether d'un facteur gamma.
Donc la fréquence observée par le Terrien sera
Dans l'hypothèse où l'on peut inverser les rôles :
on aura à la réception par l'Ethérien d'un tir du Terrien la relation entre les fréquences :
Je ne comprends pas pourquoi notre interprétation diverge et où se situe mon erreur?

[Archi3]

je ne cherche même pas à comprendre votre discussion, mais comment est ce qu'il pourrait y avoir une différence entre les observables dans la théorie de Lorentz et la théorie d'Einstein, si les formules de transformation de référentiel sont les mêmes ?

[Archi3]

Mais, comme il nous faut également tenir compte du fait que le temps s'écoule moins vite sur Terre que dans l'Ether d'un facteur gamma.

Ça c'est faux de dire ça comme ça. Ce n'est vrai que pour des couples d'évènements situés au même endroit sur la Terre, mais pas entre des évènements ayant lieu à des endroits différents, puisque le décalage temporel dépend du lieu.

[mach3]

je ne cherche même pas à comprendre votre discussion, mais comment est ce qu'il pourrait y avoir une différence entre les observables dans la théorie de Lorentz et la théorie d'Einstein, si les formules de transformation de référentiel sont les mêmes ?

Pour moi il est évident qu'il n'y a pas de différence entre les observables. Par contre il semble que ça ne le soit pas pour Zefram.

m@ch3

[Archi3]

donc a priori si Zefram fait une erreur de raisonnement, il ferait la même dans la théorie de la relativité "orthodoxe" . La plupart du temps, l'erreur commise est la même, et revient à penser que dans un référentiel, le temps "ralentit" globalement par rapport à un autre, c'est à dire que tout intervalle de temps mesuré dans un référentiel doit être multiplié par gamma dans un autre. Alors que ce n'est vrai que pour les durées entre deux évènements ayant lieu au même endroit dans le premier référentiel.(condition qu'on oublie de vérifier quand on fait l'erreur !!)

[mach3]

Zef, ce que tu décris avec le schéma correspond à la situation E2. Dans cette situation, la vitesse par rapport à l'ether du Terrien lors la réception n'est pas uniquement transverse, il faut donc calculer un effet Doppler classique. La fréquence absolue émise fem devient une fréquence absolue recue fem(1-vrec/c) avec vrec la vitesse du Terrien projetée sur le rayon lumineux. On est pour l'instant purement classique, on applique le Doppler classique, l'ether étant le milieu de propagation et les vitesses étant exprimées par rapport à lui et projetées sur le rayon lumineux.
Après on converti la fréquence absolue en fréquence relative au Terrien en tenant compte du rythme des horloges Terriennes ralenti par leur mouvement dans l'ether. On retrouve alors le même changement de fréquence que pour le Doppler transverse relativiste.

m@ch3

[Nicophil]

Hé hé, vous êtes partis sur le cas précis où il y a** une différence "physique" entre Poincaré et Einstein, discutée ici par Pierseaux, page 14/54 : http://cds.cern.ch/record/921614/files/0601090.pdf


** ou plutôt il y aurait, car c'est inmesurable en pratique...

[Zefram Cochrane]

Bonjour à tous et merci de votre participation à ce sujet.
Je peux avoir tout faux avec la mécanique classique et la LET et tout bon avec la RR parce que je ne me suis pas familiarisé avec l'aberration de la lumière et l'effet Doppler dans le cadre de la mécanique classique contrairement à la RR où j'ai une méthode fastoche pour la RR.

donc a priori si Zefram fait une erreur de raisonnement, il ferait la même dans la théorie de la relativité "orthodoxe" . La plupart du temps, l'erreur commise est la même, et revient à penser que dans un référentiel, le temps "ralentit" globalement par rapport à un autre, c'est à dire que tout intervalle de temps mesuré dans un référentiel doit être multiplié par gamma dans un autre. Alors que ce n'est vrai que pour les durées entre deux évènements ayant lieu au même endroit dans le premier référentiel.(condition qu'on oublie de vérifier quand on fait l'erreur !!)

Les TLs donnent les coordonnées ET d'un événement dans le référentiel K' connaissant celle de K ( on suppose les horloges de K et de K’ synchronisées)
On pose et
Les TLs:




Soit O’ en MRU à v=0,8c le long d’une voie de 48s.l de longueur propre*; soit une voie parallèle de 48s.l de longueur propre située à 36s.l de distance. Si lorsque O arrive au milieu de la voie , l’horloge du milieu de la voie indique T=0s, alors toute autre horloge située à distance S afficherait – T.
Nous aurions donc:




Si l’horloge distante de O’ affiche -T’, cela veut dire qu’elle se trouve une distance S’ de O’.




En faisant le rapport S'/S j’obtiens l’effet Doppler et les autres coordonnées mettent en évidence l’aberration relativiste de la lumière.

Si on regarde le schéma on voit que O' voit l’horloge du milieu de la voie battre à l’instant où il la croise gamma fois plus vite que la sienne, mais cette dilatation du temps n’est pas plus physique que les vitesses de battements des autres horloges qu’il voit à cet instant.
Il faut que je fasse une sérieuse MAJ pour la mécanique classique et la LET pour l’effet Doppler et l’aberration de la lumière; mais si pour ce qui est de l'aberration de la lumière on a la même chose en LET qu'en RR, vu qu'il y a dilatation physique du temps dans le référentiel K' par rapport à K de l'Ether, je multiplierais toutes les valeurs par gamma pour deux trains de 48s.l en MRU à v=0.8c avec O' l'observateur de l'Ether et je diviserais ces valeurs par gamma pour O' en MRU à v=0.8c par rapport à deux voies dans l'Ether.
Maintenant, comme je le disais, j'ai besoin d'une MAJ sur ces questions.
Cordialement,
Zefram

[Zefram Cochrane]

Bonjour,
Je m'essaye au calcul Doppler classique.
Avec Newton, la vitesse de la lumière est constante dans le référentiel de la source et anisotrope dans celle du récepteur.
Donc si la source se déplace dans le sens positif des x en MRU à V, si elle tire un fasceau laser depuis une coordonnée X verticalement verticalement vers le sens négatif des y , elle atteindra l'observateur situé aux coordonnées (X= 0 ; Y =0) au bout d'une durée T=Y/c et la vitesse de la lumière d'approche du faisceau sera :

La distance parcourue par le photon dans le référentiel de la source est :

Comme
On en déduit que
Pour moi, l'observateur verra la source émettre le faisceau verticalement (aberration de la lumière) avec un EDT :
That's sounds good for you?

[mach3]

Je m'essaye au calcul Doppler classique.
Avec Newton, la vitesse de la lumière est constante dans le référentiel de la source et anisotrope dans celle du récepteur.

Attention, la vitesse de la lumière est constante et isotrope dans le référentiel de la source si celle-ci est immobile par rapport au milieu de propagation. En fait peu importe les vitesses de la source ou du récepteur, c'est dans le référentiel du milieu de propagation qu'il y a isotropie. Et ce sont les composantes longitudinales des vitesses de la source et du récepteur (i.e. projetées sur le vecteur vitesse du signal) par rapport au milieu de propagation qui comptent pour l'effet Doppler.

Je n'ai pas décortiqué le calcul encore.

m@ch3