Bonjour,
Dans le cadre d'une discussion MP avec Franck84 ( P2B pour les intimes), je me suis interessé à la théorie de l'Ether de Lorentz (- Poincaré).
https://fr.wikipedia.org/wiki/Th%C3%...her_de_Lorentz
Selon eu, il existe un référentiel privilégié ce lui de l'Ether dans lequel la vitesse de la lumière se propage à c. Et, pour expliquer l'absence d'anisotropie dans la mesure de la vitesse de la lumière Lorentz à établi qu'une règle de longueur l dans l'ether devait se contracter dans le référentiel en mouvement et avoir une longueur l' telle que :
avec
.
De son coté, Poincaré disait que le temps devait se contracter par rapport au temps vrai t du référentiel de l'éther tel que
J'ai essayé de retrouver ces résultats.
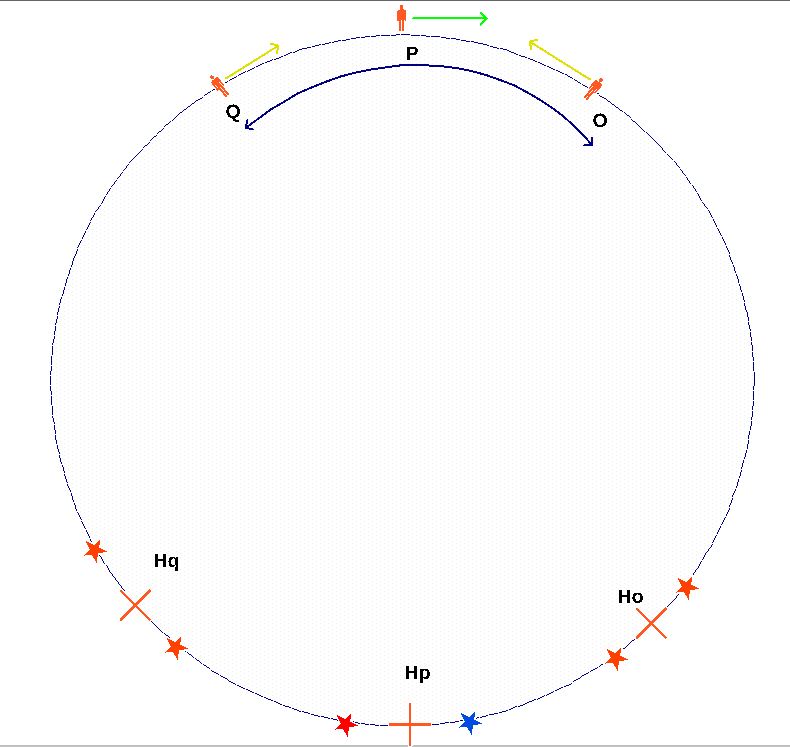
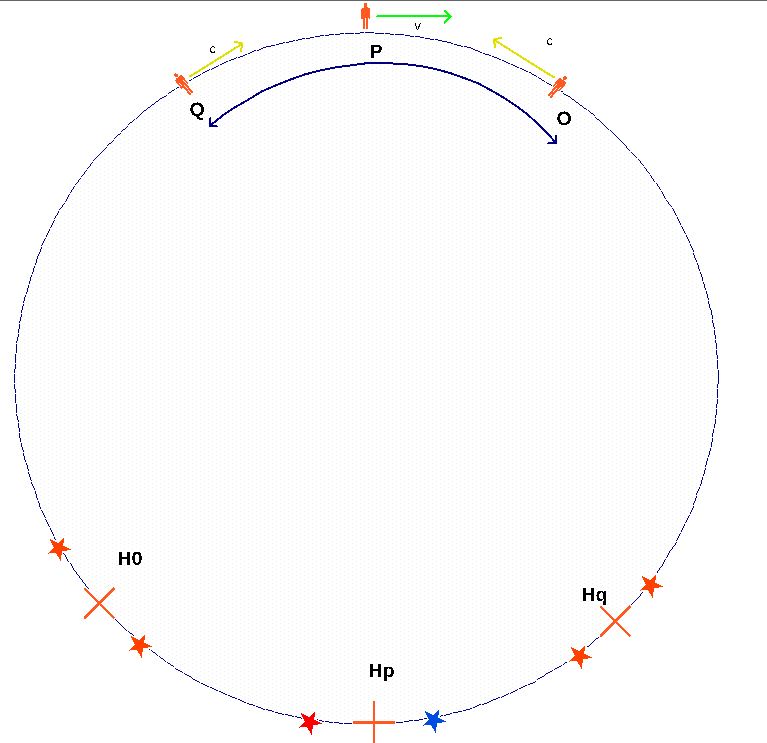
Soit le référentiel de l'Ether K et K' le référentiel en MRU à v par rapport à K.
À T = T'= 0s Q' et O' de K' sont séparé d'une longeur coordonnée L' dans K' et de L dans K. Soit P un observateur au repos situé au milieu de Q' et O' à T=T'=0s.
O' s'éloigne de P à v et Q' s'approche de P à v.
Suivant le principe de l'Ether luminifère de Lorentz. Si Q' et O' émettent à T=T'=0s un éclat lumineux l'un vers l'autre, le faisceau émis par O' s'approche de Q' à la vitesse c+v et et celui émis par Q' s'approche de O' à la vitesse c-v.
De leur point de vue, Q' et O' ne sauront pas à quelles dates dans le référentiel de l'Ether ils percevront les signaux émis par l'autre . Commes ils sont stationnaires et que leurs horloges sont synchronisées, ils se verront l'un l'autre avec un décallage temporel T' et diront qu'ils sont séparés de.
Soit T = L/c ce qui donneet
et donc

On a To = k*T' et Tq = h*T' . Pour le coups: abracadabra , k*h=1 (J'aimerais bien savoir comment Lorentz a fait pour la contraction des longueurs)
par conséquent :
Doncet
Question :
Si Q' et O' sont orange lorsqu'ils sont au repos dans le référentiel de l'Ether.
Q' ne devrait il pas voir O' de couleur orange bluschiftéeet O' ne devrait il pas voir Q' de couleur orange redschiftée
?
-----