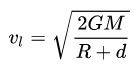Bonjour à toutes et à tous

Voilà les données du problème.
Dans le cas d’un astéroïde qui aurait initialement une vitesse relative nulle ou négligeable par rapport à sa cible la vitesse d’impact est au minimum égale à la vitesse de libération du corps impacté (à laquelle il faut ajouter la vitesse relative initiale s’il en a une).

Cette vitesse est donnée par la relation :
Nom : Vitesse de libération.jpg Affichages : 70 Taille : 6,0 Ko
  • G est la constante gravitationnelle ;
  • M est la masse de l'astre, en kilogrammes ;
  • R est le rayon de l'astre, en mètres ;
  • d est la distance de l'objet à la surface de l'astre, en mètres.

On considère ici que la masse de l’impacteur est négligeable par rapport à celle de l’impacté. Mais qu’en est-il dans le cas de Theia par exemple d’une masse par hypothèse comparable à celle de Mars donc non négligeable ? D’après mes calculs, la masse de Gaia, la proto-terre, devait être d’environ 90 % de celle de la Terre. La somme de leurs masses est égale à celle des masses de la Terre et de la Lune. Que devient l’équation ?
Étant donné que l’hypothèse la plus plausible est que Theia est née ou en tout cas se trouvait en orbite en L4 ou L5 avant de dériver vers la Terre on peut considérer que sa vitesse relative initiale était nulle et donc que seule l'accélération gravitationnelle les attiré l'une vers l'autre.
Mais je lis dans l’article de wiki en anglais Theia :
Computer simulations suggest that Theia was traveling no faster than 4 km/s (8,900 mph) when it struck Earth at an estimated 45 degree angle.
Cette vitesse me semble très faible. Comment la calcule-t-on ?

Merci d'avance de vos lumières.
Nico