
- Forum
- Futura-Sciences : les forums de la science
- UNIVERS
- Astronomie et Astrophysique
- Discussions libres
- Jamais rien ne tomba dans un trou noir ?
Jamais rien ne tomba dans un trou noir ?
- 16/08/2021, 08h52 #61mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
------
Never feed the troll after midnight!
- 23/08/2021, 23h56 #62Mailou75
- Date d'inscription
- novembre 2010
- Messages
- 5 602
Re : Jamais rien ne tomba dans un trou noir ?
Salut mach3,
Désolé j'ai mis loonngtemps à répondre, j'attendais d'avoir un ordi parce que les citations sur tablette ça soûle
Bon au final pas tant de citations que ça, mon excuse tombe à l'eau...
Ok, je crois comprendre. Le contenu de l'espace temps est étiré, surtout sur l'intervalle R=[0;4Rs]. Il vient remplir le trou noir en somme.Je reprécise que R est le rayon aréal qu'on note r habituellement et que r est "autre chose". En passant de R (le rayon aréal, variable radiale "habituelle") à r, ça va jouer significativement sur environ 3-4 fois rs, en effet, R et r sont égaux à moins d'un demi pourcent près pour R=4rs ou plus. La partie allant de R=rs à R~4rs va se retrouver dilatée suivant l'axe horizontal pour couvrir l'intervalle r=0 à r~4rs. Tu peux jeter un oeil à ce graphe desmos : https://www.desmos.com/calculator/l4uhtwsxhu
Ce que je comprends c'est que si je représente des trajectoires connues, j'obtiendrais une carte de ce qui se passe à l'extérieur (région I) donnant l'impression qu'il n'y a pas d’intérieur."chaque système de coordonnées a sa propre "métrique""... plus proprement il faut dire qu'il y a une expression différente de la même métrique pour chaque système de coordonnées. Mais là en l’occurrence, c'est deux fois la même expression, dans le même système de coordonnées.
Mais ce que je ne comprends pas, dans le débat, c'est que si on ajoute une dimension spatiale pour avoir de la 2D+t alors la surface du trou noir (4.Pi.Rs²) devient un point, en r=0 soit R=Rs. Les orbitales au dessus de Rs auront une circonférence bien plus courte que celle définie par le rayon aréal (2.Pi.R). Il y a donc une différence physique entre les deux modèles : l'un est à symétrie centrale, l'autre non. L'un est juste l'autre faux.
Ou alors je ne saisis pas où se trouve le débat. La version de Schw utilisant r est simplement un autre système de coordonnées 1D+t*, ni plus juste ni plus faux qu'un autre.
Quelqu'un pourrait-il résumer la question svp ?
*(auxquelles d'autres sont aussi contraints : Penrose, Kruskal... qui ne tournent pas autour d'un axe pour définir une dimension supplémentaire, respectant le rayon aréal R).
Mwai, accepter qu'une partie du modèle soit juste mais pas l'autre c'est pas très intègre... dans ce cas ça veut dire que l'on ne retient du modèle de Schw que l'effondrement (Oppenheimer ?) en coordonnées de Penrose ? Je pense que tu vois le graphe auquel je fais allusion...
A ce propos, les trous noir primordiaux sont ils des fruits d'effondrement ou du type "éternel" ?
Merci a +Dernière modification par Mailou75 ; 23/08/2021 à 23h57.
Trollus vulgaris
- 24/08/2021, 10h38 #63mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
Attention aux confusions carte/territoire. Ce n'est pas le contenu qui est étiré, mais la représentation. Quand le rayon aréal est utilisé comme coordonnée radiale, cela donne aux représentations des sphères "centrées sur l'origine" une fidèlité en terme de surface (la surface des sphères physiques est proportionnelle, voire égale, à la surface des représentations de ces sphères). Si on change de coordonnées radiale (comme ici, passer de R, rayon aréal, à r, qui ressemble au rayon aréal pour r grand mais tend vers 0 quand R tend vers rs), la fidelité est perdue. En effet en passant de R à r, une sphère de rayon aréal arbitrairement proche de rs aura une surface (physique, qui serait mesurable par un arpenteur) arbitrairement proche de , mais sera représenté par une sphère de surface arbitrairement petite. Bien comprendre : quelque soit le système de coordonnée, la sphère considérée possède la même surface, mais sa représentation varie. Exemple en cartographie : en projection de Mercator, le Groenland apparait comme étant quasiment aussi grand que le continent africain, mais le Groenland est toujours physiquement plus petit que le continent africain et ce n'est pas parce qu'on a choisi une carte de Mercator que sa taille va changer.
, mais sera représenté par une sphère de surface arbitrairement petite. Bien comprendre : quelque soit le système de coordonnée, la sphère considérée possède la même surface, mais sa représentation varie. Exemple en cartographie : en projection de Mercator, le Groenland apparait comme étant quasiment aussi grand que le continent africain, mais le Groenland est toujours physiquement plus petit que le continent africain et ce n'est pas parce qu'on a choisi une carte de Mercator que sa taille va changer.
Oui. Si on se limite à une image de la carte et qu'on a pas d'autres infos (pas d'échelle, pas d'indicatrice), alors on a l'impression qu'il ne manque rien sauf le point central. C'est comparable au fait d'avoir l'impression que la Terre est plate est qu'elle est bordée par l'antartique sur son pourtour quand on regarde une projection equidistante azimuthale de la surface du globe centrée sur le pole nord ( https://en.wikipedia.org/wiki/Azimut...jection_SW.jpg )
comme dit plus haut, ce n'est pas la surface du trou noir qui devient un point, mais sa représentation. La surface du trou noir ne dépend pas du système de coordonnées (comme toute chose qui peut se mesurer physiquement).
Idem, les représentations des orbites auront une circonférence bien plus courte, mais la circonférence (physique, mesurable par arpentage) des orbites ne change pas.
Pour appuyer dessus encore plus formellement, mathématiquement la circonférence s'obtient en intégrant l'intervalle le long du cercle, et cet intervalle s'obtient à partir de l'expression de la métrique. Quand on change de coordonnées, l'expression de la métrique change de façon à ce que la circonférence obtenue ne change pas.
Le théorème de Birkhoff dit que la solution de Schwarzschild s'applique dans toute région vide d'un espace-temps de symétrie sphérique (le paramètre rs de la solution devant être ajusté pour se recoller avec l'éventuelle région non vide interne à cette région vide). C'est des maths, donc il n'y a pas à se poser de questions d'intégrité.
m@ch3Never feed the troll after midnight!
- 24/08/2021, 11h58 #64mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
On peut aller encore plus loin en considérant par exemple la coordonnée de la tortue comme coordonnée radiale : https://en.wikipedia.org/wiki/Edding...ise_coordinate , rs se trouvera alors repoussé à l'infini négatifAttention aux confusions carte/territoire. Ce n'est pas le contenu qui est étiré, mais la représentation. Quand le rayon aréal est utilisé comme coordonnée radiale, cela donne aux représentations des sphères "centrées sur l'origine" une fidèlité en terme de surface (la surface des sphères physiques est proportionnelle, voire égale, à la surface des représentations de ces sphères). Si on change de coordonnées radiale (comme ici, passer de R, rayon aréal, à r, qui ressemble au rayon aréal pour r grand mais tend vers 0 quand R tend vers rs), la fidelité est perdue. En effet en passant de R à r, une sphère de rayon aréal arbitrairement proche de rs aura une surface (physique, qui serait mesurable par un arpenteur) arbitrairement proche de , mais sera représenté par une sphère de surface arbitrairement petite. Bien comprendre : quelque soit le système de coordonnée, la sphère considérée possède la même surface, mais sa représentation varie. Exemple en cartographie : en projection de Mercator, le Groenland apparait comme étant quasiment aussi grand que le continent africain, mais le Groenland est toujours physiquement plus petit que le continent africain et ce n'est pas parce qu'on a choisi une carte de Mercator que sa taille va changer.
, mais sera représenté par une sphère de surface arbitrairement petite. Bien comprendre : quelque soit le système de coordonnée, la sphère considérée possède la même surface, mais sa représentation varie. Exemple en cartographie : en projection de Mercator, le Groenland apparait comme étant quasiment aussi grand que le continent africain, mais le Groenland est toujours physiquement plus petit que le continent africain et ce n'est pas parce qu'on a choisi une carte de Mercator que sa taille va changer. et ça ne signifiera pas pour autant que le trou noir est de taille négative et infinie.
et ça ne signifiera pas pour autant que le trou noir est de taille négative et infinie.
m@ch3Never feed the troll after midnight!
- 25/08/2021, 00h25 #65Mailou75
- Date d'inscription
- novembre 2010
- Messages
- 5 602
Re : Jamais rien ne tomba dans un trou noir ?
Salut, merci

Oui oui, à partir du moment où tu as établi que les formules étaient équivalentes (ce sur quoi je te fais confiance), je ne parle que de systèmes de coordonnées, R (aréal) ou r (?).
Ok, peu d’intérêt à ajouter une dimension par rotation donc, puisque tout sera faussé. Autant dire que c'est un système 1D+t max.(...) En effet en passant de R à r, une sphère de rayon aréal arbitrairement proche de rs aura une surface (physique, qui serait mesurable par un arpenteur) arbitrairement proche de , mais sera représenté par une sphère de surface arbitrairement petite.
, mais sera représenté par une sphère de surface arbitrairement petite.
Oui une carte limitée. Si on suppose que la solution de Schw reste vraie alors c'est juste que le TN n'est pas représenté, ça ne veut pas dire qu'il n'existe pas. Donc par exemple ton "cet intervalle s'obtient à partir de l'expression de la métrique" pourrait être un argument pour Bernarddo démontrant que le r n'est pas une solution physique sans TN puisque la métrique, équivalente, donnerait, pour une représentation quasi ponctuelle, une grande surface aréale réelle. Isn't it ?Oui. Si on se limite à une image de la carte et qu'on a pas d'autres infos (pas d'échelle, pas d'indicatrice), alors on a l'impression qu'il ne manque rien sauf le point central. (...) Idem, les représentations des orbites auront une circonférence bien plus courte, mais la circonférence (physique, mesurable par arpentage) des orbites ne change pas.
Si je comprends bien, que la solution de Schw (courbure négative) est vraie à l'extérieur pour des astres de rayon > Rs. Ça ne prouve pas que les trous noirs existent ! lolLe théorème de Birkhoff dit que la solution de Schwarzschild s'applique dans toute région vide d'un espace-temps de symétrie sphérique (le paramètre rs de la solution devant être ajusté pour se recoller avec l'éventuelle région non vide interne à cette région vide). C'est des maths, donc il n'y a pas à se poser de questions d'intégrité.
Le curseur pointant la limite de la théorie est assez subjectif : Extérieur > Intérieur (courbure positive) > Trous noirs > Trous blancs > région III ...?
J'avais déjà entendu parler mais pas regardé de près. C'est amusant quand on regarde la définition du temps t' de Finkelstein, c'est exactement la même (à c près) que la définition de l'espace en coordonnées de la Tortue. De la même façon qu'une géodésique nulle entrante est une diagonale à 45° en coordonnées de Finkelstein (r;t') alors j'intuite qu'une représentation en coordonnées de la Tortue (r*;t) où t reste celui de Schw donnera aussi une diagonale à 45° pour une géodésique lumière entrante. Si je retrouve un jour du courage, j’ l’essayerai peut êtreOn peut aller encore plus loin en considérant par exemple la coordonnée de la tortue comme coordonnée radiale : https://en.wikipedia.org/wiki/Edding...ise_coordinate , rs se trouvera alors repoussé à l'infini négatif et ça ne signifiera pas pour autant que le trou noir est de taille négative et infinie.
et ça ne signifiera pas pour autant que le trou noir est de taille négative et infinie.

Merci a+Dernière modification par Mailou75 ; 25/08/2021 à 00h27.
Trollus vulgaris
- 25/08/2021, 14h27 #66mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
comme déjà dit plus haut, ce sont des arguments sur la métrique à l'intérieur de l'astre (partie non vide) qui permettent de penser qu'une région II peut apparaitre. Imaginons un astre dont le rayon est supérieur à son rayon de Schwarzschild. La métrique à l'extérieur est celle de Schwarzschild et la métrique à l'intérieur est spécifique à l'astre. C'est le contenu de l'astre qui va fixer cette métrique interne. Sauf cas particulier (par exemple sphère de poussière --> Lemaitre-Tolman-Bondi, ou sphère homogène et isotrope --> Friedmann-Lemaitre-Robertson-Walker), il n'y a pas de solution analytique, mais on peut inférer pas mal de choses en toute généralité.Si je comprends bien, que la solution de Schw (courbure négative) est vraie à l'extérieur pour des astres de rayon > Rs. Ça ne prouve pas que les trous noirs existent ! lol
Le curseur pointant la limite de la théorie est assez subjectif : Extérieur > Intérieur (courbure positive) > Trous noirs > Trous blancs > région III ...?
Par exemple, pour que l'astre possède un rayon statique, il faut que les particules situées à sa surface possèdent une accélération propre centrifuge (comme un immobile de Schwarzschild, car les géodésiques qui culminent au rayon arrivent de et repartent vers le centre de l'astre), donc qu'elles subissent une force, due à la pression interne de l'astre. Si la pression dans l'astre est plus élevée que requis, l'astre grandi, et inversement si la pression est moins élevée que requis, l'astre se contracte. Cela varie en fonction de la nature de la matière constituant l'astre, de son équation d'état, mais en général une expansion se traduit par une baisse de pression et une contraction par une augmentation de pression, ce qui mène à des oscillations (oscillations qu'on observe sur des étoiles réelles!) : trop de pression -> expansion -> baisse de pression -> pression insuffisante -> contraction -> hausse de pression -> trop de pression -> expansion -> etc.
Mais la pression compte dans le tenseur énergie-impulsion. Et dans le mauvais sens, c'est à dire qu'en termes newtonniens elle génère un champ de gravitation attractif supplémentaire qui s'oppose à l'effet répulsif habituel de la pression. Pour un astre gazeux, on peut montrer que si son rayon passe en dessous de 9rs/8, l'augmentation de pression ne permet plus la dilatation mais au contraire cause une contraction qui ne peut plus s'arrêter.
Il y a donc un mécanisme qui mène inexorablement à la formation d'un horizon pourvu qu'un astre gazeux deviennent assez compact. Reste à voir comment amener un astre à la compacité 8/9 et cela est d'autant plus facile qu'on considère une grande masse. Pour un truc comme M87*, il s'agit juste d'avoir une densité de l'ordre de celle l'air, donc il n'y a pas vraiment de doute quand à sa nature et à la formation d'un horizon dans le cadre de la relativité générale. Mais même pour des trucs beaucoup plus petit, comme une étoile à neutron, on a établi qu'au dessus d'une certaine masse (la limite de Tolman-Openheimer-Volkov) l'effondrement de la matière neutronique était inexorable.
Bref, sauf falsification de la relativité générale dans ce domaine de forte compacité, il y a forcément des astres qui vont s'effondrer et des horizons qui vont se former et donc des régions de l'espace-temps qui sont bien approximées par la région II. Dit autrement, la relativité générale prédit que de telles régions peuvent se former dans l'univers réel. C'est beaucoup moins évident et beaucoup plus spéculatif pour de la région IV ou pour un pont de Rosen...
m@ch3Never feed the troll after midnight!
- 28/08/2021, 11h11 #67bernarddo
- Date d'inscription
- septembre 2013
- Messages
- 195
Re : Jamais rien ne tomba dans un trou noir ?
Bonjour à tous
J’avoue, au contraire de Mailou, n’avoir rien compris à ce discours, avec ce qui me paraît être des assimilations entre choses qui ne sont pas de même nature.Je reprécise que R est le rayon aréal qu'on note r habituellement et que r est "autre chose". En passant de R (le rayon aréal, variable radiale "habituelle") à r, ça va jouer significativement sur environ 3-4 fois rs, en effet, R et r sont égaux à moins d'un demi pourcent près pour R=4rs ou plus. La partie allant de R=rs à R~4rs va se retrouver dilatée suivant l'axe horizontal pour couvrir l'intervalle r=0 à r~4rs. Tu peux jeter un oeil à ce graphe desmos : https://www.desmos.com/calculator/l4uhtwsxhu
m@ch3
Un rayon, fut-il aréal est un rayon et doit donc posséder une valeur mesurable, et quelle que soit la désignation dont on l’affuble, ce n’est pas une coordonnée qui, elle, est un marqueur, d’espace en l’occurrence, un scalaire. Quand à savoir ce qui est simplement « autre chose », on peut tout envisager…
Mais mes limites sont bien connues ici...
Heureusement il y a le schéma de correspondance entre r et R, (merci de m’avoir fait connaître desmos ), et qui va me permettre d’illustrer simplement la réelle différence entre la solution de Schwarzschild, dont on saisit bien la logique, et la solution académique qui vous entraîne dans des considérations sans fin dont je retiens simplement qu’elles ne portent que sur des représentations que l’on cherche à toute force à faire coller à la réalité, alors qu’elles la maltraitent, en introduisant des portions de coordonnées spatiales imaginaires.
), et qui va me permettre d’illustrer simplement la réelle différence entre la solution de Schwarzschild, dont on saisit bien la logique, et la solution académique qui vous entraîne dans des considérations sans fin dont je retiens simplement qu’elles ne portent que sur des représentations que l’on cherche à toute force à faire coller à la réalité, alors qu’elles la maltraitent, en introduisant des portions de coordonnées spatiales imaginaires.
Voici ce qu’il devient dans la solution de Schwarzschild
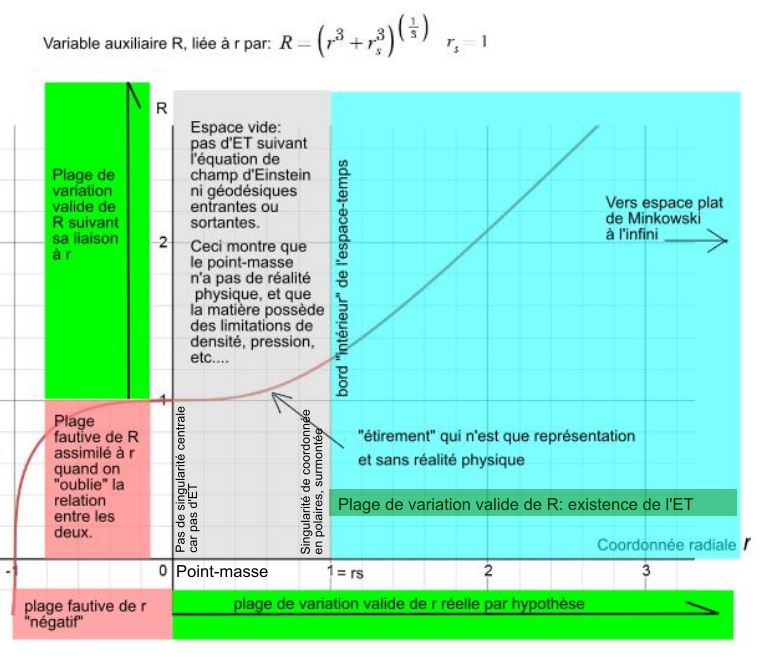
Et dans le message d’où est tiré ce paragraphe, je trouve un autre passage qui me pose problème.
Rien de bien intéressant ou utile a priori. Schwarzschild a fait l'hypothèse d'un point masse localisé en x=y=z=0, donc dans ce repère x,y,z une tranche d'espace doit tout remplir sauf ce point central. Manque de bol ce point est une sphère de rayon rs (il "suffit" de lire la métrique pour le conclure), donc la conclusion contredit l'hypothèse faite (mais il n'y avait aucun moyen de deviner qu'un point masse n'était pas possible).
Rien dans l’hypothèse de Schwarzschild n’oblige à ce que l’intégralité de l’espace soit rempli, ce qui est une exigence à priori. Son calcul montre d’ailleurs le contraire. C’est la lecture fautive de ce calcul, et le non respect de ses hypothèses qui ne permet pas de comprendre que l’existence d’astres à densité infinie, qu’il est toujours possible d’envisager en tant qu’expériences mentales et exercices mathématiques, n'est pas permise mathématiquement dans notre espace-temps, ET que de tels astres tiennent à distance.
Mais ça, ça bouscule toute la cosmologie classique…
De la même façon que dire qu’un point masse n’est pas possible, dans le sens où l’envisager n’aurait aucun sens, supprimerait de fait aux maths toutes les riches considérations que l’on peut faire sur les rapports entre les divers niveaux de zéros et d’infinis, et les possibilités de neutraliser les indéterminations qu’ils induisent, et dont on a ici un magnifique exemple.
- 01/09/2021, 14h23 #68mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
Le terme rayon aréal d'une sphère est trompeur car en dehors de la représentation il n'y a pas forcément de "rayon" dans le sens distance à un centre de cette sphère, étant donné que le centre d'une sphère d'une variété n'est pas forcément dans cette variété. Qui plus est, la variation de ce rayon aréal le long d'une ligne ne correspond même pas à la longueur de cette ligne.Un*rayon, fut-il aréal est un rayon et doit donc posséder une valeur mesurable, et quelle que soit la désignation dont on l’affuble, ce n’est pas une coordonnée qui, elle, est un marqueur, d’espace en l’occurrence, un*scalaire. Quand à savoir ce qui est simplement « autre chose », on peut tout envisager…
Un exemple simple avec une dimension de moins est une variété ressemblant à un diabolo et que vous connaissez bien ( https://blogs.futura-sciences.com/e-...paraboloid.jpg ) : si on le représente plongé dans l'espace 3D, les centres des cercles sont sur l'axe de révolution qui n'appartient pas à la variété, mais cela n'empêche pas de parler d'un équivalent de rayon pour un de ces cercles au sein même de la variété, non pas comme une distance à un centre qui n'aurait aucun sens, mais en rapport avec son périmètre qui lui est bien défini. Et quand on va d'un cercle de rayon du diabolo à un cercle de rayon
du diabolo à un cercle de rayon  en gardant la variable angulaire constante on a certainement pas parcouru la distance
en gardant la variable angulaire constante on a certainement pas parcouru la distance  .
.
Bref, il s'agit bien d'une coordonnée (d'ailleurs tout champ scalaire peut servir de coordonnée) et par défaut elle est arbitraire et n'a pas, a priori, de sens physique. C'est l'étude de la métrique exprimée dans un système de coordonnée qui permet de donner, éventuellement, un sens physique à une coordonnée.
Concernant le rayon aréal dans la métrique en coordonnées de Schwarzschild, ou de l'autre, le petit r, il ne s'agit pas, dans une coupe à t constant, de distances à un centre, tout simplement parce que le coefficient devant le ou le
ou le  n'est pas une constante. Il faut écrire la métrique en coordonnées de Gullstrand-Painlevé pour que le rayon aréal corresponde, dans une coupe à
n'est pas une constante. Il faut écrire la métrique en coordonnées de Gullstrand-Painlevé pour que le rayon aréal corresponde, dans une coupe à  constant (la coordonnée temporelle de Painlevé), à la distance à un centre, car alors le coefficient devant
constant (la coordonnée temporelle de Painlevé), à la distance à un centre, car alors le coefficient devant  vaut 1 et si on intègre l'intervalle le long d'une ligne avec
vaut 1 et si on intègre l'intervalle le long d'une ligne avec  ,
,  et
et  constant, on obtient directement la variation de
constant, on obtient directement la variation de  le long de cette ligne (d'ailleurs les coupes à
le long de cette ligne (d'ailleurs les coupes à  constant sont euclidiennes). Le changement de coordonnées allant de Schwarzschild à Gullstrand-Painlevé illustre d'ailleurs que l'espace-temps ne s'arrête pas en
constant sont euclidiennes). Le changement de coordonnées allant de Schwarzschild à Gullstrand-Painlevé illustre d'ailleurs que l'espace-temps ne s'arrête pas en  .
.
On peut d'ailleurs noter que Schwarzschild décide d'interdire les termes "rectangles" du genre (
( étant une coordonnée spatiale générique non définie) dans sa résolution ( le (2) :
étant une coordonnée spatiale générique non définie) dans sa résolution ( le (2) :  ), ce qui avec le recul n'est pas entièrement justifié.
), ce qui avec le recul n'est pas entièrement justifié.
En effet, si on opte pour des coordonnées spatiales sphériques, avec une coordonnée de type radial (r ou R peu importe ici) et deux de type angulaire et
et  et qu'on demande une symétrie sphérique, il est logique de demander l'absence des termes rectangles en
et qu'on demande une symétrie sphérique, il est logique de demander l'absence des termes rectangles en  et
et  car cela permet de rendre la symétrie sphérique directement lisible (on n'est pas obligé, mais ce serait vraiment se compliquer la vie pour rien). Par contre il n'y a pas d'argument vraiment pertinent pour exiger l'absence du terme rectangle en
car cela permet de rendre la symétrie sphérique directement lisible (on n'est pas obligé, mais ce serait vraiment se compliquer la vie pour rien). Par contre il n'y a pas d'argument vraiment pertinent pour exiger l'absence du terme rectangle en  .
.
D'ailleurs, si on considère un terme rectangle de coefficient non nul pour la résolution, on obtient directement une famille d'expressions de la métrique de Schwarzschild dans tout un tas de systèmes de coordonnées différents, famille comprenant l'expression de Schwarzschild (la seule sans terme en
de coefficient non nul pour la résolution, on obtient directement une famille d'expressions de la métrique de Schwarzschild dans tout un tas de systèmes de coordonnées différents, famille comprenant l'expression de Schwarzschild (la seule sans terme en  et probablement la seule avec un "problème" en
et probablement la seule avec un "problème" en  ), celle de Gullstrand-Painlevé, et plein d'autres. Physiquement, la nullité du coefficient devant le terme en
), celle de Gullstrand-Painlevé, et plein d'autres. Physiquement, la nullité du coefficient devant le terme en  ne fait que garantir que la vitesse coordonnée radiale de la lumière ne dépend pas de son sens (centripète ou centrifuge), or il n'y a pas de raison autres qu'arbitraire pour un tel choix. En effet le fait que la vitesse coordonnée de la lumière dépende du sens n'implique nullement que la vitesse mesurée physiquement de la lumière dépende du sens. Mais cette indépendance de la physique au système de coordonnées n'apparaissait clairement pour personne à l'époque, c'était un peu nouveau (il semble que même Painlevé n'y a rien compris, il apparait convaincu que sa solution est différente physiquement de celle de Schwarzschild, alors que si on fait des prédictions physiques avec l'une ou avec l'autre on obtient bien exactement la même chose...).
ne fait que garantir que la vitesse coordonnée radiale de la lumière ne dépend pas de son sens (centripète ou centrifuge), or il n'y a pas de raison autres qu'arbitraire pour un tel choix. En effet le fait que la vitesse coordonnée de la lumière dépende du sens n'implique nullement que la vitesse mesurée physiquement de la lumière dépende du sens. Mais cette indépendance de la physique au système de coordonnées n'apparaissait clairement pour personne à l'époque, c'était un peu nouveau (il semble que même Painlevé n'y a rien compris, il apparait convaincu que sa solution est différente physiquement de celle de Schwarzschild, alors que si on fait des prédictions physiques avec l'une ou avec l'autre on obtient bien exactement la même chose...).
Bon, sinon, moi je veux bien continuer à vous expliquer des trucs, mais de votre côté il faut arrêter de rejeter quelque chose qui est accepté consensuellement depuis des décennies alors que vous admettez vous même que vous êtes un incapable en la matière. Le nawak ça commence à bien faire.
m@ch3Never feed the troll after midnight!
- 07/09/2021, 12h03 #69mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
Un autre point m'ennuyait dans la résolution que fait Schwarzschild dans son papier et j'ai fini par trouver des informations.
En effet, Karl s'oblige à respecter , autrement dit un déterminant constant de 1 en valeur absolue pour la métrique or cela ne correspond à rien physiquement parlant. Le déterminant de la métrique n'est pas un invariant, il dépend du choix de coordonnées que l'on effectue (par exemple, en géométrie euclidienne 2D, le déterminant de la métrique vaut 1 quand on prend des coordonnées cartésiennes et r² quand on prend des coordonnées polaires).
, autrement dit un déterminant constant de 1 en valeur absolue pour la métrique or cela ne correspond à rien physiquement parlant. Le déterminant de la métrique n'est pas un invariant, il dépend du choix de coordonnées que l'on effectue (par exemple, en géométrie euclidienne 2D, le déterminant de la métrique vaut 1 quand on prend des coordonnées cartésiennes et r² quand on prend des coordonnées polaires).
J'ai fini par trouver un cours de t'Hooft (parmi les plus grosses tronches de la physique moderne pour rappel) qui dit en note de bas de page :
Le gras est de moi. Schwarzschild ne savait pas vraiment ce qu'il faisait à l'époque (et Einstein non plus). C'était pas mûr tout ça. Envoyé par t'Hooft, note de bas de page 9, page 49 "In his original paper, using a slightly different notation, Karl Schwarzschild replaced ... by a new coordinate r that vanishes at the horizon, since he insisted that what he saw as a singularity should be at the origin, claiming that only this way the solution becomes "eindeutig" (unique), so that you can calculate phenomena such as the perihelion movement (see Chapter 12) unambiguously. The substitution had to be of this form as he was using the equation that only holds if g = 1 . He did not know that one may choose the coordinates freely, nor that the singularity is not a true singularity at all. This was 1916. The fact that he was the first to get the analytic form, justifies the name Schwarzschild solution."
Envoyé par t'Hooft, note de bas de page 9, page 49 "In his original paper, using a slightly different notation, Karl Schwarzschild replaced ... by a new coordinate r that vanishes at the horizon, since he insisted that what he saw as a singularity should be at the origin, claiming that only this way the solution becomes "eindeutig" (unique), so that you can calculate phenomena such as the perihelion movement (see Chapter 12) unambiguously. The substitution had to be of this form as he was using the equation that only holds if g = 1 . He did not know that one may choose the coordinates freely, nor that the singularity is not a true singularity at all. This was 1916. The fact that he was the first to get the analytic form, justifies the name Schwarzschild solution."
m@ch3Dernière modification par mach3 ; 07/09/2021 à 12h05.
Never feed the troll after midnight!
- 11/10/2021, 16h49 #70bernarddo
- Date d'inscription
- septembre 2013
- Messages
- 195
Re : Jamais rien ne tomba dans un trou noir ?
Rebonjour, mach 3
Après avoir beaucoup réfléchi, je pense avoir déterminé le fond de notre désaccord.
Ce serait que, en cosmologiste « moderne », quand vous vous référez aux propriètés générales des variétés, vous vous référez indiscutablement à la vision actuelle de la covariance générale telle qu’elle est définie par Wikipédia :
« En physique théorique, la covariance générale (ou invariance générale) est l'invariance de la forme des lois physiques dans toute transformation de coordonnées différentiable. Le principe qui sous-tend cette notion est qu'il n'existe a priori aucune coordonnée dans la Nature, ce sont seulement des artifices mathématiques utilisés pour la décrire, et qui ne devraient donc jouer aucun rôle dans l'expression des lois fondamentales de la physique. En d'autres termes, selon le principe qui sous-tend la notion de covariance générale, les lois physiques ne portent pas a priori directement sur la Nature mais sur une variété différentielle abstraite ».
Ainsi, quand vous écrivez,
vous avez évidemment raison.
Dans le même post vous affirmez, en plein accord avec la phrase précédente, (qui, dans le post suit la nouvelle citation)
là, précisément, vous divergez de l’avis de Schwarzschild, (et du mien, ce qui n’est certes que peu important).
Pourtant, Karl avait justifié son choix de coordonnées polaires spécifiques par le besoin de conserver la valeur unitaire du déterminant dans son changement de variables.
DetA.JPG
Et il introduit, par un calcul élémentaire, de nouvelles variables du type polaire, respectant le principe de conservation des volumes
Det B.JPG
Avant d’affirmer que Karl ne savait pas ce qu’il faisait, il aurait fallu lire sa justification, et au besoin la démonter si elle n’était pas justifiée. A ma connaissance, cela n’a été fait par personne !
Mais alors, qu’est-ce qui a changé chez les cosmologistes modernes ?
Tout simplement est arrivé le principe de généralisation de la notion de covariance, suivant lequel, et Wikipédia l’explique clairement, les lois de la physique peuvent porter sur des constructions mathématiques inconnues dans la nature, autrement dit n’existant pas dans le réel.
Ce qui explique que le choix arbitraire de coordonnées n’est pas possible si on veut, comme Schwartzschild, limiter l’application des lois physiques au réel.
Les arguments purement mathématiques sur toutes variétés différentiables, recevables globalement, ne le sont plus forcément quand on se limite au réel. Lorsque, comme ici, c’est le cas, il est sûr qu’ils réclament des trésors d’abstraction qui ne sont pas à la portée de tout le monde, (en tout cas pas de moi), et l’incertitude générale du discours, les « maladresses » et l’ambigüité du vocabulaire montrent que tout ceci n’est pas franchement assimilé.
Nota : la réserve sur l’absence de termes en dr.dt est certes recevable puisque ces termes croisés respectent les conditions de symétrie sphérique et d’indépendance temporelle. Cependant, il en est exactement de même pour la solution de Hilbert, et elle ne peut donc être retenue dans la comparaison !
Encore un point intéressant : Christian Corda qui prétend tirer l’affaire au clair, et tient pour l’identité des deux métriques, fait la même lecture des résultats que Abrams qui parle de l’erreur de Hilbert :
Corda: “A clarification on the debate on “the original Schwarzschild solution”
https://arxiv.org/pdf/1010.6031.pdf (v5 2011)
Son argumentaire : dans la conclusion
…hypothesis which assumes arches of circumference to be not 2πr, but deformed by the presence of the mass of the central body M. This assumption enables the origin of the coordinate system to be not a single point, but a spherical surface having radius equal to the gravitational radius, i.e. the surface of the Schwarzschild sphere…
Argumentaire de Abrams, qui prend le contrepied
“Black Holes: The Legacy of Hilbert's Error”
arXiv:gr-qc/0102055
… l’affirmation de Hilbert est invalide. Comme résultat, dans chaque section spatiale de l’espace-temps de Hilbert, la limite (r∗ = α) correspondant à r = 0 n’est plus un point mais une sphère bidimensionnelle et par conséquent pas une singularité quasi régulière. Cela rend son espace-temps analytiquement extensible, et, comme l’ont montré Kruskal et Fronsdal, son extension maximale contient un trou noir. Le trou noir Kruskal-Fronsdal n’est donc rien de plus qu’un produit de l’ erreur de Hilbert.
On voit bien que la constatation est absolument identique, et l’hypothèse de Corda, comme son nom l’indique, reste une hypothèse, et ne reçoit pas l’ombre d’une justification dans son papier !!
Comment peut-on envisager que l’origine d’un système d’axes que Schwarzschild a placé dans l’espace réel, (et dans lequel elle est forcément ponctuelle), puisse se retrouver sur une sphère bidimensionnelle, forcément imaginaire !!
- 15/10/2021, 17h38 #71mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
J'ai trouvé le pourquoi du déterminant de la métrique de -1 :
https://physics.stackexchange.com/qu...field-equation
C'est simplement pour rendre l'équation d'Einstein plus simple et rendre la résolution plus facile. C'est clair que pour m'y être essayé, exprimer les composantes du tenseur de Ricci à la main, c'est très fastidieux, même avec une situation très symétrique comme c'est le cas ici. Si on impose un déterminant de la métrique à -1 alors on a plus que la moitié du travail à faire (la moitié des termes du tenseur de Ricci disparaissent).
Pas le temps pour en dire plus ou commenter le message précédent.
m@ch3Never feed the troll after midnight!
- 18/10/2021, 16h54 #72mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
On peut remonter d'un cran dans les sources :
https://en.wikisource.org/wiki/Trans...of_Gravitation
traduction : le système de coordonnées doit être choisi pour respecter la règle simple que Envoyé par Albert Einstein, The Field Equations of Gravitation (1915) The coordinate system had to be specialized in accordance with the simple rule, that
Envoyé par Albert Einstein, The Field Equations of Gravitation (1915) The coordinate system had to be specialized in accordance with the simple rule, that is made to 1, whereby the equations of the theory experience an eminent simplification
is made to 1, whereby the equations of the theory experience an eminent simplification vaille 1, afin que les équations de la théorie subissent une éminente simplification
vaille 1, afin que les équations de la théorie subissent une éminente simplification
Einstein et Schwarzschild savaient donc que ne valait pas forcément 1, mais ils ont choisi sciemment cette valeur pour faciliter la résolution (la moitié des termes de l'équation du champ disparaissent). C'est une commodité, pas un choix physique. Une fois la résolution faite dans ce système de coordonnées particulier, on peut changer de système de coordonnées à loisir. On montre par ailleurs facilement que la résolution (plus difficile à la main, mais aujourd'hui on a des programmes de calcul formel) dans un système avec
ne valait pas forcément 1, mais ils ont choisi sciemment cette valeur pour faciliter la résolution (la moitié des termes de l'équation du champ disparaissent). C'est une commodité, pas un choix physique. Une fois la résolution faite dans ce système de coordonnées particulier, on peut changer de système de coordonnées à loisir. On montre par ailleurs facilement que la résolution (plus difficile à la main, mais aujourd'hui on a des programmes de calcul formel) dans un système avec  différent de 1 donne bien la même solution.
différent de 1 donne bien la même solution.
m@ch3Never feed the troll after midnight!
- 19/10/2021, 13h41 #73mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
Donc là, pour le coup, je me suis planté, Karl savait ce qu'il faisait. Je ne connaissais pas cette simplification de l'équation du champ, simplification à laquelle je n'avais pas fait attention dans mes lectures précédentes du papier. J'avais cru qu'il était écrit que le tenseur de Ricci était nul, alors qu'il manque la moitié des termes pour que ce soit le tenseur de Ricci. Du coup quand Karl dit que pour preserver l'écriture de l'équation du champ, il faut g=1, et bien c'était incompréhensible, parce que écrit sous la forme Ricci=0, l'équation du champ ne dépend pas de la valeur de g. Evidemment, comme il s'agit d'une écriture simplifiée qui sépare le tenseur de Ricci en deux morceaux dont l'un s'annule uniquement si g=1, je comprends maintenant parfaitement pourquoi il dit que l'écriture de l'équation du champ n'est préservée que si g=1.Ainsi, quand vous écrivez,
vous avez évidemment raison.
Dans le même post vous affirmez, en plein accord avec la phrase précédente, (qui, dans le post suit la nouvelle citation)
là, précisément, vous divergez de l’avis de Schwarzschild, (et du mien, ce qui n’est certes que peu important).
Pourtant, Karl avait justifié son choix de coordonnées polaires spécifiques par le besoin de conserver la valeur unitaire du déterminant dans son changement de variables.
Pièce jointe 447254
Et il introduit, par un calcul élémentaire, de nouvelles variables du type polaire, respectant le principe de conservation des volumes
Pièce jointe 447255
Avant d’affirmer que Karl ne savait pas ce qu’il faisait, il aurait fallu lire sa justification, et au besoin la démonter si elle n’était pas justifiée. A ma connaissance, cela n’a été fait par personne !
Comme je l'ai dit dans mon post précédent, la motivation de Karl à imposer g=1 n'était aucunement le sens physique, mais la simplification des calculs.
Concernant la covariance générale, je propose de rester formel plutot que de commenter des phrases littéraires d'un genre douteux comme celle du wiki français (absente par ailleurs de la version anglaise alors que le reste du paragraphe est présent) : "En d'autres termes, selon le principe qui sous-tend la notion de covariance générale, les lois physiques ne portent pas a priori directement sur la Nature mais sur une variété différentielle abstraite".
La covariance générale c'est le fait que les lois physiques sont des relations entre tenseurs et donc que leur forme ne dépend pas du système de coordonnées, mieux encore, elles s'expriment en l'absence de la définition d'un système de coordonnées. On peut faire toute la physique sans système de coordonnées (tout comme on peut faire de la géométrie euclidienne sans système de coordonnées), c'est juste que sans l'outil extraordinairement puissant que représentent les systèmes de coordonnées, c'est incroyablement plus difficile (et donc faire sans, à part pour le défi ou l'éducation, c'est possiblement juste une perte de temps idiote).
Les lois de la physique portent bien sur le réel, c'est leur rôle. Ce qui les valide c'est l'accord entre les observations faites dans le monde réel et les prédictions qu'elles font, et ce qui les rend encore plus utile c'est qu'elles peuvent prédire du réel non encore observé (neptune, les ondes electromagnétiques, les lasers, les ondes gravitationnelles, j'arrête là, la liste est longue).
Certes, pour se faire, on calque sur le réel un modèle mathématique qui a toutes les chances d'être plus étendu que le réel qu'il semble devoir décrire, mais la délimitation n'a rien d'évident. Ce n'est pas parce que le modèle va au-delà ce qu'on connait du réel à un instant donné qu'il faut décrété que tout ce qui dépasse est erroné (à moins d'avoir une très bonne raison). Ce serait une erreur grave. Par exemple aux débuts de l'electrodynamique quantique, Dirac était bien embêté avec des électrons d'énergie négative. Il aurait pu simplement se dire, ben comme on n'observe pas d'électron d'énergie négative, on n'a qu'à simplement ignorer ces solutions parce que le modèle va trop loin. Finalement, il a prédit l'existence du positron et on l'a découvert.
Si. On fait ce qu'on veut avec les coordonnées. Il ne faut pas confondre les coordonnées et les grandeurs physiques mesurées. Concrétement une grandeur physique ce sera le résultat d'une opération entre tenseurs qui peut s'écrire en l'absence de la définition d'un système de coordonnées. La confusion vient du fait qu'en physique classique il est simple et évident d'associer les coordonnées à des grandeurs physiques (des distances, des durées, éventuellement des angles) et qu'il ne viendrait pas à l'idée d'utiliser un système de coordonnées arbitraire non associé à des grandeurs physique en physique classique car cela ne ferait que compliquer les calculs de façon inutile. Or, en relativité générale, il n'y a plus de façon simple et évidente de faire la même association. Aucun système de coordonnée ne pourra avoir toutes les "bonnes" propriétés en même temps, il y aura forcément un truc qui merde (sauf si l'espace-temps est plat) et qui sera contre-intuitif. Par exemple dans le système de coordonnées de Schwarzschild, la coordonnée radiale de Schwarzschild (n'importe laquelle des deux r ou R) n'est pas une distance à un centre, car le coefficient devant dr² ou dR² n'est pas 1 (ou -1, en fonction de la convention).
On parlera de Corda après, il faut que je lise son papier d'abord.
m@ch3Never feed the troll after midnight!
- 20/10/2021, 13h42 #74mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
J'ai diagonalisé Corda et c'est un bon papier.
Concernant Abrams, obscur personnage (apparemment seulement 4 publications, toutes sur Schwarzschild, probablement un doctorat mais dont il est impossible de savoir dans quelle spécialité, pas de traces de postes dans des établissement de recherche, apparemment un passage chez Lookheed, il serait décédé en 2001, à part ça très peu d'informations), les erreurs qu'il commet dans ses écrits sont décortiquées ici : http://www.internationalskeptics.com...d.php?t=231833
Pour résumer, Abrams était quelqu'un qui croyait erronément que R3 privé d'un point est topologiquement différent de R3 privé d'une boule fermé.
Pas le temps de développer plus, mais l'exploration est intéressante.
m@ch3Dernière modification par mach3 ; 20/10/2021 à 14h19. Motif: "sphère" corrigé en "boule fermée", merci pm42, au moins il y en a qui suivent :)
Never feed the troll after midnight!
- 20/10/2021, 13h50 #75Deedee81
- Date d'inscription
- octobre 2007
- Localisation
- Courcelles - Belgique
- Âge
- 63
- Messages
- 47 509
Re : Jamais rien ne tomba dans un trou noir ?
Dernière modification par mach3 ; 20/10/2021 à 14h20. Motif: "sphère" corrigé en "boule fermée", merci pm42, au moins il y en a qui suivent :)
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
- 20/10/2021, 14h00 #76pm42
- Date d'inscription
- juillet 2015
- Messages
- 15 279
Re : Jamais rien ne tomba dans un trou noir ?
En lisant le texte anglais, ils disent "entire closed ball" et je pense que c'est "boule" plutôt que "sphère". Si on retire une sphère de R3, c'est à dire juste la frontière de la boule, on se retrouve avec 2 espaces séparés et l'ensemble n'est plus connexe par ex.
Je peux me tromper ceci dit, cela fait quelque décennies que je n'ai plus fait de topologie.Dernière modification par pm42 ; 20/10/2021 à 14h01.

- 20/10/2021, 14h10 #77mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
non, c'est bien une boule fermée (donc une sphère + son contenu). Merci d'avoir relever. Je vais corriger.En lisant le texte anglais, ils disent "entire closed ball" et je pense que c'est "boule" plutôt que "sphère". Si on retire une sphère de R3, c'est à dire juste la frontière de la boule, on se retrouve avec 2 espaces séparés et l'ensemble n'est plus connexe par ex.
Je peux me tromper ceci dit, cela fait quelque décennies que je n'ai plus fait de topologie.Never feed the troll after midnight!
- 20/10/2021, 14h14 #78Deedee81
- Date d'inscription
- octobre 2007
- Localisation
- Courcelles - Belgique
- Âge
- 63
- Messages
- 47 509
Re : Jamais rien ne tomba dans un trou noir ?
J'avais aussi "traduit" inconsciemment. C'est fou ça !
"Il ne suffit pas d'être persécuté pour être Galilée, encore faut-il avoir raison." (Gould)
- 22/10/2021, 19h07 #79bernarddo
- Date d'inscription
- septembre 2013
- Messages
- 195
Re : Jamais rien ne tomba dans un trou noir ?
Bonjour,
Tout ces rebondissements sur les mérites respectifs de Abrams ou Corda sont très intéressants, mais je n’avais cité leurs travaux respectifs que pour signaler que, à la lumière de la même lecture (factuelle) qu'ils avaient fait tiré de la démonstration de Hilbert , ils avaient tiré des conclusions opposées, et ne doivent pas nous écarter de l’examen du papier de Schwarzschild !
Certainement plus intéressante est la découverte par mach3, d’une justification par objectif de simplification du calcul, du choix fait par Schwarzchild de fixer à 1 la valeur absolue du déterminant de G.
(A noter qu’on trouvait déjà ce choix dans la solution de Einstein de novembre 1915)
Cependant, il ne s’agit que de la moitié de son argumentaire particulier.
L’autre moitié, et ce qui fait l’autre singularité de sa démonstration c’est son affirmation que « les équations de champ … ont la propriété fondamentale de conserver leur forme dans tout système de coordonnées (ici, polaire par exemple), à la condition que le déterminant de son changement de variables (à partir d’un système initial ici cartésien) soit égal à 1. »
…et qui le conduit à faire ce changement de variables simple, dont on voit bien qu’il réalise effectivement cette conservation de forme sur l’élément de volume qui s’exprime ainsi identiquement comme produit des accroissements élémentaires dans les deux systèmes de coordonnées, élément réel de la partie espace de l’ET, qui fait que ce choix est nécessaire et l’amène à cette solution simple, unique, dépourvue de singularité, et qui fait donc sens en affectant des limites physiques à la fois aux particules, et aux propriétés physiques en général.
Et il est ensuite logique qu’il en soit de même pour l’élément de géodésique (lui aussi physique ou réel) qui fait l’objet du calcul (et qui est en fait une sorte de théorème de Pythagore local généralisé)
On peut donc être d’accord avec l’affirmation suivante
Il semblerait que la bonne raison existe et ait été exposée (et exploitée) par Schwarzschild, puis oubliée !!Les lois de la physique portent bien sur le réel, c'est leur rôle. Ce qui les valide c'est l'accord entre les observations faites dans le monde réel et les prédictions qu'elles font, et ce qui les rend encore plus utile c'est qu'elles peuvent prédire du réel non encore observé (neptune, les ondes electromagnétiques, les lasers, les ondes gravitationnelles, j'arrête là, la liste est longue).
Certes, pour se faire, on calque sur le réel un modèle mathématique qui a toutes les chances d'être plus étendu que le réel qu'il semble devoir décrire, mais la délimitation n'a rien d'évident. Ce n'est pas parce que le modèle va au-delà ce qu'on connait du réel à un instant donné qu'il faut décrété que tout ce qui dépasse est erroné (à moins d'avoir une très bonne raison). Ce serait une erreur grave
C’est probablement dans sa justification qu’il faut donc chercher le bon choix. Ce n’est certes pas dans mes cordes.
- 25/10/2021, 14h34 #80mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
Il y a un problème de compréhension manifeste. Je vais donc la refaire, en plus détaillé. L'équation du champ d'Einstein (en omettant le terme lié à la constante cosmologique et dans un système d'unités tel que G=c=1), est la suivante :Certainement plus intéressante est la découverte par mach3, d’une justification par objectif de simplification du calcul, du choix fait par Schwarzchild de fixer à 1 la valeur absolue du déterminant de G.
(A noter qu’on trouvait déjà ce choix dans la solution de Einstein de novembre 1915)
Cependant, il ne s’agit que de la moitié de son argumentaire particulier.
L’autre moitié, et ce qui fait l’autre singularité de sa démonstration c’est son affirmation que « les équations de champ … ont la propriété fondamentale de conserver leur forme dans tout système de coordonnées (ici, polaire par exemple), à la condition que le déterminant de son changement de variables (à partir d’un système initial ici cartésien) soit égal à 1. »
 ,
,
Avec le tenseur de Ricci (forme bilinéaire symétrique transformant un couple de vecteurs en scalaire),
le tenseur de Ricci (forme bilinéaire symétrique transformant un couple de vecteurs en scalaire),  le scalaire de Ricci qui est une contraction du tenseur de Ricci sur le tenseur métrique inverse (au lieu de deux vecteurs, on met en entrée du Ricci le tenseur métrique inverse pour obtenir un scalaire) et
le scalaire de Ricci qui est une contraction du tenseur de Ricci sur le tenseur métrique inverse (au lieu de deux vecteurs, on met en entrée du Ricci le tenseur métrique inverse pour obtenir un scalaire) et  le tenseur métrique (autre forme bilinéaire symétrique transformant un couple de vecteurs en scalaire), l'ensemble formant le tenseur d'Einstein,
le tenseur métrique (autre forme bilinéaire symétrique transformant un couple de vecteurs en scalaire), l'ensemble formant le tenseur d'Einstein,  , qui est égal (à la constante multiplicative
, qui est égal (à la constante multiplicative  près) à
près) à  , le tenseur énergie-impulsion (également une forme bilinéaire symétrique transformant un couple de vecteurs en scalaire).
, le tenseur énergie-impulsion (également une forme bilinéaire symétrique transformant un couple de vecteurs en scalaire).
Si le nombre de dimension est 4, alors on peut écrire de façon équivalente :

où (ne pas confondre avec
(ne pas confondre avec  qui est en gras bien que l'éditeur LaTeX du forum ne permette pas forcément une bonne distinction) est le scalaire énergie-impulsion qui est une contraction du tenseur énergie-impulsion sur le tenseur métrique inverse (au lieu de deux vecteurs, on met en entrée du tenseur énergie-impulsion le tenseur métrique inverse pour obtenir un scalaire).
qui est en gras bien que l'éditeur LaTeX du forum ne permette pas forcément une bonne distinction) est le scalaire énergie-impulsion qui est une contraction du tenseur énergie-impulsion sur le tenseur métrique inverse (au lieu de deux vecteurs, on met en entrée du tenseur énergie-impulsion le tenseur métrique inverse pour obtenir un scalaire).
Lorsque l'on considère une région vide de l'espace-temps, le tenseur énergie-impulsion et le scalaire associé sont nuls. L'équation du champ à satisfaire est donc :
 , ce qui signifie que peu importe les deux vecteurs que l'on met en entrée du tenseur de Ricci, on obtiendra 0 comme scalaire en sortie
, ce qui signifie que peu importe les deux vecteurs que l'on met en entrée du tenseur de Ricci, on obtiendra 0 comme scalaire en sortie
Pour procéder à la résolution de manière commode, il faut travailler avec des composantes. On choisit donc 4 champs scalaires, définis sur la variété de façon à ce qu'ils forment un système de coordonnées sur une région de cette variété (on prend ce qu'on veut, il faut juste qu'ils permettent une bijection entre la région de la variété et un morceau de R4). A partir de ces 4 champs scalaires, on défini 4 champs de 1-formes,
définis sur la variété de façon à ce qu'ils forment un système de coordonnées sur une région de cette variété (on prend ce qu'on veut, il faut juste qu'ils permettent une bijection entre la région de la variété et un morceau de R4). A partir de ces 4 champs scalaires, on défini 4 champs de 1-formes,  qui sont les gradients de ces champs scalaires. En chaque évènement, ces 4 1-formes forment une base qui est duale d'une autre base formée par 4 champs de vecteurs opérateurs de dérivée partielle
qui sont les gradients de ces champs scalaires. En chaque évènement, ces 4 1-formes forment une base qui est duale d'une autre base formée par 4 champs de vecteurs opérateurs de dérivée partielle  . Comme il s'agit de bases duales, on a la propriété
. Comme il s'agit de bases duales, on a la propriété  (symbole de Kroenecker valant 1 si mu=nu et 0 sinon).
(symbole de Kroenecker valant 1 si mu=nu et 0 sinon).
En chaque évènement, on peut prendre le Ricci qui s'y trouve et lui donner ces opérateurs par couples (16 couples possibles, mais il suffit de 10, par symétrie) pour qu'il les transforme en scalaires. On obtient ainsi 10 scalaires qui sont les composantes du tenseur de Ricci dans le système de coordonnées choisi :

L'équation du champ à satisfaire peut donc se réécrire sous la forme de 10 équations :

Ensuite il nous faut exprimer les composantes , grâce à la définition du tenseur de Ricci à partir du tenseur de Riemann. Le tenseur de Riemann prend en entrée une 1-forme et 3 vecteurs pour donner un scalaire en sortie (équivalemment, on peut ne lui donner que 3 vecteurs en entrée et il donner un vecteur en sortie). On défini le Ricci en contractant Riemann sur lui-même :
, grâce à la définition du tenseur de Ricci à partir du tenseur de Riemann. Le tenseur de Riemann prend en entrée une 1-forme et 3 vecteurs pour donner un scalaire en sortie (équivalemment, on peut ne lui donner que 3 vecteurs en entrée et il donner un vecteur en sortie). On défini le Ricci en contractant Riemann sur lui-même :
Pour tout vecteurs quelconques et
et  , et pour toute bases
, et pour toute bases  et sa base duale
et sa base duale  ,
,

L'équation du champ à satisfaire est maintenant :
 , avec
, avec  , des composantes du tenseur de Riemann dans le système de coordonnées choisi. Cette expression est vraie pour tout système de coordonnées.
, des composantes du tenseur de Riemann dans le système de coordonnées choisi. Cette expression est vraie pour tout système de coordonnées.
Il faut maintenant exprimer les composantes du tenseur de Riemann, et c'est ici que cela se corse, les composantes du tenseur de Riemann sont :

les étant les symboles de Christofell (équation A.3 du papier du Schwatzschild).
étant les symboles de Christofell (équation A.3 du papier du Schwatzschild).
Donc, les composantes du tenseur de Ricci sont :

Et donc l'équation du champ à résoudre devient :

Cette expression est vraie pour tout système de coordonnées. On peut démarrer la résolution à partir de là, mais c'est mission impossible si on ne choisit pas un minimum un système de coordonnée reflétant les symétries du problème. Si on n'a que du papier et un crayon et qu'on dispose de beaucoup, beaucoup, beaucoup de temps (beaucoup de temps pour calculer tous les termes à la main et beaucoup beaucoup de temps pour vérifier qu'on ne s'est pas trompé à la main, il faut se rendre compte que chaque expression développée fera plusieurs lignes !), ou si on dispose d'un ordinateur avec un logiciel de calcul formel, alors on obtient la solution au problème d'Einstein à partir de cette équation.
L'astuce de Schwarzschild (et aussi d'Einstein avant lui) qui n'avait pas d'ordinateur est de considérer des systèmes de coordonnées particulier tels que le déterminant de la métrique vaut 1, ce qui permet une simplification de l'équation, qui prend alors la forme A.4 dans son papier. Cette forme contient beaucoup moins de termes et met ainsi la résolution à la portée du calcul à la main en un temps beaucoup plus faible. Evidemment, si on ne veut pas se retrouver avec la forme générale atroce ci-dessus, on n'a plus le droit de changer de coordonnées comme on le souhaite et il faut impérativement que le déterminant de la métrique reste égal à 1 quand on fait ce changement.
Comme je l'ai déjà dit, mais il semble que cela n'a pas été bien compris, il s'agit seulement d'une commodité, pas une exigence physique. La seule et unique raison du choix d'un système de coordonnée qui donne un déterminant de 1 pour la métrique est d'avoir une forme simplifiée de l'équation du champ.
Les équations du champ générales (celle donnée ci-dessus) conservent leur forme pour tout système de coordonnées.
Les équations simplifiées (A.4) ne conservent leur forme que pour les système des coordonnées qui donnent un déterminant de 1 à la métrique.
m@ch3Never feed the troll after midnight!
- 26/10/2021, 17h01 #81bernarddo
- Date d'inscription
- septembre 2013
- Messages
- 195
Re : Jamais rien ne tomba dans un trou noir ?
Rebonjour,
Encore merci, vous venez de justifier la seconde partie de l’argumentaire comme simple conséquence de la première astuce du choix d’un système de coordonnées permettant un calcul simplifié. Mon hypothèse s'effondre donc.
Mais on va enquêter plus loin dans ce calcul astucieux:L'astuce de Schwarzschild (et aussi d'Einstein avant lui) qui n'avait pas d'ordinateur est de considérer des systèmes de coordonnées particulier tels que le déterminant de la métrique vaut 1, ce qui permet une simplification de l'équation, qui prend alors la forme A.4 dans son papier. Cette forme contient beaucoup moins de termes et met ainsi la résolution à la portée du calcul à la main en un temps beaucoup plus faible. Evidemment, si on ne veut pas se retrouver avec la forme générale atroce ci-dessus, on n'a plus le droit de changer de coordonnées comme on le souhaite et il faut impérativement que le déterminant de la métrique reste égal à 1 quand on fait ce changement.
m@ch3
J’en déduis donc que le calcul de Schwartzschild, que nul à ma connaissance n’a mis en défaut, est impeccable (et continûment astucieux) jusqu’à son obtention des expressions f1, f2 (f3) et f4, et qu’il est dans le vrai lorsqu’il en tire la conclusion qu’elles remplissent toutes les conditions de départ, excepté la condition de continuité (4) qu’il avait seul posée au départ (pour devoir être respectée partout sauf, nécessairement, au point x1 = 0, pour lequel les caractéristiques physiques de la masse ponctuelle deviennent indéterminées, induisant obligatoirement une indétermination mathématique quelque part dans les expressions en ce point)).
Le constat que l’expression f1 recèle un tel problème d’indétermination, valide l’affirmation (et l’exception qui s’y attache) de son exigence de continuité, lui permet, en ramenant cette indétermination au point (origine des coordonnées) où elle était attendue, de fixer de façon univoque la seconde constante d’intégration du calcul, sur ce qui doit être considéré comme une seconde condition aux limites, (la première ayant été fixée par la première condition aux limites, celle existant à l’infini), et assure ainsi l’unicité de sa solution. Calcul on ne peut plus banal, accessible au plus grand nombre
Bien que Karl n’ait pas éprouvé le besoin de justifier l’établissement de cette condition de continuité, (tellement elle est sous-tendue par l’ensemble des observations de notre monde et des présupposés de la science), elle peut (et à mon sens, doit) être comprise comme la condition mathématique du plongement de sa solution dans l’espace-temps physique, son unicité mathématique indiquant clairement que tout autre mode de fixation de la seconde constante d’intégration (par exemple celui de Hilbert), expulse la solution de cet espace-temps (physique, pour le territoire, et R4 en mathématiques), pour entrer dans un espace de représentation, (celui des cartes), avec toutes les distorsions et ruptures de continuités imaginables.
Celui qui donne les discussions surréalistes du type ici #62, #63 qui montrent que les esprits rationnels sont déchirés entre leur logique et la nécessité de la bousculer pour comprendre l’incompréhensible…qui résulte du choix de la solution de Hilbert !
- 28/10/2021, 15h16 #82mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
N'allons pas trop vite et suivons les étapes.
Karl démarre avec des coordonnées qu'il considère cartésiennes ("rectangular coordinates"), ce qui est un parti-pris important. Il s'agit quand même de décrire la géométrie de quelque chose qui ne peut pas comporter des coordonnées cartésiennes par définition car ce quelque chose est une variété pseudo-Riemannienne. C'est comme vouloir couvrir la surface d'une sphère avec des coordonnées cartésiennes x et y, ça peut marcher localement, mais ça va vite poser des problèmes.
Ce qui est cartésien dans les coordonnées qu'il utilise c'est la façon dont elles sont disposées dans la carte, pas dans le territoire. Karl prend R4 privé d'une ligne comme carte par défaut et choisit donc des coordonnées cartésiennes dans sa carte. On ne sait pas a priori ce que cela donne dans le territoire et trouver l'expression de la métrique permettra justement de savoir ce qu'il en est. Au mieux, la topologie du territoire sera R4 privé d'un cylindre sphérique plein (la topologie du territoire, qui est un morceau de l'espace-temps, doit correspondre à celle de la carte). On ne pourra estimer le "rayon" de ce cylindre qu'une fois l'expression de la métrique trouvée.
Autre présupposé qu'il fait concernant sa carte, elle est le produit cartésien d'une droite R (coordonnée t) et d'un espace R3 (coordonnées x,y,z) privé d'un point, et il y a une symétrie par translation et inversion suivant la droite et une symétrie sphérique (centrée sur le point manquant) dans cet espace.
Concernant les symétries de la droite :
La symétrie par translation fait que les coefficients de la métrique doivent être indépendants de la coordonnée t, en effet, son expression ne doit pas changer si on remplace t par t+K avec K une constante quelconque.
La symétrie par inversion fait que les coefficients des termes rectangles dtdx, dtdy et dtdz sont nuls afin d'avoir une expression inchangée si on change t par -t (en effet si on change t par -t, on a dt²=d(-t)² mais dtdx=-d(-t)dx, une inversion du temps inverse le signe de ces termes rectangles)
Le choix d'une symétrie par translation est assez légitime vu que Karl cherche une solution statique, avec comme a priori que t est temporel. Le choix de la symétrie par inversion tient plus de la simplicité. Après il n'y a aucune obligation formelle de respecter dans la carte les symétries du territoire. Par exemple si le territoire est le plan euclidien et que j'utilise les coordonnées polaires en mettant sur ma carte r en abscisse et theta en ordonnée, les symétries par translation du plan euclidien ne sont pas respectée dans la carte. Autre exemple, plus utile, si le territoire est la surface d'une sphère, peu importe le système de coordonnée qui sera représenté en abscisse et en ordonnée sur ma carte, il est impossible de capturer toutes les symétries : il faut choisir lesquelles sont respectées et lesquelles sont sacrifiées.
Concernant la symétrie sphérique :
Le choix est fait de respecter la symétrie sphérique dans la carte. Ainsi est créé un nouveau champ scalaire, r, tel que , le point dont on a privé la carte étant en x=y=z=0, son centre. Ce choix, qui n'est pas le seul possible (toute fonction monotone de
, le point dont on a privé la carte étant en x=y=z=0, son centre. Ce choix, qui n'est pas le seul possible (toute fonction monotone de  étant à même de remplir le même rôle), fait que, dans la carte, r est une distance euclidienne au centre de la carte (ou plutôt à un point arbitrairement proche du centre car celui-ci est exclu de la carte) et qu'une différence de r entre deux points sur la même radiale (une demi-droite de la carte dont l'origine serait le centre de la carte s'il n'était pas exclu) est la distance euclidienne entre ces deux points sur la carte. Attention, r n'est pas la distance au centre dans le territoire a priori, et une différence de r entre deux points sur la même radiale (qui n'est pas nécessairement une demi-droite et n'a pas nécessairement le centre pour origine dans le territoire) n'est pas la distance entre ces deux points a priori : cela dépendra de l'expression de la métrique qui sera obtenue (il faut, dans l'expression de la métrique, que le coefficient devant dr² soit constant et égal à 1 ou -1 pour que cela soit le cas).
étant à même de remplir le même rôle), fait que, dans la carte, r est une distance euclidienne au centre de la carte (ou plutôt à un point arbitrairement proche du centre car celui-ci est exclu de la carte) et qu'une différence de r entre deux points sur la même radiale (une demi-droite de la carte dont l'origine serait le centre de la carte s'il n'était pas exclu) est la distance euclidienne entre ces deux points sur la carte. Attention, r n'est pas la distance au centre dans le territoire a priori, et une différence de r entre deux points sur la même radiale (qui n'est pas nécessairement une demi-droite et n'a pas nécessairement le centre pour origine dans le territoire) n'est pas la distance entre ces deux points a priori : cela dépendra de l'expression de la métrique qui sera obtenue (il faut, dans l'expression de la métrique, que le coefficient devant dr² soit constant et égal à 1 ou -1 pour que cela soit le cas).
L'expression de la partie spatiale de la métrique est :

C'est astucieux, car ainsi, les indicatrices (en version 3D) représentant la métrique dans la carte sont forcément des ellipsoïdes dont l'axe de symétrie passe par l'origine. En effet, le premier terme et une métrique euclidienne, représentée sur la carte par une indicatrice sphérique et le second une métrique dégénérée, représentée sur la carte par une indicatrice ellipsoïde oblate "dégénérée" (avec deux axes de longueur infinie) orthogonale à la radiale sur laquelle elle se trouve : la somme des deux donne forcément une ellipsoïde (oblate ou prolate, en fonction des signes de G et H) dont l'axe de symétrie passe par l'origine de la carte. Pour finaliser la symétrie sphérique dans la carte, il suffit juste que G et H soient des fonctions de (et donc de r, vu qu'on l'a défini comme cela, mais toute autre fonction monotone de
(et donc de r, vu qu'on l'a défini comme cela, mais toute autre fonction monotone de  permet la symétrie sphérique dans la carte.
permet la symétrie sphérique dans la carte.
L'expression complète de la métrique à ce stade est donc :
 , avec F, G et H trois fonctions de
, avec F, G et H trois fonctions de 
Précisons en passant que F ne peut être fonction que de r (ou de toute fonction de r) pour respecter les symétries.
On peut la développer complétement :

Le déterminant de la métrique est alors (je passe le détail de ce calcul), et F, G et H sont des fonctions de r tels que ce déterminant vaut toujours -1.
(je passe le détail de ce calcul), et F, G et H sont des fonctions de r tels que ce déterminant vaut toujours -1.
On impose que l'expression de cette métrique tend vers celle de Minkowski quand r tend vers l'infini. Cela impose F=G=1 et H=0 quand r tend vers l'infini et respecte bien la condition sur le déterminant.
Marquons une pause, avant de passer aux coordonnées sphériques.
m@ch3Never feed the troll after midnight!
- 28/10/2021, 18h10 #83mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
Re,
Donc les coordonnées sphériques. On a déjà défini une coordonnée radiale, r, comme une distance euclidienne au centre de la carte (enfin, à un point arbitrairement proche du centre, ce centre étant exclu). Il ne reste qu'à définir les coordonnées angulaires et
et  , de manière usuelle :
, de manière usuelle :



Il est connu qu'avec une telle définition des coordonnées, la métrique d'Euclide s'écrit ainsi (on pourrait le redémontrer) :

par ailleurs, comme , il vient :
, il vient :

On peut donc reprendre l'expression :
:
 , avec F, G et H trois fonctions de
, avec F, G et H trois fonctions de 
et la réarranger un peu :

Dans ce nouveau système de coordonnées, le déterminant vaut . Si F, G et H respectent la condition donnée précédemment, cela nous donne un déterminant qui vaut
. Si F, G et H respectent la condition donnée précédemment, cela nous donne un déterminant qui vaut  et on ne peut plus utiliser l'équation du champ simplifiée.
et on ne peut plus utiliser l'équation du champ simplifiée.
Une première option (que Karl n'envisage même pas, on va vite voir pourquoi), c'est de rédéfinir F, G et H pour que . On aurait le droit car après tout, F, G et H ne seront déterminées qu'à la fin, mais... F, G et H ne peuvent dépendre que de r, alors qu'il faudrait une dépendance en
. On aurait le droit car après tout, F, G et H ne seront déterminées qu'à la fin, mais... F, G et H ne peuvent dépendre que de r, alors qu'il faudrait une dépendance en  d'au moins l'un d'eux pour que la condition soit respectée.
d'au moins l'un d'eux pour que la condition soit respectée.
Une deuxième option est d'inventer de nouveaux champs scalaires de manière astucieuse :



ce qui donne :



On peut substituer dans l'expression de la métrique les :
:

Dans ce nouveau système de coordonnées, le déterminant vaut de nouveau
On peut aller un peu plus loin dans les substitutions, en remarquant que :
:

Nous voici donc arrivés à l'expression A.8, qui précède la définition des f1,f2,f3 et f4. Nous allons donc entrer dans le vif du sujet, mais pas aujourd'hui.
m@ch3Never feed the troll after midnight!
- 29/10/2021, 14h21 #84mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
Re,
Karl pose à partir de là :



Ce qui donne l'écriture suivante pour la métrique :

Et là, il attaque le calcul des symboles de Christofell (par une méthode que je n'ai pas bien comprise car non détaillée, mais qui m'en rappelle une autre, il établit d'abord l'équation des géodésiques puis il en extrait les symboles) et les obtient en fonction des f et de leurs dérivées. La symétrie sphérique lui permet ensuite de ne considérer que l'équateur ( ) pour poursuivre la résolution, ce qui abouti à seulement 3 équations différentielles au lieu de 4, simplifiées car les termes en x_2 ont disparus. Il n'utilise ensuite que 2 d'entre-elles, ainsi que le fait que
) pour poursuivre la résolution, ce qui abouti à seulement 3 équations différentielles au lieu de 4, simplifiées car les termes en x_2 ont disparus. Il n'utilise ensuite que 2 d'entre-elles, ainsi que le fait que  (imposé par le déterminant qui doit valoir -1), pour résoudre. Il trouve (on passe les détails) :
(imposé par le déterminant qui doit valoir -1), pour résoudre. Il trouve (on passe les détails) :
 avec
avec  et
et  deux constantes d'intégration
deux constantes d'intégration
Il faut que G tende vers 1 quand r tend vers l'infini, donc doit tendre vers
doit tendre vers  quand
quand  tend vers l'infini. Comme
tend vers l'infini. Comme  , on a quand
, on a quand  ,
,  . Pour satisfaire la condition aux limites, on a donc
. Pour satisfaire la condition aux limites, on a donc  et :
et :

Puis il trouve :

et :

On peut donc, à ce stade, écrire l'expression suivante pour la métrique :

On constate que deux coefficients de la métrique peuvent diverger. D'abord celui devant qui diverge quand
qui diverge quand  vaut 1 ou -1, ce qui correspond à un angle
vaut 1 ou -1, ce qui correspond à un angle  valant 0 ou
valant 0 ou  . Ceci est en fait une pathologie connue des coordonnées angulaires : les pôles sont absent d'une carte qui porterait
. Ceci est en fait une pathologie connue des coordonnées angulaires : les pôles sont absent d'une carte qui porterait  et
et  sur ses axes horizontaux et verticaux.
sur ses axes horizontaux et verticaux.
Ensuite celui devant dont le dénominateur peut valoir 0 pour une certaine valeur de x_1. Plus précisément, il y a divergence de ce coefficient si :
dont le dénominateur peut valoir 0 pour une certaine valeur de x_1. Plus précisément, il y a divergence de ce coefficient si :

Ce qui peut se reformuler en :

La situation de la divergence dépend donc du choix des constantes d'intégration et
et  .
.
Karl est parti avec l'a priori d'un point masse pour étudier la géométrie de l'espace-temps autour. Il a donc choisi une carte en coordonnées cartésiennes dont le centre, qui est sensé être le point masse, est manquant. Avec ces a priori là, il est légitime de choisir car la divergence se retrouve en
car la divergence se retrouve en  , donc
, donc  , donc
, donc  , c'est à dire au centre. En effet, on ne veut pas de divergence ailleurs dans la carte (cas où
, c'est à dire au centre. En effet, on ne veut pas de divergence ailleurs dans la carte (cas où  ), sinon c'est qu'il se passe quelque chose de "bizarre" pour une certaine valeur de r (singularité de coordonnée) et quelque chose d'encore plus bizarre en dessous de cette valeur (la coordonnée t n'est plus temporelle et la coordonnée
), sinon c'est qu'il se passe quelque chose de "bizarre" pour une certaine valeur de r (singularité de coordonnée) et quelque chose d'encore plus bizarre en dessous de cette valeur (la coordonnée t n'est plus temporelle et la coordonnée  n'est plus spatiale car les signes des coefficients de
n'est plus spatiale car les signes des coefficients de  et
et  changent).
changent).
Légitime, mais pas forcément nécessaire, surtout si on se défait des a priori. Et d'ailleurs, pourquoi pas même , comme ça il n'y a aucune divergence nulle part.
, comme ça il n'y a aucune divergence nulle part.
On est donc arrivé au point crucial, et là il y a quelques petits calculs à faire par ci par là pour voir ce que ça change physiquement de choisir une valeur ou une autre pour . Il faut que j'essaie des choses au brouillon, mais j'intuite qu'on va toucher à quelque chose de très intéressant.
. Il faut que j'essaie des choses au brouillon, mais j'intuite qu'on va toucher à quelque chose de très intéressant.
A plus tard...
m@ch3Never feed the troll after midnight!
- 29/10/2021, 16h27 #85mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
C'est même encore plus direct que je ne le pensait. Fixer la valeur deOn est donc arrivé au point crucial, et là il y a quelques petits calculs à faire par ci par là pour voir ce que ça change physiquement de choisir une valeur ou une autre pour . Il faut que j'essaie des choses au brouillon, mais j'intuite qu'on va toucher à quelque chose de très intéressant.
. Il faut que j'essaie des choses au brouillon, mais j'intuite qu'on va toucher à quelque chose de très intéressant. n'est même pas utile physiquement. Si je pose :
n'est même pas utile physiquement. Si je pose :

et que je remplace dans l'expression de la métrique, j'ai :

de plus si , alors
, alors  , ou encore
, ou encore  ce qui donne :
ce qui donne :

enfin, si je remplace ,
,  et
et  par leurs expressions en
par leurs expressions en  et
et  , j'obtiens :
, j'obtiens :

expression bien reconnaissable, A (notation choisie à dessein ) n'étant autre que le rayon aréal !
) n'étant autre que le rayon aréal !
et tout cela sans fixer !
!
A quoi sert ? il ne sert qu'à dimensionner, dans la carte, la taille de la sphère sur laquelle la singularité de coordonnée survient. Si on veut qu'elle se réduise à un point comme Karl, on choisi
? il ne sert qu'à dimensionner, dans la carte, la taille de la sphère sur laquelle la singularité de coordonnée survient. Si on veut qu'elle se réduise à un point comme Karl, on choisi  . Si on veut qu'elle ait le rayon correspondant à son rayon aréal, on choisi
. Si on veut qu'elle ait le rayon correspondant à son rayon aréal, on choisi  . Mais tout cela n'est qu'une affaire de représentation sur la carte, pas une affaire de physique. Toute la physique qu'on peut prédire dans la géométrie de Schwarzschild se trouve dans cette expression finale, et cette expression finale ne dépend pas de
. Mais tout cela n'est qu'une affaire de représentation sur la carte, pas une affaire de physique. Toute la physique qu'on peut prédire dans la géométrie de Schwarzschild se trouve dans cette expression finale, et cette expression finale ne dépend pas de  , elle dépend de A, et A à un sens physique précis et concret.
, elle dépend de A, et A à un sens physique précis et concret.
Par exemple, si je veux connaitre le périmètre physique d'un équateur arbitrairement proche de la singularité de coordonnée, le périmètre que mesurerait des arpenteurs, je trouverais une valeur arbitrairement proche de , jamais en-dessous et cela quelque soit
, jamais en-dessous et cela quelque soit  . C'est à dire que si on choisi
. C'est à dire que si on choisi  comme Karl, et qu'on s'intéresse au périmètre physique d'un cercle centré sur l'origine, ce périmètre physique tend vers
comme Karl, et qu'on s'intéresse au périmètre physique d'un cercle centré sur l'origine, ce périmètre physique tend vers  quand r tend vers 0. Physiquement, le point masse ne peut pas être un point, c'est forcément une sphère de rayon
quand r tend vers 0. Physiquement, le point masse ne peut pas être un point, c'est forcément une sphère de rayon  .
.
Maintenant qu'on en est arrivé là, il me reste à commenter le message 81. Ces 4 messages d'affilée font un peu flood, désolé. Je verrais pour les fusionner peut-être.
m@ch3Never feed the troll after midnight!
- 29/10/2021, 17h30 #86Mailou75
- Date d'inscription
- novembre 2010
- Messages
- 5 602
Re : Jamais rien ne tomba dans un trou noir ?
Salut mach3,
Deux mois pour répondre c'est pas mal... trahis sans doute une perte d’intérêt pour le sujet.
Rien n'indique qu'elle est valide partout :
- En cosmo (expansion) il manque des cases, trop pour qu'une autre théorie ne la supplante pas
- An astro (galaxies) il en manque aussi, et Newton flipperait s'il savait qu'on se sert de sa formule pour traiter les galaxies
- Aux fortes densités, on peut toujours ignorer la MQ mais bon...
En fait il semblerait qu'elle soit loin de tout expliquer et qu'on vient de passer un siècle à découvrir tous les domaines où elle ne marche pas.
On peut encore en passer un autre à l'aise, vu comme c'est parti... car elle continue de faire loi et d'être la base d'autre lois. Vertigineuse abysse.
Et même Schw, avec tout le respect que je lui dois, ça ne marche pas avec plus d'une dimension* (Pour ça que Kruskal, Penrose et compagnie s'en sortent bien)
* Jusqu'à preuve du contraire mais je ne l'attends plus
Au fond je pense qu'on a pas tout bien compris au sens de la 4D (je pense aux coordonnées de Schw et l'espace des immobiles ou à l'Espace en expansion de la cosmo). L'espace "euclidien virtuel" ce n'est rien d'autre que les 3 dimensions restantes, perpendiculaires à une ligne d'univers, la seule à avoir un sens physique. Les modèles bien confortables pour nos esprits nous éloignent de la compréhension.
Ce qui me chagrine c'est qu'on retrouve la notion de "point culminant" dans ton discours même quand tu ne parles que des régions I et II. Pour culminer il faut bien une origine, une symétrie de la trajectoire, réversible dans le temps. Je ne vois même pas comment la région II peut exister sans la IV, après avoir longtemps milité contre...C'est beaucoup moins évident et beaucoup plus spéculatif pour de la région IV ou pour un pont de Rosen...
Quant aux graphiques d’effondrement en Penrose, peuvent ils faire s'effondrer autre chose qu'un fil (1D) ça c'est la question lol.
Dommage que l'on ai pas pu explorer plus avant LTB, on en aurait sans doute appris un peu plus sur la "réalité" qu'avec Schw.
Inutile de perdre ton temps à me répondre, poursuis plutôt ta démonstration. J'y comprends rien mais je la lis quand même
A+
MailouTrollus vulgaris
- 29/10/2021, 20h07 #87bernarddo
- Date d'inscription
- septembre 2013
- Messages
- 195
Re : Jamais rien ne tomba dans un trou noir ?
Rebonjour,
Voici une réponse rapide, qui sera tout d’abord laudative.
En effet, l’ensemble des 4 posts précédents donne une vision complète et explicative du calcul de Schwarzschild, et qui le valide mathématiquement, ce qui me remplit encore plus d’admiration pour lui, maintenant que vous avez exposé toutes les finesses de son calcul, à moi, simple utilisateur, même averti, des mathématiques de l’ingénieur, qui n’en avais même pas saisi toutes les arcanes. C'est, pour sa part développante, un réel apport à la cosmologie.
C'est sur le dernier post qu'on trouve les 2 gros problèmes:
1 Le premier est la constatation d'une curieuse absence: aucun commentaire fonctionnel n'est fait sur la justification de l'exigence de continuité qui fait la singularité de calcul de Karl. Pour une querelle tournant autour de la validité physique de la solution, il me semble anormal de ne faire aucune évaluation de ce pilier (quoique passé sous silence dans sa démonstration, tant il s'impose physiquement), de l'argumentaire de Karl
2 Le second est plus factuel et mathématique: après avoir repéré le point crucial comme purement opératoire, la fixation d'une valeur de constante d'intégration, il me semble avoir repéré un tour de bonneteau dans le calcul ayant permis de trouver la métrique standard sans avoir à la fixer.
En effet, il ne vous a pas échappé que la constante "rho" fixée par Karl, n'était pas une constante au sens arithmétique.
Ce qui rend fautive l’expression de dA !
Et ruine raisonnement qui suit :
Ce second problème implique que:
A quoi sert ? il ne sert qu'à dimensionner, dans la carte, la taille de la sphère sur laquelle la singularité de coordonnée survient. Si on veut qu'elle se réduise à un point comme Karl, on choisi . Si on veut qu'elle ait le rayon correspondant à son rayon aréal, on choisi . Mais tout cela n'est qu'une affaire de représentation sur la carte, pas une affaire de physique.
m@ch3
- si l'erreur est avérée, l'avantage décisif est à Schwarzschild,
-si elle n'existait pas, il serait au moins nécessaire de démontrer que ce qui aurait constitué un choix arbitraire dans le calcul de Karl, jugé irréprochable, ne serait pas tout aussi arbitraire dans un calcul d'Hilbert, sachant que ce calcul implique forcément la fixation de deux constantes d'intégration.
Plus globalement:
Contrairement à ce qui est affirmé au premier des 4 posts. Karl ne veut pas réduire « la sphère » à un point, il veut simplement se placer sur l’espace-temps réel, celui qui n’a aucune rupture de continuité, et trouver une métrique décrivant sa topologie, ce qui supprime la nécesité de passer par la notion de carte.
Au pire, comme il sait que son cas de figure diffère localement de l’ET physique puisque, en 1916 (et c’est encore le cas aujourd’hui), on ne connaît rien de densité infinie, dans sa volonté de respecter la continuité spatiale (et temporelle), il s’attend à rencontrer, et il est prêt à accepter une solution mathématique présentant une discontinuité pour la situer à ce point physiquement indéfini (et seulement à ce point), ... en plus des deux divergences pathologiques connues, dont il ne fait évidemment pas état dans un papier entre pairs du plus haut niveau.
Ayant pu réaliser tout cela, il en déduit qu’il a donc trouvé ce qu’il cherchait, une métrique valable pour un espace-temps continu, comme le nôtre, et donc représentative des caractéristiques topologiques de cet espace-temps.
Et, cerise sur le gâteau, et pour faire plaisir à Mailou, le calcul apporte de plus la preuve que la courbure d’espace possède une limite, qui est atteinte dans ce cas, ce qui donne le bord intérieur de la variété (i.e. de l’espace-temps), et limite les caractéristiques physiques de la matière dans le « domaine des fortes compacités ».
C’est la solution de Hilbert, qui est incapable de représenter topologiquement l’espace-temps, et donc est réduite au statut de carte d’un atlas formé avec le diagramme de l’extension de Kruskal (et ses cartes « régionales »). Le gros problème, mathématiquement, c’est que l’extension suppose un ds^2 négatif , donc un déplacement imaginaire, chose qu’il est très courant de réaliser entre les cartes d’un atlas, mais impensable à imaginer dans notre monde réel.
- 30/10/2021, 00h32 #88mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
Vite fait, sauf erreur,En effet, il ne vous a pas échappé que la constante "rho" fixée par Karl, n'était pas une constante au sens arithmétique.
Ce qui rend fautive l’expression de dA ! ne dépend que de
ne dépend que de  (
( c'est
c'est  et G ne dépendant que de r, et comme r ne dépend que de
et G ne dépendant que de r, et comme r ne dépend que de  ...). Vu que l'expression de
...). Vu que l'expression de  est trouvée en résolvant une équation differentielle qui ne fait intervenir que les dérivées partielles premières et secondes de
est trouvée en résolvant une équation differentielle qui ne fait intervenir que les dérivées partielles premières et secondes de  par rapport à
par rapport à  , on ne voit pas trop de quoi
, on ne voit pas trop de quoi  pourrait être une fonction. C'est donc une constante,
pourrait être une fonction. C'est donc une constante,  et l'expression de dA est correcte.
et l'expression de dA est correcte.
m@ch3Never feed the troll after midnight!
- 31/10/2021, 18h58 #89bernarddo
- Date d'inscription
- septembre 2013
- Messages
- 195
Re : Jamais rien ne tomba dans un trou noir ?
Même après avoir écrit à la ligne d’avant ?
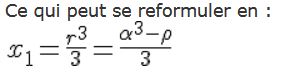

- 31/10/2021, 19h48 #90mach3Modérateur
- Date d'inscription
- mars 2004
- Localisation
- normandie
- Âge
- 43
- Messages
- 14 440
Re : Jamais rien ne tomba dans un trou noir ?
 est l'expression générale de
est l'expression générale de  , même sa définition.
, même sa définition.  est la valeur particulière de
est la valeur particulière de  pour laquelle il y a singularité de coordonnées.
pour laquelle il y a singularité de coordonnées.
m@ch3Never feed the troll after midnight!
« Réflexions sur la géométrie de l'espace-temps
|
Métrique interne de Schwarzschild et équilibre des étoiles à neutrons. »
Discussions similaires
-
Trou noir/trou blanc, rayonnement de Hawking et voyage dans l'espace-temps
Par Jeanveux dans le forum PhysiqueRéponses: 21Dernier message: 26/12/2020, 20h03 -
Mouvement dans un trou noir
Par Nickelange dans le forum Discussions libresRéponses: 39Dernier message: 24/05/2020, 13h40 -
Un trou noir dans le voisinage
Par invite44510b00 dans le forum ActualitésRéponses: 1Dernier message: 07/05/2020, 12h04 -
Compression dans un trou noir
Par invite6c51b64f dans le forum Questions de base et pédagogieRéponses: 6Dernier message: 02/02/2020, 16h14
Fuseau horaire GMT +1. Il est actuellement 17h55.

