C'est vrai...
Alors en toute rigueur, une métrique, cela permet de décrire la géométrie de l'ET...et y poser plein de trucs...1 Il n'y a pas de géométrie de Schwarzschild, mais une métrique qui permet de décrire l'espace-temps
Un petit cours très élémentaire: http://mespages.univ-brest.fr/~scott..._lecture_6.pdf
Vous auriez eu de la curiosité, vous auriez trouvé en qq sec plusieurs cours traitant de ça...
Quand à la logique, il me semble que vous abordez des choses pour lesquelles vous n'êtes pas suffisamment formé (cela se voit à vos questions, et la façon dont vous les posées, ainsi que leurs pertinence), donc revenez en arrière, c'est ce qu'il y a de plus logique à faire.
Pour ma part, je ne pense pas qu'un forum soit fait pour prendre un cours complet, donc je m'arrête là avec vous.
Bonne continuation.
-----




 par la notation
par la notation 
 ), ce n'est pas de la physique, ce sont des maths.
), ce n'est pas de la physique, ce sont des maths.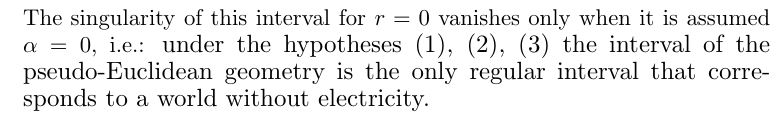
 et mach3 recadrera ce qu'il est nécessaire si il le veut.
et mach3 recadrera ce qu'il est nécessaire si il le veut.