Réflexions sur la géométrie de l'espace-temps (réponse)

[Mailou75]

Salut,

Je rouvre un sujet car l'autre a été fermé trop rapidement :

Je suggère de calculer les choses suivantes dans ce formalisme "alternatif" :
-l'allongement de la durée de vie des muons, soit après création dans la haute atmosphère, soit dans un anneau de stockage comme on peut en trouver au cern
-l'évaluation de la durée écoulée pour le jumeau voyageur de Langevin (un aller-retour), en considérant des accélérations instantanées puis des accélérations realistes
-l'allongement de la ficelle de Bell (tendue entre deux fusée à la queue leu leu qui effectuent la même accélération), vu depuis l'une ou l'autre fusée
-les energies et impulsions de deux photons créés suite à l'annihilation d'un electron et d'un positron en fonction de leurs vitesses

L'hyperbole est à la droite ce que la droite est au cercle

Voilà le seul indice qui rend toutes vos questions inutiles : ce n'est qu'un autre repère en RR !
Pour autant que je sache on ne redémontre pas la RG à chaque fois qu'on change de système de coordonnées (Kruskal, Penrose, Schw, Painlevé...).

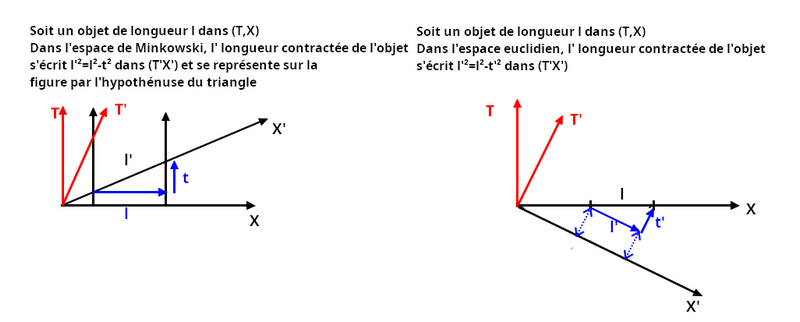
Je pense intimement (mais c'est dur à prouver) que ce système est plus proche de la "réalité" que ne l'est celui de Minkowski. Ce dernier a l'avantage l'avoir un espace et un temps orthogonaux et d'être confortable pour nos esprits simples (Newtonnien en somme). Mais si la RR nous enseigne que l'espace ça n'existe pas, on le voit pourtant réapparaître (partiellement) chez Schw sous la forme de l'espace euclidien des immobiles et (totalement) en cosmo au point qu'on lui confère même des propriétés "élastiques". Hors sujet mais tout de même... se demander ce qu'est l'Espace est une bonne question.

Donc, si ces systèmes sont équivalents il n'en reste pas moins que le second, que je nomme Trigo, est bien moins aisé à lire :
- La compression des objets en mouvement ne peut se lire que de façon infinitésimale
- Il n'y a pas de formule directe (liée à ce sytème) pour trouver le Doppler (cad pas d'équivalent z+1=exp(rapidité)) mais les valeurs restent "lisibles"
- L’aller retour des jumeaux c'est une vraie tanée... je pourrais vous le montrer mais ça ne vous convaincrait pas. Et il ne marche que pour deux particules, on ne pourra pas faire entrer une troisième dans le même schéma, il ne gère que des relations "binaires".

Mais sur le fond, inutile de demander des résultats, ce sont les mêmes que la RR de Minko !

Ce n'est pas toi qui fixe les règles sur Futura

"Discussion libre" pour parler d'un système de coordonnées équivalent à Minko, tout à fait juste, je ne pense pas qu'on soit hors des clous.

Tu bottes en touche

Non, vous bottez en touche car vous ne vous donnez pas la peine de comprendre.
Je ne vous jette pas la pierre... mais ça ne vous autorise pas pour autant à fermer le fil en faisant passer Externo pour un illuminé.

En fait je me sens obligé de le défendre, au moins parce qu'il a partiellement raison. Et si un jour vous comprenez la moitié qui est juste vous pourrez le reprendre sur la moitié fausse.
Ce n'est pas le cas pour l'instant.

Bref, je pourrais vous link une millième fois les schémas montrant l'équivalence Minko-Trigo mais pour ma part j'ai jeté le tablier. Si vous aviez du vous y intéresser ce serait déjà fait...

Bonne journée, a+

Mailou
-----

[mach3]

Voilà le seul indice qui rend toutes vos questions inutiles : ce n'est qu'un autre repère en RR !
Pour autant que je sache on ne redémontre pas la RG à chaque fois qu'on change de système de coordonnées (Kruskal, Penrose, Schw, Painlevé...).

oui, sauf qu'avec le système de coordonnées proposé, on n'obtient pas dt²+dx²+dy²+dz² en changeant de coordonnées, mais tout autre chose...

Donc, si ces systèmes sont équivalents il n'en reste pas moins que le second, que je nomme Trigo, est bien moins aisé à lire :
[...]
Mais sur le fond, inutile de demander des résultats, ce sont les mêmes que la RR de Minko !

ce qui confirme le fond de ma pensée : à quoi bon si c'est plus compliqué ? on peut aussi travailler sans coordonnées du tout, pour la beauté de la chose (d'ailleurs cela reste faisable pour les 4 exemples que j'ai proposé), mais d'une manière générale, c'est juste se compliquer la vie.

Pour le reste on est à la limite de la critique de la modération (sans compter le contournement d'une décision de modération que ce fil peut représenter), faudra pas s'étonner si une sanction tombe.

m@ch3

[externo]

Je vais essayer de répondre aux deux premiers points (muons et jumeaux) quand j'aurai le temps si le fil reste ouvert.
Mais il est entendu que ce n'est qu'un formalisme mathématique, un simple exercice, et que ça n'a rien à voir avec remettre en cause quoi que ce soit.

La compression des objets en mouvement ne peut se lire que de façon infinitésimale

Voilà un truc que je ne comprends pas. Il y a une différence entre l'approche de Mailou et la mienne. Je ne vois rien d'infinitésimal de mon côté.

[Mailou75]

Salut,

Voilà un truc que je ne comprends pas. Il y a une différence entre l'approche de Mailou et la mienne. Je ne vois rien d'infinitésimal de mon côté.

C’est parce que tu ne t’intéresses qu’à ce qui «est» (cad le rapport des choses qui est purement mathématique) et pas à ce qui est «vu» qui doit nécessairement être juste graphiquement (et donner le même résultat que Minkowski, forcément) : un rayon lumineux va croiser l’avant et l’arrière d’un objet pour pouvoir définir une longueur vue, ce sont deux événements que tu ne peux pas représenter avec ta méthode qui se limite aux rapports. Il n’y a d’ailleurs pas de rayons lumineux dans tes figures, ce qui pose forcément problème.

Si j’ai le temps un des ces jours je mettrai ça au propre qu’on arrête de tergiverser.
En ce moment c’est compliqué avec le taf mais j’essayerai, promis.

Mailou

[A voir en vidéo sur Futura]

[Mailou75]

Re,

oui, sauf qu'avec le système de coordonnées proposé, on n'obtient pas dt²+dx²+dy²+dz² en changeant de coordonnées, mais tout autre chose...

Ah ça j'en sais rien, tu sais les métriques c'est pas mon truc...

ce qui confirme le fond de ma pensée : à quoi bon si c'est plus compliqué ?

Minkowski doit se "tordre" et suivre des hyperboles pour conserver un temps et un espace orthogonaux. C'est une étape sans doute nécessaire pour appréhender des résultats, mais peut être pas pour comprendre le fond du problème. La version Trigo, malgré ses handicaps, montre aisément pourquoi "la norme du quadrivecteur vaut 1". Elle est géométriquement plus élégante à mon goût et c'est cette géométrie qui me fait penser que cette représentation est plus proche du "réel". Enfin elle montre naturellement le rapport entre vitesse et facteur de Lorentz qui sont les sin et cos d'un même angle trigo. Je suis désolé mais à part le coté "pratique" de Minko, rien n'aide à comprendre les "pourquoi" qui trouvent des réponses évidentes en Trigo.

Pour le reste on est à la limite de la critique de la modération

Je critiquais la fermeture, oui. Et peut être le manque d'ouverture

Bonne nuit

[Deedee81]

Salut,

Mais il est entendu que ce n'est qu'un formalisme mathématique, un simple exercice, et que ça n'a rien à voir avec remettre en cause quoi que ce soit.

Vu comme ça, no stress (c'est pas ça qui m'avait gonflé comme aurait Vahiné). Ca peut être intéressant.

Je critiquais la fermeture, oui. Et peut être le manque d'ouverture

Comme disait Obi, faut quand même éviter la fracture du crâne
Et sans rire : l'ouverture d'esprit se pratique largement en science mais pas sur Futura où on ne fait pas de science. On en parle. Ce qui n'est pas vraiment la même chose.

Ce qui serait intéressant est d'avoir un développement formel rigoureux (a supposer que ce soit possible (*)). Pas les graphiques qui sont presque toujours imbuvables. Le "visuel" n'est pas toujours pédagogique.

(*) Comme pointé par March3. Les variétés décrites par des métriques de signature différentes sont des variétés différentes. Et un changement de coordonnées ne change pas la variété. Donc je doute qu'on puisse obtenir quelque chose de valable. Mais rien n'empêche d'essayer (si il y a un peu plus qu'un changement de coordonnées, qui sait) ..... qui que ce soit qui en a le courage (et le temps). Juste une requête pour éviter le vert, s'il vous plaît, ne transformez pas la discussions en "blog de recherche". Pondez ça à part, off line, dans une document. Avec tout le détail et tout. Puis vous le copier ici (ou si trop long, un lien sur une archive quelconque.... pas sur le C:\ évidemment )

[Matmat]

Minkowski doit se "tordre" et suivre des hyperboles pour conserver un temps et un espace orthogonaux. C'est une étape sans doute nécessaire pour appréhender des résultats, mais peut être pas pour comprendre le fond du problème. La version Trigo, malgré ses handicaps, montre aisément pourquoi "la norme du quadrivecteur vaut 1". Elle est géométriquement plus élégante à mon goût et c'est cette géométrie qui me fait penser que cette représentation est plus proche du "réel". Enfin elle montre naturellement le rapport entre vitesse et facteur de Lorentz qui sont les sin et cos d'un même angle trigo. Je suis désolé mais à part le coté "pratique" de Minko, rien n'aide à comprendre les "pourquoi" qui trouvent des réponses évidentes en Trigo.

Bonjour,
Certaines représentations éloignent de la RG . C'est le danger : s'habituer à comprendre les choses de façon trigo n'aide pas à progresser vers la RG.
La raison pour laquelle la norme du quadrivecteur vitesse vaut 1 est dans la géométrie différentielle quand on reparamétre un arc par l'abscisse curviligne (où, comme conséquence à ce reparamétrage, la norme de dérivé du vecteur tangeant parcourant l'arc vaut 1).

[Deedee81]

Attention, généraliser et voir l'utilité en RG est utile (sinon je suis d'accord, la vue la plus profonde de la RG est la géométrie différentielle, pas l'approche composante ou l'approche trigo)

Mais la question initiale est en RR. Essayons de ne pas tout compliquer Ce que je proposais ci-dessus, c'est sur la formulation mathématique alternative avec la proposition d'externo et en RR.

[ordage]

Mais il est entendu que ce n'est qu'un formalisme mathématique, un simple exercice, et que ça n'a rien à voir avec remettre en cause quoi que ce soit.

Bonjour
Une remarque d'ordre général.
Dans des coordonnées t, x, y, z sur une base orthonormée de 4 vecteurs.

ds² = dt² + dx²+dy²+dz² (1)

est la métrique d'un espace euclidien à 4 dimensions, dont toutes les dimensions repérées par les coordonnées t, x, y, z sont de type espace (elles contribuent de la même manière au ds², et ce n'est pas parce qu'on en appelle une t que cela lui confère un caractère temporel: l'habit ne fait pas le moine!).
Ainsi dx/dt n'est pas une vitesse mais un rapport de 2 longueurs c.a.d un nombre.
Pour décrire la mécanique la RR propose un espace-temps qui remplace le temps absolu et l'espace absolu de la mécanique newtonienne.

Ainsi, dans la métrique de Minkowski:
ds² = -dt² +dx²+dy²+dz² (2)

La coordonnée t contribue ne manière opposée à x, y, z ce qui montre que t et (x,y,z) ne sont pas de même type. C'est le signe "-" qui précède dt qui caractérise son caractère temporel, pas son libellé.
A noter que (1) se ramène à (2) si on pose T = i.t. (rotation de Wick).
Un exemple avec le paradoxe de Langevin traité en géométrie euclidienne puis transformé géométrie minkowskienne en:
http://www-cosmosaf.iap.fr/Langevin-Wick.pdf
Cordialement

[externo]

Très bien.

Mais l'idée ici est de prendre l'égalité invariante -dt² +dx²+dy²+dz² = -dt'² +dx'²+dy'²+dz'² et de la réécrire comme dt'² +dx²+dy²+dz² = dt² +dx'²+dy'²+dz'² et d'étudier les phénomènes de relativité dans cet espace euclidien là, car c'est plus palpable aux sens. C'est comparable au diagramme de Loedel.

[externo]

Et j'ajoute que ça revient aussi à passer de la métrique dtau² = dt²-dx²-dy²-dz² à la métrique dt² = dtau² +dx²+dy²+dz²

[Mailou75]

Un exemple avec le paradoxe de Langevin traité en géométrie euclidienne puis transformé géométrie minkowskienne en:
http://www-cosmosaf.iap.fr/Langevin-Wick.pdf

Sérieux ?

Un dessin 2D avec des formules 2D du genre a=v²/R, une vitesse constante, un témoin (A-E) mobile, on écrit "t" discrètement sur un axe... WTF ?
Ensuite on fixe l'angle A=a.t... le premier qui me sort une application numérique avec un angle en m/s je lui envoie un chèque de 100 balles par la poste ! Le graphe est intraçable.
"A" n'est autre que N=a.t/c c'est à dire la rapidité de la RR déguisée qui permet, avec la bidouille de i qui transforme les fonctions trigo en fonctions hyperboliques, de retrouver Rindler. Bravo.
Pour ma part : arnaque mathématique sans intérêt.

On parle d'autre chose avec Externo. Et même pas dit qu'on parle tous les deux de la même chose

A +

Edit PS : Je suis curieux de savoir quelle vitesse peut atteindre Wick si on le laisse tourner sur lui même suffisamment longtemps ? Mouahaha

[Mailou75]

Salut,

C'est le danger : s'habituer à comprendre les choses de façon trigo n'aide pas à progresser vers la RG.

Je ne crois pas que tu saches de quoi je parle, quiproquo.
Je n'ai jamais dit c'était plus facile à interpréter, au contraire. Mais peut être que ça explique le "pourquoi", là où Minko se limite à "combien".
Et il existe un système Trigo aussi pour Schwarzschild, pour Rindler aussi, c'est juste un changement de coordonnées, c'est pourquoi je ne comprends pas vos réactions.
Autant pour Schw on avait pléthore de systèmes, autant en RR Minko se sent un peu seul. C'est simplement une autre lecture de la même chose !

quand on reparamétre un arc par l'abscisse curviligne (où, comme conséquence à ce reparamétrage, la norme de dérivé du vecteur tangeant parcourant l'arc vaut 1

Rien compris... mais c'était sympa quand même

A+

[ordage]

Pour ma part : arnaque mathématique sans intérêt.

Bonjour
Arnaque largement utilisée par S. Hawking dans son modèle de l 'univers sans borne...
https://www.youtube.com/watch?v=GegAvpiWd_Q
Cordialement

[externo]

J'ai l'impression qu'il y a un lien entre les coordonnées de Rindler et de Painlevé. Dans ces systèmes on prend le point de vue de la ligne d'univers de l'objet en mouvement. Me reprendre si je me trompe.
Mais cela ne change pas l'espace-temps en soi. La métrique de l'espace-temps est toujours celle de Minkowski d'un côté et celle de Schwarzschild de l'autre.
Alors qu'en remplaçant "minko" par "trigo" c'est l'espace-temps lui-même qui est défini différemment.
D'ailleurs, j'ai fait le diagramme des jumeaux en euclidien, avec les calculs associés. La figure marche bien dans le référentiel immobile, mais je n'arrive pas à passer dans le référentiel en mouvement et à conserver la cohérence. J'ai l'impression que je me heurte à ce problème parce que la seule métrique homogène est celle de Minkowski.

[externo]

La difficulté de la représentation de Minkowski c'est que les calculs ne correspondent pas avec l'image. La représentation de Loedel permet de les faire correspondre.
Il en est question dans wikipedia
https://fr.wikipedia.org/wiki/Diagramme_de_Minkowski, mais en se focalisant sur l'axe du temps.
Sur l'axe d'espace ça donne ça :

[externo]

Dans mes réflexions pour me figurer la géométrie de l'espace-temps je viens de comprendre quelque chose que je n'avais (je cois) encore jamais remarqué :
Vous êtes dans une fusée qui se déplace à vitesse constante et vous regardez par le hublot des horloges synchronisées entre-elles, alignées dans l'espace extérieur et immobiles.
Bien sûr on suppose que vous voyez ce qui "est" et non pas ce qui est visible. Vous voyez les choses instantanément.
Eh bien les horloges avanceront sous vos "yeux" plus vites que la vôtre dans la fusée.
Le temps semblera accéléré à l'extérieur de la fusée par rapport à votre temps, et non pas ralenti comme on nous le rabâche.
Donc quand vous arrivez à votre destination vous arrivez directement chez des gens qui sont dans votre propre futur et votre jumeau est plus âgé que vous.

Certaines personnes doutent-elles de cela ? Je peux l'expliquer.
Certains peuvent l'expliquer à ma place s'ils sont déjà au courant.

[Mailou75]

Salut Ordage,

Arnaque largement utilisée par S. Hawking dans son modèle de l 'univers sans borne...
https://www.youtube.com/watch?v=GegAvpiWd_Q

J'ai essayé de me renseigner sur cet univers sans borne de Hawking, que je ne connaissais pas, et je n'ai pas trouvé grand chose de clair...
La vidéo de ton lien parle essentiellement de i, accessoirement t=iT. Si c'est indispensable pour que la "métrique" fonctionne pourquoi pas, perso je m'intéresse aux schémas, au résultat.
Au moins j'aurais compris ce qu'est la rotation de Wick, merci.

Il n'en reste pas loin que le schéma 2D des jumeaux c'est n'importe quoi. Pour me faire changer d'avis il faudra me dire ce qu'est un angle en m/s.

t, x, y, z sont de type espace (elles contribuent de la même manière au ds², et ce n'est pas parce qu'on en appelle une t que cela lui confère un caractère temporel: l'habit ne fait pas le moine!)

Et j'aimerais revenir là dessus. En fait si, l'habit fait le moine : dans la version Trigo, telle que je la conçois, c'est le choix de la ligne d'univers qui définit l'axe de temps du repère. Trivial. Il n'y a pas de "ségrégation" comme chez Minko : au dessus de 45° genre temps et en dessous genre espace. Toutes les directions peuvent être de genre temps. La perpendiculaire n'est l'espace que localement, sinon c'est une autre ligne d'univers, en mouvement relatif. Bref quand on s'y intéresse, même si c'est pas facile à lire pour notre cerveau, il y a deux ou trois choses évidentes.

Je pense que ce dont on parle n'est ni la rotation de Wick, ni l’univers de Hawking.

[Mailou75]

Salut Externo,

Par rapport à tes schémas, deux ou trois choses...

Minkowski :
Ok pour la représentation et ok pour le calcul. Mais il faut comprendre que le L' du calcul est l'intervalle d'espace temps, invariant quel que soit le repère. C'est la distance 4D entre deux évènements : les extrémités du segment L'. Il se trouve que c'est aussi, dans un repère (T';X') un intervalle sur l'axe d'espace, une distance. C'est en changeant de repère et en prenant le point de vue de monsieur prime que tu verras graphiquement pourquoi L' est plus court que L. Et c'est ça qu'on appelle la compression des longueurs, ton texte est donc inadéquat.

Trigo :
Tu joues sur les rapports, ce n'est pas un système. D'ailleurs où est passée l'autre trajectoire, une ligne a disparu entre les deux schémas, car tu ne sais pas où la mettre... sauf de manière infinitésimale en donnant une "épaisseur" aux axes T, cad aux lignes d'univers. Je me souviens avoir essayé et je crois bien que ça marchait, faudrait que je revérifie. Peu importe, ce repère ne sert pas à ça a priori...

Tu devrais compléter ton Minkowski et ajouter des rayon lumineux. Il sert aussi/surtout à ça !

Eh bien les horloges avanceront sous vos "yeux" plus vites que la vôtre dans la fusée.

Oui ça s’appelle l'Effet Doppler mais ça dépend où tu regardes, vers l'arrière ce sera ralenti. Accéléré = blueshift ; Ralenti = redshift

A+

[mach3]

EDIT : réponse à Externo, croisement avec mailou que je n'ai pas lu

Attention à ne pas faire une confusion (il n'y en peut-être pas, c'est juste au cas où).

Replaçons bien les choses de façon rigoureuse pour être sûrs de parler de la même chose :
On considère des horloges synchronisées (façon Einstein-Poincaré) et immobiles par rapport à un référentiel galiléen R. Elles sont disposées suivant une ligne droite.
On considère un observateur en mouvement rectiligne uniforme par rapport à ce référentiel R, son mouvement suivant la ligne droite le long de laquelle les horloges sont disposées. Quand il passe devant la première horloge, il remet sa montre à l'heure pour qu'elle indique la même chose que cette horloge. Ensuite, à chaque fois qu'il passe devant une des horloges, il regarde l'heure qu'elle indique et compare à sa montre.
La relativité restreinte prédit alors que croisement d'horloge après croisement d'horloge, l'heure indiquée par les horloges successive avance de plus en plus par rapport à sa montre.
Attention cependant. Cela ne veut pas dire que ces horloges "tournent plus vite" que sa montre. D'ailleurs au moment où il passe juste devant, il constate sans ambiguïté que chaque horloge "tourne moins vite" que sa montre (effet Doppler transverse). C'est juste que ces horloges ne sont pas synchronisées pour cet observateur. Dans la datation de son référentiel R', ces horloges, synchronisées pour R, avancent d'autant plus qu'elles sont loin sur la ligne droite : l'opération de synchronisation apparaît avoir échoué. En fait elle ne fonctionne que pour les observateurs immobiles par rapport à R.

m@ch3

[Mailou75]

On a pas eu la même interprétation ^^

[externo]

@mach3
Oui c'est ça, mais je ne fais pas intervenir l'effet Doppler (avec lequel j'ai du mal). A ma façon de voir, la désynchronisation des horloges résulte de l'accélération initiale. Je dis bien que je ne raisonne pas sur ce que l'on "voit" mais sur ce qui "est"

@mailou
J'ai pas tout compris, il me faut réfléchir.

[externo]

Il me semble que l'effet Doppler c'est :
Au voyage d'aller les deux jumeaux reçoivent les signaux lumineux au ralenti, puis après le demi tour le jumeau qui revient reçoit en accéléré jusqu'au retour, alors que le jumeau sur terre ne reçoit les signaux en accéléré qu'après un certain temps.

Mais dans la vue "existentielle", ce qui se passe, c'est que le temps du jumeau dans l'espace est plus lent que celui resté sur terre durant tout le voyage. Par contre, pour le jumeau parti, du fait de la désynchronisation des horloges, par rapport à lui, le jumeau resté sur terre va se retrouver fortement ralenti dans le temps voire aller à reculons. Si on suppose l'accélération instantanée le jumeau sur terre passe instantanément du présent au passé. Pendant la phase à vitesse constante, les deux vont vieillir chacun moins que l'autre. Au moment où le jumeau s'arrête, le jumeau sur terre se retrouve d'un coup plus vieux que le jumeau parti, en fait il a vieilli autant que la destination de la fusée. Maintenant que le jumeau s'est arrêté, tout le monde est synchronisé et l'heure marquée sur terre est la même que celle de la destination. Le jumeau fait demi tour et accélère et le jumeau sur terre part illico dans son futur, vieillissant encore davantage, pendant le trajet à vitesse constante les deux vont vieillir chacun moins que l'autre, et au retour l'écart d'âge entre les deux jumeaux sera deux fois plus important qu'au moment de la pause à la destination, mais moins important que juste après l'accélération. Le ralentissement final va resynchroniser la destination, qui avait reculée dans le temps à son tour si on suppose l'accélération instantanée, et elle marquera désormais la même heure que la terre.

[Mailou75]

Il me semble que l'effet Doppler c'est :
Au voyage d'aller les deux jumeaux reçoivent les signaux lumineux au ralenti, puis après le demi tour le jumeau qui revient reçoit en accéléré jusqu'au retour, alors que le jumeau sur terre ne reçoit les signaux en accéléré qu'après un certain temps.

Oui, c'est à peu près ça.

Pour le reste c'est du grand n'importe quoi. Il pourrait y avoir une interprétation des "il part illico dans son futur" avec les changement de datation lors du demi tour mais c'est risqué...

J'avais tenté un petit recap des Jumeaux ici https://forums.futura-sciences.com/p...ml#post6759459
Ca devrait te permettre de comprendre le Doppler et les changements de repère.

Bonne nuit

[externo]

Lors de l'accélération, la ligne de simultanéité change pour celui qui accélère, c'est à ce moment que l'espace se compresse. Et tu peux te le figurer dans un triangle euclidien, comme d'habitude.
La distance comprimée vers ma destination²+ la différence de temps entre moi et ma destination² = la distance propre à ma destination²
Dans mes dessins plus haut, le dessin de droite, imagine que l c'est la distance à parcourir, alors dans le repère prime cette distance est vue comprimée en l' et par compensation la destination (l'extrémité du segment) est vue dans un futur t'. C'est comme ça que ça marche, le trajet à effectuer est une distance, comme si c'était une règle, et quand elle se compresse, les horloges ne sont plus synchronisées le long de cette règle et celles situées à la destination marquent une heure positionnée dans le futur.

Si on suppose l'accélération instantanée le jumeau sur terre passe instantanément du présent au passé.

Là je me suis trompé, si l'accélération est instantanée alors la fusée est encore sur terre au moment de l'accélération et la terre ne se désynchronise pas. Ce sont les objets qui se trouvent en arrière du trajet qui basculent dans le passé.

[Lansberg]

Bonjour,

Mais dans la vue "existentielle", ce qui se passe, c'est que le temps du jumeau dans l'espace est plus lent que celui resté sur terre durant tout le voyage.

Piégeux ! L'horloge du voyageur fonctionne exactement de la même manière que celle du Terrien.

[mach3]

Mais l'idée ici est de prendre l'égalité invariante -dt² +dx²+dy²+dz² = -dt'² +dx'²+dy'²+dz'² et de la réécrire comme dt'² +dx²+dy²+dz² = dt² +dx'²+dy'²+dz'² et d'étudier les phénomènes de relativité dans cet espace euclidien là, car c'est plus palpable aux sens. C'est comparable au diagramme de Loedel.

Non, ce n'est pas un espace euclidien, car pour ce faire il faudrait que dt² +dx'²+dy'²+dz'² (ou dt'² +dx²+dy²+dz²) soit une expression de la métrique euclidienne, ce qu'elle n'est pas, vu que ce n'est pas l'expression d'une métrique, mais l'expression d'une forme bilinéaire ad hoc

Et j'ajoute que ça revient aussi à passer de la métrique dtau² = dt²-dx²-dy²-dz² à la métrique dt² = dtau² +dx²+dy²+dz²

idem, dt² = dtau² +dx²+dy²+dz², n'est pas l'expression d'une métrique, et ce n'est même pas une forme bilinéaire ad hoc car tau n'est pas un champ scalaire a priori.

une expression du genre Adm²+Bdn²+Cdp²+Ddq² n'est l'expression d'une métrique que si m, n, p et q répondent à une certaine définition. C'est la résutante de quelque chose de plus général et abstrait, une variété Riemmannienne sur laquelle on a défini des champs scalaires.

Ok pour étudier ce que ça donne ces expressions dans des diagrammes (même si je n'y vois aucun intérêt, et que j'y vois un danger pour la bonne compréhension), mais pas d'accord pour utiliser des termes bien définis à contre-sens.

m@ch3

[mach3]

Non, ce n'est pas un espace euclidien, car pour ce faire il faudrait que dt² +dx'²+dy'²+dz'² (ou dt'² +dx²+dy²+dz²) soit une expression de la métrique euclidienne, ce qu'elle n'est pas, vu que ce n'est pas l'expression d'une métrique, mais l'expression d'une forme bilinéaire ad hoc

Plus précisément, si on a t,x,y,z un système de coordonnées de Lorentz, on peut exprimer la métrique :



J'utilise une notation non simplifiée pour appuyer sur le fait qu'on ne manipule pas des nombres ni même des infinitésimaux, mais des formes bilinéaires.

Si on a et t',x',y',z', un autre système de coordonnées de Lorentz, on a :



Donc :



On retranche et on prend l'opposé :



En repassant en notation "simplifiée", cela donne :



En version non simplifié, la forme bilinéaire n'est pas une métrique, le résultat qu'on obtiendra en lui fournissant deux vecteurs dépendra des deux systèmes de coordonnées t,x,y,z et t',x',y',z' qu'on aura choisi arbitrairement. C'est une forme bilinéaire ad hoc, définie spécifiquement pour le couple de systèmes de coordonnées choisis et qui ne vaut pas pour d'autres.

En version simplifiée, ce "machin", , ne peut pas être qualifié d'invariant car il dépend explicitement de coordonnées choisies arbitrairement.

m@ch3

[externo]

Ok pour étudier ce que ça donne ces expressions dans des diagrammes (même si je n'y vois aucun intérêt, et que j'y vois un danger pour la bonne compréhension)

Ces diagrammes ont un intérêt conceptuel certain.
Si on considère une fusée (longueur l') dans le référentiel (T'X') de la figure de droite, depuis (T,X) on constate non seulement que cette fusée est "vue" compressée mais qu'elle est dirigée vers le passé, cad que les horloges remontent le temps de l'arrière vers l'avant de la fusée.
Si on considère une distance spatiale (longueur l) dans (T,X) on constate non seulement que cette distance est "vue" compressée depuis (T'X') mais qu'elle est dirigée vers le futur cad que les horloges se désynchronisent de plus en plus dans le futur avec l'éloignement.
C'est ce qu'il y a de mieux pour comprendre les conséquences d'une accélération.

[ordage]

Il n'en reste pas loin que le schéma 2D des jumeaux c'est n'importe quoi. Pour me faire changer d'avis il faudra me dire ce qu'est un angle en m/s.

.

Bonjour
J'ai regardé, non c'est correct. Une habitude est que dans les calculs intermédiaires, on s'intéresse surtout aux relations, l'aspect dimensionnel est mis entre parenthèses. On le rétablit en temps utile. Ce qui est fait d'ailleurs, dans le texte, juste après, en donnant l'angle en radians. Mais comme ce n'est pas ta préoccupation, je n'insiste pas.
Cordialement