nombre d'or

[noue]

Bonjour,

J'aimerais savoir ce qu'est le fameux nombre d'or (1+rac5)/2. Pourquoi est-il si célèbre et que permet-il de calculer?
D'après ce que j'ai compris c'est le nombre divin, le nombre de la nature mais c'est très étrange.
merci
-----

[ansset]

bonsoir,
je n'ose te donner un lien, tellement il y a de textes.
il n'a rien d'étrange, c'est une proportion particulière, mais que l'on retrouve dans la "nature".
mais ce(s) fait(s) est(sont) parfaitement explicable(s) ( rien de divin ).

de manière très éloignée, c'est un peu comme si on trouvait le fait que la forme hexagonale des alveoles des ruches était magique.

[Xoxopixo]

Bonjour,

c'est juste que (a+b)/a=a/b
Ce qui amène à une spirale logarithmique particulière, la spirale d'or :

Cette spirale est un cas particulier de spirale logarithmique.
Comme toute spirale de cette famille, elle possède une propriété caractéristique, si A est un point de la spirale, alors la droite passant par le centre de la spirale et A fait un angle constant avec la tangente à la spirale en A.

http://fr.wikipedia.org/wiki/Nombre_d'or

Approximate logarithmic spirals can occur in nature (for example, the arms of spiral galaxies[5] or phyllotaxis of leaves); golden spirals are one special case of these.
It is sometimes stated that spiral galaxies and nautilus shells get wider in the pattern of a golden spiral, and hence are related to both φ and the Fibonacci series.
[6] In truth, spiral galaxies and nautilus shells (and many mollusk shells) exhibit logarithmic spiral growth, but at a variety of angles usually distinctly different from that of the golden spiral.[7][8][9]
This pattern allows the organism to grow without changing shape.

http://en.wikipedia.org/wiki/Golden_spiral

Concernant la spirale logarithmique :

Spira mirabilis, Latin for "miraculous spiral", is another name for the logarithmic spiral. Although this curve had already been named by other mathematicians, the specific name ("miraculous" or "marvelous" spiral) was given to this curve by Jacob Bernoulli, because he was fascinated by one of its unique mathematical properties: the size of the spiral increases but its shape is unaltered with each successive curve, a property known as self-similarity.

Possibly as a result of this unique property, the spira mirabilis has evolved in nature, appearing in certain growing forms such as nautilus shells and sunflower heads.
Jakob Bernoulli wanted such a spiral engraved on his headstone along with the phrase "Eadem mutata resurgo" ("Although changed, I shall arise the same."), but, by error, an Archimedean spiral was placed there instead.[2][3]

http://www.princeton.edu/~achaney/tm...ic_spiral.html

[Fritz.Haber]

Le nombre d'or est aussi le seul entier positif qui, élévé au carré donne le même nombre +1

[A voir en vidéo sur Futura]

[Fritz.Haber]

D'ailleur, si on "découpe" un rectangle d'or en un carré et un rectangle x, le rectangle obtenu (le rectangle x) s'avère être également un rectangle d'or. (voir image ci-dessous)

[Paraboloide_Hyperbolique]

Bonsoir,

Le nombre d'or est aussi le seul entier positif...

Je poste juste ce message histoire signaler une erreur que je ne peux pas laisser passer.
Une petite inattention de votre part ?

[Fritz.Haber]

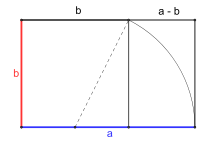
Bien sur, bête erreur de ma part, bien évidement, le nombre d'or est irrationnel, il ne peut pas être entier.
Il faut remplacer Entier par nombre ou Réel, mais je n'arrive plus à modifier.

Merci d'avoir signalé cette faute de distraction.

[noir_ecaille]

Vous pouvez toujours signaler votre propre post à la modération et avec beaucoup de courtoisie expliquer votre problème, ainsi que le signale d'ailleurs le petit message de fin de délai de modification du post.

Cependant, comme le nombre d'or vaut approximativement 1,6180339887, son carré peut difficilement être égal à 1...

[Garion]

En fait, étant mathématiquement un nombre remarquable, il est normal qu'on le rencontre et qu'on le remarque aussi dans la nature (Tout comme Pi d'ailleurs).

[ansset]

Il y a pas mal de vidéos sur le net,mais beaucoup font du prosélitisme religieux ou autre.
cell-ci est plus mignone :
http://www.youtube.com/watch?v=W87EPJ9-zqk

[noir_ecaille]

Sympa cette vidéo ^^ Pour une fois on peut ressentir à quel point les mathématiques peuvent être belles

[polo974]

Oui, enfin, bon, hein, les cagouilles ne respectent pas le nombre d'or de façon très précise, on trouve facilement des espèces qui s'en écarte même beaucoup...

Comme d'hab, quand on cherche un nombre dans la nature, on le trouve un peu partout (à peu près)...

[ansset]

non, ce n'est pas exact, pas dans le sens ou tu le dit.
que veut dire "de façon très précise"? , le monde biologique est "analogique" pas numérique.
et le lien entre les exmples montrés et phi a des explications très rationnelles.
il n'y a rien de magique.
la croissance des fleurs d'une plante vise par exemple à optimiser l'exposition au soleil de chacune.

en résumé, je ne comprend pas ta remarque.
ceci par exemple :
"on trouve facilement des espèces qui s'en écarte même beaucoup...".
je ne comprend pas l'induction logique sensée en découler !

[JPL]

la croissance des fleurs d'une plante vise par exemple à optimiser l'exposition au soleil de chacune.

La croissance des fleurs ne vise à rien.

[noir_ecaille]

Elles ont juste été sélectionnées ainsi au fil des générations

[polo974]

non, ce n'est pas exact, pas dans le sens ou tu le dit.
que veut dire "de façon très précise"? , le monde biologique est "analogique" pas numérique.
...
en résumé, je ne comprend pas ta remarque.
ceci par exemple :
"on trouve facilement des espèces qui s'en écarte même beaucoup...".

Vu qu'on trouve des coquillages qui ont une progression de moins de 1.1 et d'autres qui atteignent 1.8, y rechercher le nombre d'or est facile, si on n'est pas trop regardant...

je ne comprends pas l'induction logique sensée en découler !

ce n'est pas parce qu'on en trouve une (espèce de mollusque) qui colle à peu près qu'il y a une relation.

ensuite, pour la vidéo, au début, on utilise la spirale d'or pour construire un mollusque de synthèse, facile alors de retrouver son copain...
pour la fin de la vidéo, j'aimerais bien qu'on me montre la relation entre le nombre d'or et le maillage hexagonal de l'oeil d'un insecte...

[ansset]

bonjour,
oui, je ne vois aussi aucun lien avec la dernière image ( zoom sur un hexagone ).
pour un pentagone, c'est différent :
http://fr.wikipedia.org/wiki/Nombre_...et_pentagramme
Et j'ai comme l'impression que tu t'adresses à moi comme l'auteur de cette vidéo et de surcroit avec une intention d'interprétation que je n'ai pas.
Tu sur-interprètes mon intervention.
j'ai d'ailleurs dénoncé dans mon premier mess que beaucoup faisait l'amalgame entre ces corrélations qui existent et une inférence "divine".
( beaucoup de video dans ce sens ).
Mais dans l'autre sens, ne voir dans les correlations qui existent que des "coups de bol" , me semble se mettre de la peau de saussisson sur les yeux.
L'exemple du tournesol ( entre autre ) est flagrant ( et à deux titres ).
( je ne reparle pas des pentagones ).

donc, que cette proportion ( qui a des propriétés simples, mais qui peuvent s'averer "efficasses" ) se retrouve dans le monde physique ne me gène pas.
mais que l'on dise :
bof, c'est comme n'importe quel autre nombre, non.

les planêtes sont bien sphérique pour des raisons physiques , ce qui les amènent à avoir des proportions qui font intervenir pi.
celà ne choque personne, me semble-t-il.
et Pi intervient dans de nombreuses equations physiques , ( par uniquement en géométrie )
est-ce divin ? non !

[JPL]

cette proportion ( qui a des propriétés simples, mais qui peuvent s'averer "efficasses" )

Tu as raison de mettre des guillemets. Sans guillemets c'est efficace

[ansset]

sorry !
cordialement.

[polo974]

bonjour,
oui, je ne vois aussi aucun lien avec la dernière image ( zoom sur un hexagone ).
pour un pentagone, c'est différent :
http://fr.wikipedia.org/wiki/Nombre_...et_pentagramme
Et j'ai comme l'impression que tu t'adresses à moi comme l'auteur de cette vidéo et de surcroit avec une intention d'interprétation que je n'ai pas.

Non, je répondais à ta réponse à mon intervention, sans plus.

Tu sur-interprètes mon intervention.
j'ai d'ailleurs dénoncé dans mon premier mess que beaucoup faisait l'amalgame entre ces corrélations qui existent et une inférence "divine".
( beaucoup de video dans ce sens ).

Non, et je vais dans ton sens "anti-déique" (peut-être un peu plus bourrin...).

Mais dans l'autre sens, ne voir dans les correlations qui existent que des "coups de bol" , me semble se mettre de la peau de saussisson sur les yeux.
L'exemple du tournesol ( entre autre ) est flagrant ( et à deux titres ).

C'est vrai que le tournesol est un bel exemple.

et encore, je n'en ai pas un sous le coude pour le décortiquer au centre...
car en gros les angles de la forme (360/(N+phi)) (N étant un nombre entier) donnent une répartition "harmonieuse" (sauf au centre pour les grands N).
donc les angles ((très) arrondis):
137,5
99,5
78,0
64,1
54,4
47,3
41,8
37,4
33,9
31,0
sont dignes de considération, mais il descendent tous de phi...

( je ne reparle pas des pentagones ).

donc, que cette proportion ( qui a des propriétés simples, mais qui peuvent s'averer "efficasses" ) se retrouve dans le monde physique ne me gène pas.
mais que l'on dise :
bof, c'est comme n'importe quel autre nombre, non.

Je ne dis pas que c'est n'importe quel nombre, mais on ne le retrouve pas aussi syttématiquement. Car, on dirait que certains essaient de trop retrouver ce nombre en des endroits où il n'a pas de place (contrairement au coeur des tournesols).

les planêtes sont bien sphérique pour des raisons physiques , ce qui les amènent à avoir des proportions qui font intervenir pi.
celà ne choque personne, me semble-t-il.
et Pi intervient dans de nombreuses equations physiques , ( par uniquement en géométrie )
est-ce divin ? non !

Mais la quasi totalité des planètes sont rondes (aux effets de second ordre genre force centrifuge bien sûr).

[Fritz.Haber]

Cependant, comme le nombre d'or vaut approximativement 1,6180339887, son carré peut difficilement être égal à 1...

je n'ai pas dit que le nombre d'or au carré était égal à 1, j'ai dit que le nombre d'or au carré = le nombre d'or + 1 (et donc il est égal à 2,6180339887...)

[ansset]

@polo:
je crois que nous sommes d'accord.
ni sur-interprétation, ni deni de certaines corrélations.

en dehors de phi, les abeilles font bien des alvéoles "géometriques" ( hexagonales ) pour optimiser leur fonctions / l'espace occupé