D'où vient ce facteur 2 ?? (transformée de Fourier)

[fiatlux]

Bonsoir,

(Je précise au passage que cette question ressemble mais n'est pas la même que celle que j'ai posée sous le forum "informatique")

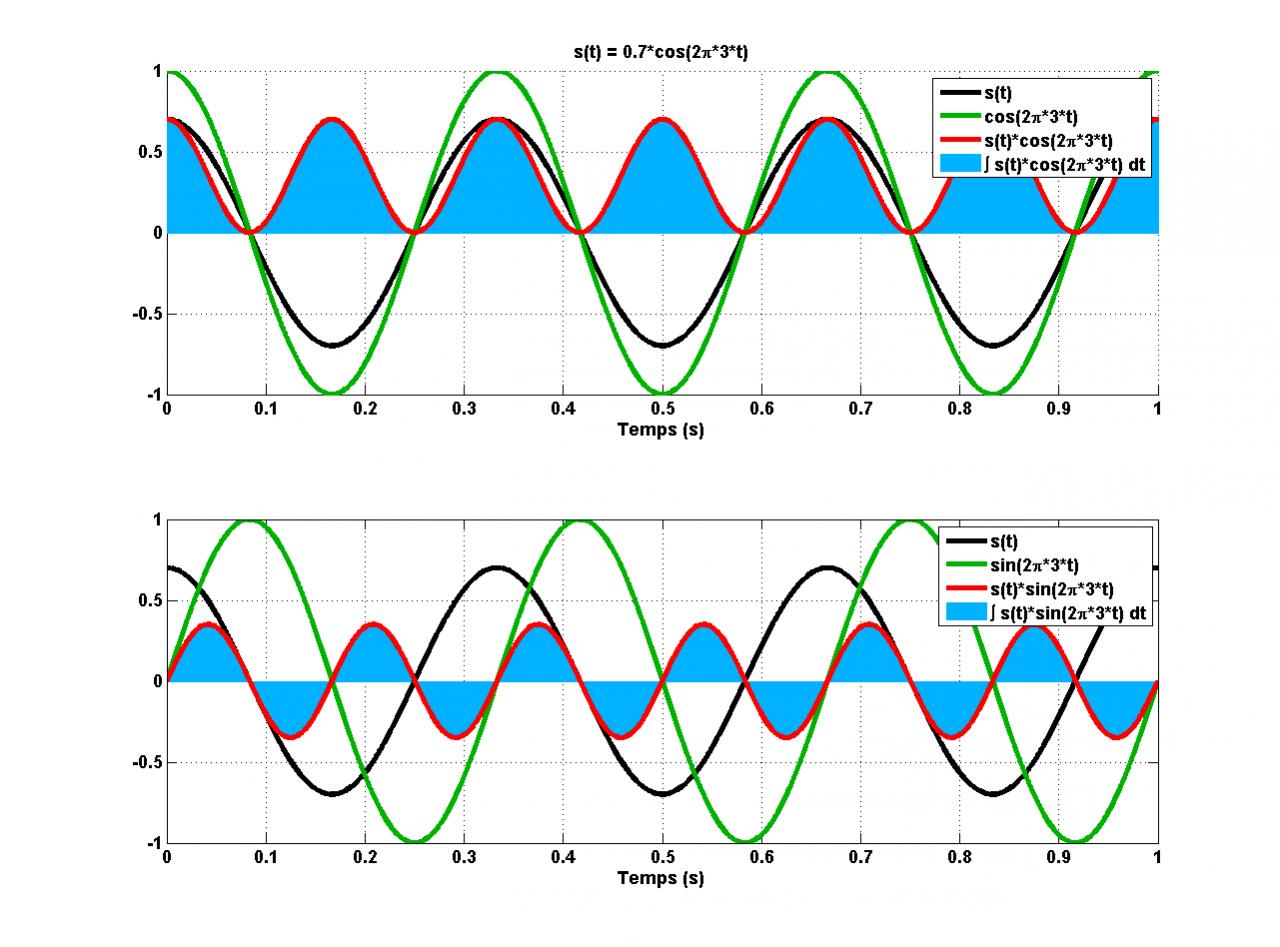
Admettons que j'ai un signal
Sa transfo de Fourier pour la fréquence f=3 Hz est donc:

Comme mon signal est un cosinus non-déphasé la 2e intégrale va me donner 0. La première intégrale me donne:

Une intégrale représentant l'aire sous la courbe, si j'évalue cette intégrale entre -1 et 1 ça fait 5 comme on peut voir ici:
http://www.wolframalpha.com/input/?i...tween+-1+and+1
Si j'évalue entre -3 et 3 ça fait 15
Entre -6 et 6 ça fait 30
Et ainsi de suite.
Donc entre -infini et +infini (comme le veut la formule de transfo de Fourier) ça me fait... l'infini. Jusque là d'accord. Donc si je fais une transfo de Fourier de mon signal, en f=3 j'aurai un pic infiniment grand... mais en pratique (dites-moi si je me trompe) l'aire totale sous la courbe ne nous intéresse pas. Ce qu'on veut c'est connaître l'ampli de notre signal (5 dans mon exemple). La question est donc: comme retrouver cette amplitude (5) à partir de l'aire sous la courbe de ??

Je me suis dit que, quand on fait cette intégrale, comme on multiplie un signal (qui a une certaine unité d'amplitude, disons des Volts) par un autre, puis encore par "dt", donc des secondes, la valeur de l'intégrale, autrement dit l'aire totale sous la courbe est en . J'imagine qu'il est donc logique par exemple de diviser cette aire sous la courbe par la durée (en secondes) du signal (pour se débarrasser des secondes), donc par exemple si on reprend les intégrales calculées avant:
--> entre -1 et 1 ça fait 5/2 = 2.5
--> entre -3 et 3 ça fait 15/6 = 2.5
--> entre -6 et 6 ça fait 30/12 = 2.5
Donc j'imagine que c'est logique, puisque ça me donne toujours le même résultat, qui est donc en Volts carré (). Mais alors comment retrouver mon amplitude recherchée (5 Volts) à partir de ces 2.5 Volts^2 ? Il semble qu'il y a toujours un facteur 2 entre le valeur en volts^2 et celle en volt, mais... pourquoi? Est-ce que ça a quelque chose à voir avec la valeur efficace de la tension ou quelque chose comme ça ? (désolé, mes souvenirs d'électronique sont assez lointains).

Merci beaucoup d'avance!
-----

[stefjm]

Bonjour,
Réponse rapide avant départ en vacances...

Je dirais que vous travaillez en complexe et que vous avez oublier la fréquence négative de votre cosinus dans l'expression.

D'où le facteur 2.

Cordialement.

[fiatlux]

Merci, mais je ne travaille pas en complexe. L’intégrale de droite (avec le sinus) est nulle, donc la partie imaginaire est nulle. Il ne reste que l’intégrale de gauche, que la partie réelle…

[fiatlux]

Quelqu'un ?...
Peut-être que c'est pas très clair. L'image ci-dessous devrait aider. En haut, l'aire en bleu vaut 0.35. Et non 0.7, comme je m'y attendrais, vu que c'est l'ampli de mon signal s(t). Et en bas c'est bien sûr 0, puisque je n'ai pas de sinus dans s(t).

[A voir en vidéo sur Futura]

[Antoane]

Bonjour,

Tu essayes d'intégrer un cos² sur |R, qui ne converges pas, donc tu te dis : "qu'à celà ne tienne, je ne vais en prendre qu'une partie"... c'est pas très rigoureux

Comme dit plus haut, le problème viens du fait que tu travailles en complexes : tu trouves donc une raie à 3Hz, mais si tu refais le calcul, tu trouveras une autre raie à -3Hz.
Ca vient de la définition de la série de Fourier :
en complexe : http://fr.wikipedia.org/wiki/S%C3%A9...ies_de_Fourier tu sommes sur Z,
alors qu'en réels : http://fr.wikipedia.org/wiki/S%C3%A9...nts_r.C3.A9els il y a un 2 devant l'intégrale et tu sommes sur N.


PS : les maths, c'est vraiment pas mon domaine (ça devrait, mais c'est pas )

[fiatlux]

Mmmh... ok :-S
Merci effectivement ça a l'air de venir de là ce facteur 2. Mais ça me laisse encore plus perplexe
J'ai jamais réellement compris ces histoires de fréquence négative... mais ça c'est une autre question.
T'aurais pas une explication "simple" ou intuitive disons de pourquoi y'a des fréquences négatives ?
J'ai cherchés sur internet, y'en a qui compare ça à une roue de voiture qui tourne à 3Hz, et le signe indique le sens dans lequel elle tourne... mais.... :-S

[Biname]

Bonsoir,


Donc entre -infini et +infini (comme le veut la formule de transfo de Fourier) ça me fait... l'infini. Jusque là d'accord. Donc si je fais une transfo de Fourier de mon signal, en f=3 j'aurai un pic infiniment grand... mais en pratique (dites-moi si je me trompe) l'aire totale sous la courbe ne nous intéresse pas. Ce qu'on veut c'est connaître l'ampli de notre signal (5 dans mon exemple). La question est donc: comme retrouver cette amplitude (5) à partir de l'aire sous la courbe de ??

Merci beaucoup d'avance!

Ben euh, c'est bêtement le 5 qui précède le cosinus ! Même au carré, le cosinus varie de 1 à 0 et le 5 qui multiplie le cosinus est l'amplitude.

Pour tout x : A.(sin f(x)^x), A est toujours l'amplitude ... non ????????

[fiatlux]

Euh... oui merci, mais c'était pas tout à fait ça la question
Dans mon exemple je sais que l'ampli est 5 puisque c'est moi qui l'ai choisie. Ce que je me demande, c'est comment la transformée de Fourier, elle, fait pour trouver que cette amplitude est 5. D'où le fait que j'ai essayé de reproduire ce que la TF fait, en multipliant mon signal avec un cosinus et un sinus, et en intégrant dans les 2 cas. Et systématiquement je trouvais une intégrale qui me donnait la moitié de l'amplitude de mon signal (2.5) au lieu de l'ampli correcte (5). D'où ma question: d'où vient ce facteur 2?

Et donc apparemment (cf réponse des 2 autres) c'est à cause du fait qu'un signal à fréquence f a une raie à -f et un raie à +f dans son spectre... et qu'en faisant ce que j'ai fait que je considère seulement la raie à la fréquence positive, donc je perds la moitié de l'énergie de mon signal... Et je trouve ça très perturbant ces fréquences négatives Si t'as une explication intuitive à me donner là-dessus je suis preneur.

[Burnus]

Pour t'aider dans ta réflexion:

cos(0) = - cos(pi) = cos(-pi)

A+

[Biname]

Euh... oui merci, mais c'était pas tout à fait ça la question
Dans mon exemple je sais que l'ampli est 5 puisque c'est moi qui l'ai choisie. Ce que je me demande, c'est comment la transformée de Fourier, elle, fait pour trouver que cette amplitude est 5. D'où le fait que j'ai essayé de reproduire ce que la TF fait, en multipliant mon signal avec un cosinus et un sinus, et en intégrant dans les 2 cas. Et systématiquement je trouvais une intégrale qui me donnait la moitié de l'amplitude de mon signal (2.5) au lieu de l'ampli correcte (5). D'où ma question: d'où vient ce facteur 2?

Et donc apparemment (cf réponse des 2 autres) c'est à cause du fait qu'un signal à fréquence f a une raie à -f et un raie à +f dans son spectre... et qu'en faisant ce que j'ai fait que je considère seulement la raie à la fréquence positive, donc je perds la moitié de l'énergie de mon signal... Et je trouve ça très perturbant ces fréquences négatives Si t'as une explication intuitive à me donner là-dessus je suis preneur.

Je viens de me retaper Fourier http://fr.wikipedia.org/wiki/S%C3%A9rie_de_Fourier
aller à 'Polynômes trigonométriques' (1)

... et ...

1) pour obtenir les coefficients de Fourier(1) = amplitude, il faut intégrer ta fonction entre -T/2 et +T/2 (T étant la période, ici 1/3) mais avec 1/T fois ta fonction f=3Hz >> T = 1/3 et T/2 = 1/6
2) on sort le 5 de l'intégrale et on va/doit trouver 1/2
3) la partie complexe est bien nulle pour f=3 : cos(6.pi.t).sin(6.pi.t) = (1/2).sin(12.pi.t) pour t = 1/6 ou T = -1/6 on a (1/2)sin(2.pi) = 0 CQFD_1
rappel : sin(a).cos(a) = (1/2)sin(2a)
4) il nous reste donc Wolfram (integrale (3 * cos²(6*pi*x) between -1/6 and 1/6) = 1/2 CQFD_2

Pour obtenir les coefficients de Fourier, Fourier(1) impose de faire varier n de moins infini à plus l'infini, on doit donc prendre la valeur 1 mais aussi la valeur -1
et avec -1 on trouve la fréquence négative qui se superpose farpaitement à la fréquence positive : cos(2.pi.f) + cos(-2.pi.f) = 2*cos(2.pi.f) CQFD_3

Et on a donc cette magnifique égalité 2 * 1/2 = 1

Pour te faire plaisir on va recherche le 5 et on a 5 * 1 = 5

Exercice : les choses eurent été bien différentes avec sin(6.pi.t)

Avec l'aide de Fourier qui a résolu le problème et de Wolfram qui intègre comme un chef, c'est un jeu d'enfant.

[Biname]

Je viens de me retaper Fourier http://fr.wikipedia.org/wiki/S%C3%A9rie_de_Fourier
aller à 'Polynômes trigonométriques' (1)

... et ...

1) pour obtenir les coefficients de Fourier(1) = amplitude, il faut intégrer ta fonction entre -T/2 et +T/2 (T étant la période, ici 1/3) mais avec 1/T fois ta fonction f=3Hz >> T = 1/3 et T/2 = 1/6
2) on sort le 5 de l'intégrale et on va/doit trouver 1/2
3) la partie complexe est bien nulle pour f=3 : cos(6.pi.t).sin(6.pi.t) = (1/2).sin(12.pi.t) pour t = 1/6 ou T = -1/6 on a (1/2)sin(2.pi) = 0 CQFD_1
rappel : sin(a).cos(a) = (1/2)sin(2a)
4) il nous reste donc Wolfram (integrale (3 * cos²(6*pi*x) between -1/6 and 1/6) = 1/2 CQFD_2

Pour obtenir les coefficients de Fourier, Fourier(1) impose de faire varier n de moins infini à plus l'infini, on doit donc prendre la valeur 1 mais aussi la valeur -1
et avec -1 on trouve la fréquence négative qui se superpose farpaitement à la fréquence positive : cos(2.pi.f) + cos(-2.pi.f) = 2*cos(2.pi.f) CQFD_3

Et on a donc cette magnifique égalité 2 * 1/2 = 1

Pour te faire plaisir on va recherche le 5 et on a 5 * 1 = 5

Exercice : les choses eurent été bien différentes avec sin(6.pi.t)

Avec l'aide de Fourier qui a résolu le problème et de Wolfram qui intègre comme un chef, c'est un jeu d'enfant.

oops

pour le point 3) j'ai oublie l'intégration
Wolfram(integrale 0.5*sin(12*pi*x) between -1/6 and 1/6) = 0 pas de partie complexe
mais ça ne change rien au résultat final

[stefjm]

Merci effectivement ça a l'air de venir de là ce facteur 2. Mais ça me laisse encore plus perplexe
J'ai jamais réellement compris ces histoires de fréquence négative... mais ça c'est une autre question.
T'aurais pas une explication "simple" ou intuitive disons de pourquoi y'a des fréquences négatives ?
J'ai cherchés sur internet, y'en a qui compare ça à une roue de voiture qui tourne à 3Hz, et le signe indique le sens dans lequel elle tourne... mais.... :-S

Bonjour,

T'as pas du chercher comme il faut...

Voici les fils en question :

http://forums.futura-sciences.com/ma...ml#post2023450

http://forums.futura-sciences.com/el...negatives.html

http://forums.futura-sciences.com/ph...ml#post4515614

Cordialement.