dérive yaw

[jamy311]

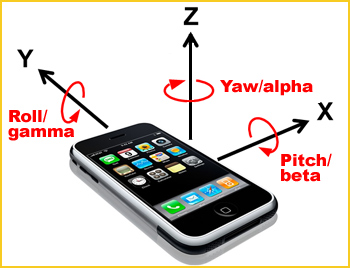
Bonjour, je travaille actuellement sur un bras mécanique 3 axes suivant le yaw/pitch/roll d'un téléphone via bluetooth.

Je programme l'acquisition et le traitement de la trame Bluetooth sur Arduino UNO couplé au module HC06.
L'émission de la trame se fait sous Android avec une application codée (si on peut appeler ça coder) sur App Inventor.

Pour les axes roll et pitch, j'utilise l’accéléromètre sur les axes X et Y avec un filtre de Kalman. Je n'ai aucun soucis sur ces deux axes.
Le problème intervient au niveau du yaw. J'emploie le orientation sensor (magnétomètre je suppose) pour connaitre le yaw du téléphone mais il dérive (surement exponentiellement) lorsque le téléphone n'est plus à niveau (logique étant donné que le principe est celui d'une boussole si je ne me trompe pas), c'est à dire lorsque le pitch et le roll sont différents de 0, orientés. De plus sur app inventor, avec le orientation sensor, on a une variable nommée magnitude variant de 0 à 1, 0 quand le téléphone est à niveau et 1 lorsqu'il est perpendiculaire.

Voilà ma question : n'y aurait-il pas une équation mathématique liant la magnitude et l'accéléromètre sur les axes X et Y pour compenser le drift du yaw ?
Je tiens à préciser que je suis prêt à lire toute piste, étant donné que cela fait longtemps que je tente des formules tirées par les cheveux.
Merci pour vos futures réponses.
-----

[PA5CAL]

Bonjour

Tout d'abord, comme nous sommes sur un forum français, il conviendrait d'éviter d'abuser des anglicismes, et donc d'employer les termes français qui conviennent (surtout quand leur existence et leur emploi sont séculaires). Ainsi, on parle de tangage (pitch) pour la rotation autour de l'axe droite-gauche, de roulis (roll) pour la rotation autour de l'axe avant-arrière, de lacet (yaw) pour la rotation autour de l'axe haut-bas, de dérive (drift) ou encore de capteur (sensor).


Les angles de lacet, de tangage et de roulis sont liés au référentiel du solide considéré (i.e. le téléphone portable), et non pas à un référentiel terrestre. En particulier, lorsque le solide est basculé de sorte que son axe de roulis se retrouve à la verticale, une rotation autour de l'axe vertical (haut-bas pour le référentiel terrestre) correspond à une modification de l'angle de roulis (avant-arrière pour le solide) et non pas de l'angle de lacet (haut-bas pour le solide). De même, la combinaison d'un angle de tangage de 90° et d'un angle de lacet de 90° est équivalente à la combinaison d'un angle de lacet de 90° et d'un angle de roulis de 90°. Pour cette raison, en principe on n'utilise pas ces trois angles pour représenter l'orientation du solide, mais au moins un angle lié au référentiel terrestre, qui est généralement la direction par rapport au nord sur une carte (donné par le magnétomètre) à la place de l'angle de lacet.

La magnitude est liée exclusivement à l'angle d'inclinaison de l'axe haut-bas du solide par rapport à la verticale. Dans la mesure où l'on exclut l'angle de lacet des informations d'orientation, la magnitude ne dépend plus que des angles de tangage et de roulis.


L'accéléromètre fournit une information d'accélération qui peut aussi bien provenir de la pesanteur que d'une modification de la trajectoire de l'accéléromètre dans l'espace. Par conséquent, ce capteur ne fournit des coordonnées qui correspondent à l'orientation du solide que lorsqu'il est fixe ou se déplace à vitesse linéaire constante.


Un magnétomètre n'a pas de raison de dériver exponentiellement, puisqu'une fois calibré, ce type de capteur indique la direction du nord magnétique et réalise donc une mesure absolue.

Il peut en revanche subir une déviation du fait d'une variation locale du champ magnétique terrestre, d'une perturbation par un autre champ magnétique, ou d'un calibrage imprécis (puisqu'il est en réalité constitué de plusieurs capteurs perpendiculaires). Mais cette déviation reste constante en l'absence d'évolution de sa cause.

Sa mesure peut également devenir inconsistante si elle n'est réalisée qu'en deux dimensions et que le champ magnétique terrestre est rendu perpendiculaire au plan de mesure. C'est très probablement la cause du symptôme décrit : si c'est réellement une dérive qu'on observe, alors celle-ci peut être due à l'utilisation du gyromètre du téléphone (dont l'angle d'orientation produit dérive effectivement dans le temps) afin de continuer à estimer une information qui n'est plus disponible de façon suffisamment précise.


En principe, pour pouvoir être déterminée dans tous les cas de figure, l'orientation d'un solide est calculée à partir de deux directions connues différentes dans l'espace. En l'occurrence, avec un accéléromètre et un magnétomètre on a :
- le vecteur de l'accélération de la pesanteur (qui correspond à peu près à la direction du centre de la terre), lorsque le capteur est fixe ou déplacé à vitesse linéaire constante,
- le vecteur du champ magnétique terrestre local.
Ces deux vecteurs sont nettement distincts lorsque le lieu n'est pas situé trop près des pôles. On peut considérer qu'à peu de chose près (car en pratique ce n'est pas rigoureusement exact), ces deux vecteurs appartiennent au plan vertical passant par le nord magnétique.

La mesure complète de ces deux vecteurs, qui fournit 6 valeurs, sert à déterminer les 3 angles souhaités. Les 3 valeurs qui apparaissent comme « en trop » correspondent d'une part au module et au sens des 2 vecteurs, et d'autre part à une information supplémentaire permettant de continuer de résoudre les équations du système dans le cas où l'orientation du solide mène à une indétermination ou à une trop grande imprécision (ce cas de figure survient notamment si l'on utilise un capteur à deux dimensions, lorsque le vecteur mesuré devient colinéaire avec l'axe manquant). Il n'y a donc pas vraiment d'information « en trop » : une bonne précision et une absence d'indétermination exigent a priori la mesure et l'exploitation de ces 6 valeurs.


Or, si l'on travaille à partir d'un nombre plus réduit d'informations déduites indirectement à partir des valeurs issues des capteurs, on risque d'avoir perdu des éléments pour pouvoir déterminer le résultat souhaité. En particulier, avec une boussole qui fournit juste un angle (issu d'une projection sur le plan horizontal ou bien de l'emploi d'un magnétomètre 2 axes), on doit forcément faire face à une indétermination lorsque cet angle devient inconsistant, et à une baisse de la précision quand on s'approche de cette situation. Et aucune formule ne pourra jamais corriger ce problème.

Par conséquent, pour pouvoir déterminer de façon convenable l'orientation du téléphone portable, il faudrait partir d'informations plus complètes, issues plus directement de ses capteurs (en admettant qu'il puisse effectivement les fournir).

[jamy311]

Tout d'abord, merci de votre réponse construite et de votre patience. Je tiens à m'excuser pour les termes employés, je traine plus sur des sites anglophones que francophones.

Ensuite, pour les angles du téléphone, j'utilise ceux ci-dessous (j'aurais du le préciser) :



Quand je parle de dérive, je me suis sans doute mal exprimé : en réalité, lorsque le téléphone est immobile, le magnétomètre ne subit aucune dérive. Le problème vient lorsque j'oriente le téléphone sur les axes roulis ou tangage au lieu de les laisser à niveau.

De plus, je suis presque persuadé qu'il est possible de compenser cette "dérivation" par la magnitude, je vais essayer de mettre toutes mes données sur un graphique et des tableaux pour mieux comprendre le problème (je ne sais pas encore comment m'y prendre mais je vais trouver).

Au niveau de mes propos sur la dérive exponentielle, ce n'est que purement pas ressenti et tout cela sera plus clair si j'arrive à obtenir des courbes.

Je posterais éventuellement mes résultats si aboutis.

[jamy311]

Voila les graphiques promis (avec en bleu la courbe obtenue et en orange la courbe souhaitée) :

graph1.png

graph2.png

graph3.png

Malgré les paramètres différents entre chaque courbe, celles-ci sont très similaires. Peut-être que le roulis et la magnitude sont liés.
Dans tous les cas, le phénomène dont je parlais est effectivement présent : lorsque le roulis augmente, le lacet diminue.

Je peux apporter d'autres données si souhaité.

A présent, je vais tenter d'obtenir une(des) équation(s) s'approchant de mes courbes afin de compenser cette dérivation.

[A voir en vidéo sur Futura]

[jamy311]

Finalement je ferme ce topic car j'ai réussi à modéliser l'équation du lacet en fonction de la magnitude. Comme quoi c'était possible.

[PA5CAL]

Si le (soi-disant) angle de lacet doit dépendre de la (soi-disant) magnitude, alors il me semble qu'il y a un problème entre la définition de ces valeurs et les valeurs prise en compte.

Il me paraît donc nécessaire de s'intéresser à ce que ces termes sont censés représenter réellement et à la relation qui doit théoriquement les lier, afin de les comparer aux valeurs produites par le téléphone. Soit les calculs effectués par le téléphone pour les produire à partir des mesures des capteurs embarqués sont faux (ce qui est peu probable, mais pas complètement impossible), soit les termes utilisés sont inappropriés et l'usage des valeurs correspondantes risque de l'être également.

Je note d'ailleurs que la documentation du système de capteurs sous Android ne fait pas référence au lacet (yaw) mais à l'azimut (azimuth, c'est-à-dire l'angle dans le plan horizontal entre la direction du nord magnétique et l'axe de roulis). Sa valeur apparaît comme première coordonnée du « vecteur orientation ».

Il serait aberrant de se livrer à un bricolage obscur des valeurs produites pour atteindre les résultats souhaités. Notamment, si l'on ne comprend pas ce qu'on fait, rien ne garantit que la relation trouvée expérimentalement soit encore applicable quand la situation aura changé (autre lieu, autre téléphone, après re-calibrage ou mise à jour du logiciel, etc.).

Quoi qu'il en soit, il faudrait au moins clarifier ce point afin que cette discussion puisse servir aux futurs lecteurs.

[jamy311]

Je comprends tous les termes que j'emploie, parfois avec un petit manque de rigueur, certes, mais inutile de tout m'expliquer, je sais comment fonctionne ces capteurs (dans mon cas, l'azimut joue le rôle du lacet lorsque le téléphone est à niveau, ce que je précise plusieurs fois il me semble).
Je précise également que les valeurs reçues sont celles données par App Inventor, et c'est pourquoi il est inutile de dire sans arrêt que mes valeurs sont aberrantes, les graphiques étant la preuve du contraire. Pour conclure, j'ai obtenu par Regressi l'équation d'une parabole du lacet (azimut) en fonction de la magnitude et que j'ai réussi à compenser les dérivations du lacet, réussi concrètement, avec des tests directs sur le bras robotisé.
Pour terminer, étant donné que j'ai trouvé réponse à ma question, il est inutile d'alimenter ce topic et mes travaux n'ont rien de bricolages mais plutôt d'expérimentations.
Bonsoir.

[PA5CAL]

dans mon cas, l'azimut joue le rôle du lacet lorsque le téléphone est à niveau

Ça c'est vrai dans tous les cas. Mais lorsque le téléphone n'est plus à niveau, le lacet est différent de l'azimut. Tu conviendras j'espère que l'emploi d'un terme à la place de l'autre est forcément erroné et qu'il a potentiellement comme conséquence d'employer les mauvaises formules ou d'aboutir à de mauvais résultats.

Ce qui est sûr, c'est que pour l'instant on ne sait pas ce que produit vraiment App Inventor, et que si on le savait on aurait déjà pu déterminer analytiquement les formules analytiques pour obtenir les résultats souhaités et les éventuels situations d'indétermination et d'imprécision que j'ai évoquées.

Pour terminer, étant donné que j'ai trouvé réponse à ma question, il est inutile d'alimenter ce topic et mes travaux n'ont rien de bricolages mais plutôt d'expérimentations.

Une équation trouvée par une méthode de régression sur un nombre réduit de mesures faute de connaître les détails d'un système qui a forcément été entièrement spécifié, matériellement et logiciellement, c'est vraiment ce qu'on peut appeler du bricolage. Pour info, dans un cadre professionnel, ce genre d'approximation peut valoir d'être viré.

Enfin, la finalité de ce forum public est de partager les questions et les réponses apportées afin d'en faire profiter les futurs lecteurs. Laisser la discussion en plan sans avoir cadré expressément le problème ni la réponse, ce n'est pas ce qui motivera les contributeurs à continuer de t'apporter leur aide.

[PA5CAL]

Petit exemple pratique : voici trois courbes différentes donnant censément la « magnitude » en fonction de l'angle. Deux d'entre elles sont des paraboles obtenue expérimentalement, par régression polynomiale à partir de séries de mesures relevées sur un smartphone. L'autre correspond à la fonction théorique qu'on trouve dans le code d'Android.

 Cliquez pour afficher

La courbe en bleu est celle de la fonction théorique.

Ce n'est pas une parabole, c'est une sinusoïde.

[jamy311]

Merci (et merci aussi pour votre patience, je suis légèrement borné), je serais intéressé d'avoir un lien qui me mènerait à cette sinusoïde pour l'étudier de plus près. J'ai bel et bien une parabole car mes données sont organisées différemment dans un intervalle relativement très réduit ([0;1]) mais mes relevés expérimentaux sont de mauvaises qualités donc on ne sait jamais.

Ensuite, il est sûr que mes résultats pourraient être assimilés à des bricolages dans la mesure où je n'ai ni le savoir, ni les moyens d'entreprendre de tels expérimentations, j'applique le (très) peu que je puisse savoir du haut de mon niveau terminale.

Pour finir, si je comprends bien, on a ici sur vos exemples la magnitude en fonction du lacet, il serait donc possible de trouver l'équation de cette courbe et l'exploiter pour réussir à compenser la dérive de l'azimut en fonction de la magnitude, me trompe-je ?

[jamy311]

Après des tests, avec un filtre de Kalman précis appliqué sur l'azimut, la dérive n'a lieu que lorsque le roulis change d'angle entre [-90;90] et le lacet entre [0;180].
Voici mes résultats :

graph5.png

graph6.png

Avec en bleu la courbe représentant les valeurs de l'azimut en fonction de la magnitude (non traitées) et en bleu les mêmes valeurs mais compensées avec une équation. Ce n'est pas terrible mais ça va déjà atténuer pas mal les dérives. Je pourrais obtenir un R² plus proche de 1 mais cela impliquerait des fonctions polynomiales de plus haut degré ce qui pourrait ralentir le système.