Salut,
Je te propose un correcteur par placement de pôle. C'est une méthode que je trouve plus facile à mettre en oeuvre qu'un PID.
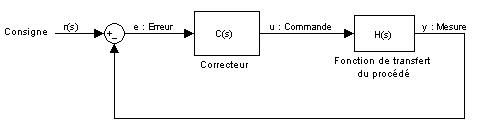
Si tu écris la fonction de transfert en boucle fermée de ce correcteur :
Et en isolant, le correcteur, son expression est donnée par :
Ton cahier des charges, c'est Gamma, il est connu car c'est à toi de le définir. Par contre, il faut que le correcteur soit réalisable : l'ordre du dénominateur doit être supérieur ou égal à l'ordre du numérateur. Il y a également des conditions sur les zéros du processus qui doivent être stables, (car maintenant les zéros se retrouvent au dénominateur), mais ici c'est le cas.
Alors maintenant comment définir Gamma ?
Comme dit plus haut le correcteur doit être réalisable, donc Gamma doit être une fonction de transfert du second ordre. Par conséquent, il faut choisir les deux paramètres ksi et omega. Ksi est facile à choisir : il détermine ton dépassement. Un ksi = 0.707 correspondra à un dépassement transitoire de 5% au dessus la valeur finale. Ensuite, pour omega, tu peux dans un premier temps prendre le même que ton processus, puis tu ajustera sa valeur par simulation
-----