
- Forum
- Futura-Sciences : les forums de la science
- MATHEMATIQUES
- Mathématiques du collège et du lycée
- Problème de x^x
Problème de x^x
- 20/08/2007, 22h20 #31Médiat
- Date d'inscription
- août 2006
- Âge
- 75
- Messages
- 20 617
Re : Problème de x^x
------
Je suis Charlie.
J'affirme péremptoirement que toute affirmation péremptoire est fausse
- 20/08/2007, 22h30 #32FonKy-
- Date d'inscription
- juin 2007
- Localisation
- Stockholm
- Âge
- 38
- Messages
- 1 755
Re : Problème de x^x
oui je sais j'y suis aller mais j'aurai aimer que tu me developpe tout ca
J'allais dire des trucs mais je m'embrouille un peu, tout dépend avec quoi on dérive.
Je comprend mieux ce que tu voulai dire en fait apr c'est pas la peine, en fait on a n! qui est une suite de factorielle donc on peux evidement pas deriver :/ c'est balot. A moins de définir la dérivé comme
 enfin je sais pas ce sont juste des propositions
enfin je sais pas ce sont juste des propositions 
quoi ? chacun son délire mathématique
FonKy-
- 20/08/2007, 22h37 #33invitec053041c

- Date d'inscription
- janvier 1970
- Messages
- 4 537
Re : Problème de x^x
oui je sais j'y suis aller mais j'aurai aimer que tu me developpe tout ca
J'allais dire des trucs mais je m'embrouille un peu, tout dépend avec quoi on dérive.
Je comprend mieux ce que tu voulai dire en fait apr c'est pas la peine, en fait on a n! qui est une suite de factorielle donc on peux evidement pas deriver :/ c'est balot. A moins de définir la dérivé comme
 enfin je sais pas ce sont juste des propositions
enfin je sais pas ce sont juste des propositions 
quoi ? chacun son délire mathématique
FonKy-
Et après c'est toi qui me demandes si je viens de me lever .
.

- 20/08/2007, 23h01 #34invite6bacc516

- Date d'inscription
- janvier 1970
- Messages
- 450
Re : Problème de x^x
Je l'ai tracée sur calculatrice et non, ça y ressemble mais ce n'est pas une parabole regarde bien :þ Pour ce qui est de l'exponentielle, pas très compliqué, dit toi que c'est une suite géométrique comme n'importe laquelle

- 20/08/2007, 23h43 #35inviteec581d0f

- Date d'inscription
- janvier 1970
- Messages
- 900
Re : Problème de x^x
Je vois que j'étais nul sur ce coup là
 hahaha Merci de m'avoir éclairé Dydo
hahaha Merci de m'avoir éclairé Dydo 

- 20/08/2007, 23h49 #36invitec053041c

- Date d'inscription
- janvier 1970
- Messages
- 4 537
Re : Problème de x^x
L'exponentielle n'est pas une suite mais une fonction de IR dans IR+ .
.
"Comme n'importe laquelle": tu es méchant ! Elle a quand même la propriété d'être égale sa fonction dérivée !
- 20/08/2007, 23h51 #37invite6bacc516

- Date d'inscription
- janvier 1970
- Messages
- 450
Re : Problème de x^x
Oups pardonne moi du blasphème, j'oubliais ce détail tellement j'en ai mangé :þ Et oui, j'avais oublié de préciser que c'était une fonction, mais bon, on va dire qu'on s'est comprit ^^
( 2 fautes sur une seule phrase, effectivement c'est dur :P )
- 21/08/2007, 00h01 #38invitec053041c

- Date d'inscription
- janvier 1970
- Messages
- 4 537

- 21/08/2007, 00h03 #39inviteec581d0f

- Date d'inscription
- janvier 1970
- Messages
- 900
Re : Problème de x^x
 j'étais content d'avoir cru comprendre (dur a la détente) mais je retombe dans le gouffre du non-savoir
j'étais content d'avoir cru comprendre (dur a la détente) mais je retombe dans le gouffre du non-savoir 


- 21/08/2007, 00h08 #40invite6bacc516

- Date d'inscription
- janvier 1970
- Messages
- 450
Re : Problème de x^x
Ma mauvaise formulation ne doit pas changer grand chose si tu avais comprit, dans une suite géométrique tu passes du terme au suivant en le multipliant par une raison
 ; ainsi tu as, en général :
; ainsi tu as, en général :

 avec
avec  et
et  fixés.
fixés.
He ben l'exponentielle, c'est pareil, mais c'est une fonction définie sur IR et non une suite, simplement définie sur IN. En gros tu as :
 avec
avec  un certain nombre fixé lui aussi :þ
un certain nombre fixé lui aussi :þ
Après le fait que la fonction soit sa propre dérivée c'est une propriété remarquable de la fonction ( on la définit à partir de ça même, du moins en Terminale ); mais fondamentalement, c'est la même chose, une fonction géométrique

- 21/08/2007, 00h23 #41inviteec581d0f

- Date d'inscription
- janvier 1970
- Messages
- 900
Re : Problème de x^x
D'accord
 Merci alors
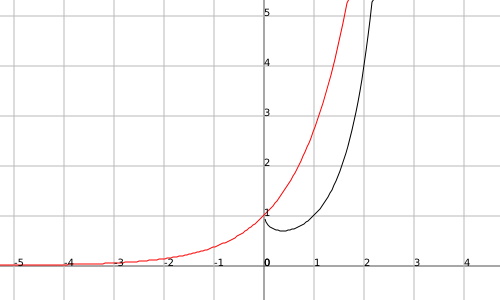
Merci alors  mais en quoi cette fonction est-elle proche de celle que j'ai tracé sur ma calculatrice ?? Si cette fonction
mais en quoi cette fonction est-elle proche de celle que j'ai tracé sur ma calculatrice ?? Si cette fonction
http://fr.wikipedia.org/wiki/Image:C...onentielle.jpg
est proche de f(x) = x^x
il me faudra soit de nouvelles lunettes soit une nouvelle calculatrice.

- 21/08/2007, 00h28 #42invite6bacc516

- Date d'inscription
- janvier 1970
- Messages
- 450
Re : Problème de x^x
Pas vraiment non, elle va croître beaucoup plus rapidement, ce n'est plus une fonction géométrique puisque la base n'est plus fixée, la variable est la puissance de la variable même, donc les deux croient en même temps, alors que pour l'exponentielle, ou toute autre fonction géométrique, ça reste de la forme :

Et compare les deux sur ta calculatrice, tu verras bien qu'il y a une différence, ne serait-ce qu'au début de l'intervale où on l'a définie, elle décroit :þ
- 21/08/2007, 00h35 #43inviteec581d0f

- Date d'inscription
- janvier 1970
- Messages
- 900

- 21/08/2007, 10h13 #44invite43bf475e

- Date d'inscription
- janvier 1970
- Messages
- 301
Re : Problème de x^x
d'ailleurs le min de f(x)=x^x est atteind pr x=e^-1=1/e.
Et a^x=e^alnx
Petit complément pour les fonctions géométriques a bases fixées

- 21/08/2007, 13h55 #45inviteec581d0f

- Date d'inscription
- janvier 1970
- Messages
- 900
Re : Problème de x^x
C'est bienEt a^x=e^alnx ou bien
ou bien 



- 21/08/2007, 14h05 #46FonKy-
- Date d'inscription
- juin 2007
- Localisation
- Stockholm
- Âge
- 38
- Messages
- 1 755
Re : Problème de x^x
ben

vi milas le min est e-1
FonKy-
- 21/08/2007, 14h13 #47inviteec581d0f

- Date d'inscription
- janvier 1970
- Messages
- 900
Re : Problème de x^x
??????
Pourquoi et non
et non 
et merci FonKy-
- 21/08/2007, 14h19 #48invite43bf475e

- Date d'inscription
- janvier 1970
- Messages
- 301
Re : Problème de x^x
En ft le logarithme népérien ln(x) est la réciproque de l'exponentielle e^x es decir :
x=e^(lnx)=ln(e^x), x appartenant à IR
- 21/08/2007, 14h39 #49invite6bacc516

- Date d'inscription
- janvier 1970
- Messages
- 450
Re : Problème de x^x
C'est juste pour illustrer l'"annulation" des fonctions réciproques
 et
et  , par contre tu as raison, on parle d'exponentielle dont ça serait plutôt
, par contre tu as raison, on parle d'exponentielle dont ça serait plutôt  , mais pour l'application c'est pareil :þ :
, mais pour l'application c'est pareil :þ :
 ( Fonction puissance il me semble )
( Fonction puissance il me semble )
 (
(  , exponentielle de base
, exponentielle de base  )
)
Mais ici on parlait bien de l'exponentielle de base x ( ) puis de base quelconque, mais apparemment certains se sont laissés embrouiller
) puis de base quelconque, mais apparemment certains se sont laissés embrouiller  ( j'en suis pas loin hein ^^ ).
( j'en suis pas loin hein ^^ ).

- 21/08/2007, 15h37 #50FonKy-
- Date d'inscription
- juin 2007
- Localisation
- Stockholm
- Âge
- 38
- Messages
- 1 755

- 21/08/2007, 15h40 #51FonKy-
- Date d'inscription
- juin 2007
- Localisation
- Stockholm
- Âge
- 38
- Messages
- 1 755

- 21/08/2007, 15h41 #52invite43bf475e

- Date d'inscription
- janvier 1970
- Messages
- 301
Re : Problème de x^x
Pardonne mon ignorance mais nn! je ne vois pas ...

- 21/08/2007, 15h44 #53invite6bacc516

- Date d'inscription
- janvier 1970
- Messages
- 450
Re : Problème de x^x
Je me permet de t'éclairer en simplifiant la chose :þ

Normalement ça doit bloquer quelque part

- 21/08/2007, 15h44 #54FonKy-
- Date d'inscription
- juin 2007
- Localisation
- Stockholm
- Âge
- 38
- Messages
- 1 755
Re : Problème de x^x
ah oui tu es en Premiere .. mais dans ce cas tu es quand meme gonflé de poser des affirmations

regarde les ensembles de définitions de toutes les fonctions que tu utilises
FonKy-
edit: dydo tu n'as pas l'air de maitriser le latex

- 21/08/2007, 15h48 #55invite6bacc516

- Date d'inscription
- janvier 1970
- Messages
- 450

- 21/08/2007, 15h49 #56invite43bf475e

- Date d'inscription
- janvier 1970
- Messages
- 301
Re : Problème de x^x
pr répondre à ta question fonky, ln x est definie sur IR+*, à valeurs dans IR, et e^x, définie sur IR, à valeur dans IR+*, non je ne suis pas en premiere, mais en TS, du moins j'en sors, en ft je viens de m'appercevoir de ma faute, pour x=e^(ln x), x doit être dans IR+*...
Dsl c'est pas ma journée...
- 21/08/2007, 18h53 #57invitec053041c

- Date d'inscription
- janvier 1970
- Messages
- 4 537
Re : Problème de x^x
Bon, je persiste à dire qu'une "fonction géométrique" n'existe pas
 .
.
Il vaut mieux parler de fonction puissance.
On peut en effet la définir autrement que par une équation différentielle Envoyé par Dydo Après le fait que la fonction soit sa propre dérivée c'est une propriété remarquable de la fonction ( on la définit à partir de ça même, du moins en Terminale );
Envoyé par Dydo Après le fait que la fonction soit sa propre dérivée c'est une propriété remarquable de la fonction ( on la définit à partir de ça même, du moins en Terminale ); .
.

- 21/08/2007, 19h15 #58invite6bacc516

- Date d'inscription
- janvier 1970
- Messages
- 450

- 21/08/2007, 19h43 #59invitec053041c

- Date d'inscription
- janvier 1970
- Messages
- 4 537
Re : Problème de x^x
On peut par exemple définir l'exponentielle comme:

On peut même mettre pour tout z appartenant à C. Bref, ça n'est pas l'objet du fil mais c'était pour te montrer que la définition de TS n'est pas la seule.
Au final , on tombe bien sur la même fonction, c'est le principal .
.

- 21/08/2007, 19h56 #60FonKy-
- Date d'inscription
- juin 2007
- Localisation
- Stockholm
- Âge
- 38
- Messages
- 1 755
Re : Problème de x^x
Je comprend meme pas le rapport entre l'exponentielle et une suite ou "fonction" géométrique ..

Discussions similaires
-
Problème brachistochrone ou autrement dit le problème du toboggan idéal...
Par invitee2512ce2 dans le forum PhysiqueRéponses: 11Dernier message: 26/05/2011, 13h27 -
Un petit problème qui me pause problème lol
Par invitef2853e5d dans le forum Mathématiques du supérieurRéponses: 13Dernier message: 31/03/2009, 16h28 -
problème avec un lecteur mp4(le problème vient de l'ordinateur)
Par inviteaca1b987 dans le forum Matériel - HardwareRéponses: 3Dernier message: 29/10/2007, 17h53 -
TPE : le problème de la problématique... pose problème
Par invitedea46a4f dans le forum TPE / TIPE et autres travauxRéponses: 0Dernier message: 21/09/2006, 19h45
Fuseau horaire GMT +1. Il est actuellement 04h49.


 )
)