si m = 1500
combien vaut n, et comment le calcule t'on ?
en passant par des logarithmes en factorisant par la puissance (1/n) ?
merci.
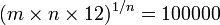
-----

si m = 1500
combien vaut n, et comment le calcule t'on ?
en passant par des logarithmes en factorisant par la puissance (1/n) ?
merci.
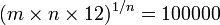


Salut,
Je pense que passer au logarithme est une bonne idée, car tu sais que :
et que
Pense aussi à décomposer 100000 et 18000.

Bon ben j'étais mal réveillé et j'avais pas mangé !!!
car d'une part ce que j'ai exposé est trés simple il suffit de multiplier les deux membres par N et la solution devient triviale.
J'ai ensuite chercher à calculer le véritable exercice et j'ai aussi trouvé, comme quoi un bon repas...
Meme pas besoin de Logarithmes dans tout ça.

salut
peux-tu m'expliquer comment faire sans utiliser le logarithme?


Salut,
Je ne sais pas ce que tu entends par "multiplier par n", mais dans une puissance, il ne suffit pas de multiplier...
, pas


Il devait vouloir dire : élever les deux membres de l'égalité à la puissance n.
On trouve des chercheurs qui cherchent ; on cherche des chercheurs qui trouvent !

et comment faire dans ce cas sans utiliser le logarithme.

je me suis mal exprimé.
On élève à la puissance n chaque membre, puis on simplifie avec les logarithmes, on a donc effectivement besoin des logs.
Merci de m'avoir relu, ca prouve que j'ai retenu votre attention et qu'il y a des gens bienveillant sur ce forum
J'ai retrouvé l'équation de base :
avec :
si
on a :
le problème est qu'en résolvant l'équation je trouve un n négatif.
Alors que je suis censé trouver un résultat positif.
Cette formule est censé calculer les mensualités d'un crédit à la banque sous la forme :
Valeur initiale d'emprunt
le taux d'intêret
les annuités
les mensualités
la valeur finalement payé en terme de l'échéancier

Voici le cheminement de mon calcul dites moi ou je fais fausse route et surtout pourquoi !!!
en divisant chacun des membres par n on a :
ensuite on a :
en passant au Logarithmes de chaque coté on obtient :
d'où :
donc n vaut :
ce qui est négatif


J'ai peut-être mal compris le truc, mais Vi a quelle valeur ?
Et la formule que tu utilises est-elle déjà donnée ou c'est toi qui l'as écrite ?
Pour le moment, je ne vois pas d'erreur dans ton raisonnement (j'me trompe peut-être), ça pourrait venir de plus haut ?

Vi vaut 100000 euros par exemple.
C'est une formule que j'ai trouver sur wikipédia.


Chuis bête, j'ai trouvé -____-
Quand tu divises 1.04^n par n, ça fait 1.04^(n-1) ??
Pour la formule trouvée sur wikipedia, je ne sais pas si elle est adaptée...pour le moment, je n'y vois pas de solution analytique oO
Peux-tu donner l'énoncé exact de ton exo ? =)





Justement, je doute que ta valeur finale soit égale à nxmx12
L'énoncé please ? ^^

Oups...
Vf est forcément égale à n x m x12, car la valeur finale vaut forcément la multiplication de la mensualité du crédit multiplié par 12 pour l'avoir sur une année et multiplié par n pour l'avoir sur la durée totale du crédit.
Vf est la somme totale que l'on donnera a la banque elle vaut bien le nombre totale de mensualités percue par la banque !!!

Ok donc si je reprends mon calcul voici ce que j'ai :
en divisant chacun des membres par n on a :
ensuite on a :
Par contre là je suis bloqué


Je comprends pas pourquoi cet emploi soudain d'une formule faisant intervenir le taux d'intérêt qui semble n'avoir aucun lien ici. C'est à cause d'une certaine ressemblance, parce qu'il y a une puissance 1/n ? Le problème ici, c'est que ton égalité fait intervenir n non seulement en puissance, mais également dans le premier membre. A priori, c'est pas triviale comme solution.

oui pas si triviale que ça la solution en effet.
Bref si quelqu'un peut m'aider je suis preneur.


Maple trouve cela:
Apperement la fonction LambertW vérifie:
LambertW(x) * exp(LambertW(x)) = x;
Mais apres je sais pas si c'est le bon résultat.
MAple me sort cela apres avoir tapé:
solve((m*n*12)^1/n,n);

