Bonjour à tous!
Voilà j'ai un dm de maths à faire sur Exel entre autre dans le cadre des nouvelles épreuves de maths au bac, c'est donc un entrainnement.
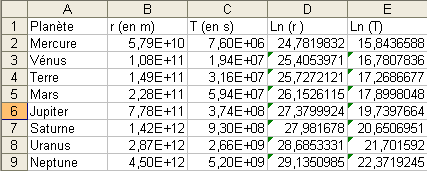
On me donne 8 planètes avec pour chaque sa période de révolution et le rayon de l'orbite considérée comme circulaire
1)Entrer sur une feuille de calcul d'un tableur les données (cf mon tableur ci dessous)
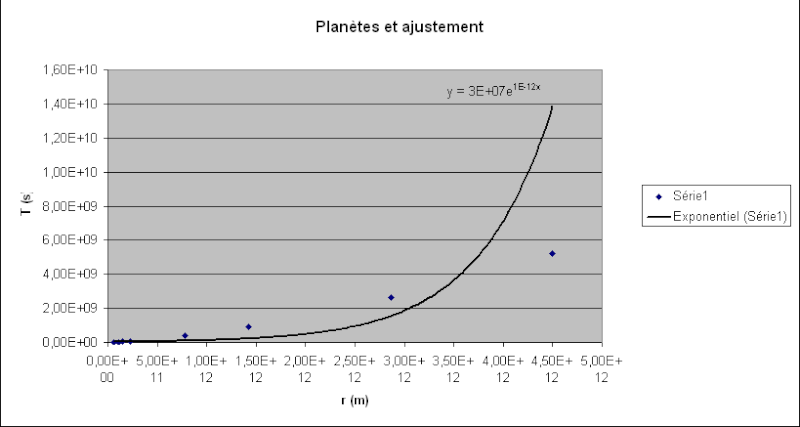
Tracer la courbe représentant la période T en fonction du rayon r (cf courbe 1)
Par contre pour cette courbe j'ai un problème avec l'ajustement exponentiel, une de mes amies m'ayant dit que la sienne passait par tous les points. Où ai-je fais une erreur?
Combien de point apparaissent sur le graphique?J'en ai mis 5
Que constatez vous? C'estun phénomène physique qu'ils demandent c'est quoi? Une amie a mis qu'ils les avaient rangées dans l'ordre croissant d'où l'évolution de la courbe mais j'suis pas convaincue
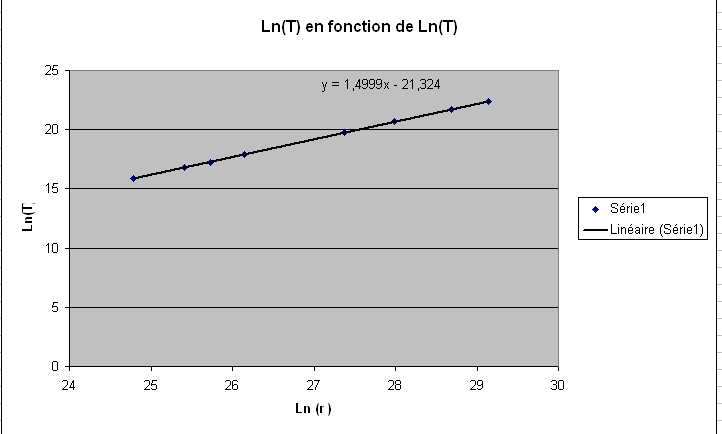
2) Faire afficher le graphique donnant ln(T) en fonction de Ln(r) (cf courbe 2)
Combien de points apparaissent sur le graphique et que constatez vous?
Je vois 8 points mais je comprends pas ce qu'on veut me faire dire mis à part qu'avec Ln on les vois tous clairement?
3) Determinez à l'aide du tableur le coefficient directeur d'une droit qui permet de donner un ajustement des points représentés
On me demande l'équation de la premiere courbe là? Mais comme elle ne passe par par tous les points :S. Ou alors faut-il prendre l'équation de la courbe des Ln? Mais dans ce cas j'ai aussi un problème dans l'équation que me donne exel l'ordonée à l'origine semble être négative
4) En déduire que pour les 8 planètes étudiées T= k (racine de r)^3 où k est une constante réeelle. Vérifiez avec le tableur.
Vu que j'ai pas compri la question d'avant je rame pour celle là et je ne vois pas du tout comme justifier avec exel
Voilà vous ai mis mes pistes de reflexions, merci par avance de votre aide!
-----







 Pour moi les 8 apparaissent
Pour moi les 8 apparaissent 







