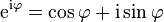Nombre complexe : Notation exponentielle
Discussions similaires
-
Par invited8225f2d dans le forum Mathématiques du collège et du lycée
Réponses: 2
Dernier message: 09/04/2008, 23h51
-
Par invite58a61433 dans le forum Mathématiques du supérieur
Réponses: 0
Dernier message: 27/02/2008, 00h45
-
Par invite2c7c5c2e dans le forum Mathématiques du collège et du lycée
Réponses: 10
Dernier message: 27/01/2008, 17h52
-
Par invitef1068ed6 dans le forum Mathématiques du collège et du lycée
Réponses: 1
Dernier message: 22/05/2007, 18h58
-
Par invite87a1ce41 dans le forum Mathématiques du supérieur
Réponses: 9
Dernier message: 16/04/2005, 14h20





 sous la forme
sous la forme