Demonstration de l'irrationalité de E Par la Recurrence

[invite693d963c]

Bonjour à tous,
Je vous fais part de ce post afin d'avoir quelques conseils pour résoudre un exercice.
Il s'agit des questions 5 et 6 de scan ( En haut de la feuille) ci-dessous,

C'est un exercice d'un de mes Dm de recherche cad qu'on effectue ce Dm avant d'avoir le cours (Sur les suites dans mon cas)
Mhh..... J'ai longtemps cherché sur ces exercices et il en sort ( selon moi) :

Questions 5
La methode que j'utilise est classique : Verification, Supposition et Demontration.

Verification : J'ai verifié pour n=1, ce qui donne,
1-x < epx(-x) < 1-x +x^2/2!

Donc, J'ai créé 2 fonctions tel que :
f(x) = exp(-x) - 1+ x
h(x) = exp(-x) -(1-x+x^2/2!)
Auxquelles j'ai fais subir une etude de signe et de variations ( etudes de fonctions classiques)
Et J'arrive à la conclusion que n=1 est vraie

Supposition : Au rang no+ 1, on aurait ,

Pno+1 : 1- x + ... + ?? < exp(-x) < 1-x + ... + x^(2no)/(2no!) + ??
Les " ??" corresponderaient à des Nouveaux termes que je n'ai pas Trouvé

Demonstration : Vide Total

En espérant avoir une aide de votre part, Je vous remercie d'avance
-----

[invite693d963c]

J'hésite cependant entre 2 Méthodes qui sont : La récurrence sur des entiers Simples et La Récurrence d'ordre n.

En effet, Je note que pour n pair on ajoute une expression différente de n impaire. Donc J'utiliserais la Récurrence d'ordre 2 pour cet exercice ...
De plus, Si je peux montrer qu'avec n+1 ( n etant pair), j'arrive à une expression de la forme n impair. Alors, j'utiliserais la réccurence sur des entiers simples ...

Je suis partagé


Faut-il Faire 2 cas isolés

La récurrence sur des entiers Simples

Pour démontrer une propriété portant sur tous les entiers naturels, comme par exemple la formule du binôme de Newton, on peut utiliser un raisonnement par récurrence. Notons la propriété en question P(n) pour indiquer la dépendance en l'entier n. On peut alors l'obtenir pour tout entier n en démontrant ces deux assertions :

* P(0) (0 vérifie la propriété) : c'est l'initialisation de la récurrence ;
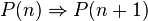* Pour tout entier n, c'est l'hérédité.

On dit alors que la propriété P s'en déduit par récurrence pour tout entier n. On précise parfois « récurrence simple », quand il est nécessaire de distinguer ce raisonnement d'autres formes de récurrence (voir la suite).

Le raisonnement par récurrence est une propriété fondamentale des entiers naturels, et c'est le principal des axiomes de Peano. Une axiomatique est, en quelque sorte une définition implicite, dans ce cas une définition implicite des entiers naturels. Dans certains contextes, comme en théorie des ensembles on déduit directement la récurrence de la définition, explicite cette fois, de l'ensemble des entiers naturels.

La récurrence peut aussi s'exprimer de façon ensembliste : il s'agit juste d'une variation sur la définition d'un ensemble en compréhension. On associe à une propriété P l'ensemble E des entiers naturels la vérifiant, et à un ensemble d'entiers naturels E la propriété d'appartenance associée, n ∈ E. La récurrence se réénonce alors de façon équivalente ainsi :

Soit E un sous-ensemble de N, si :

* 0 ∈ E
* n ∈ E ⇒ n+1 ∈ E (pour tout n ∈ N)

Alors E = N.

Bien sûr, l'initialisation peut commencer à un entier k arbitraire et dans ce cas la propriété n'est démontrée vraie qu'à partir du rang k :

Si :

* P(k) ;
* Pour tout entier n≥ k, [P(n) ⇒ P(n+1)] ;

Alors pour tout entier n≥ k, P(n).

Cette récurrence à partir de k est une conséquence immédiate de la récurrence à partir de 0 : il suffit de démontrer « n < k ou P(n) », ou encore « P(n+k) » si l'on dispose de l'addition, par récurrence sur n ; chacune de ces propriétés est bien vraie pour tout entier n si et seulement si la propriété P est vraie pour tout entier supérieur ou égal à k.

De façon analogue on aura d'autres raisonnements par récurrence, sans avoir besoin de poser à chaque fois un nouveau principe, par exemple, une récurrence sur les entiers pairs (prendre P(2n)), etc.

D'après Wiki ...


La Récurrence d'ordre 2

Il peut arriver que, pour l'hérédité, quand il s'agit de démontrer P(n + 1), on ait besoin de supposer la propriété aux deux rangs précédents, c'est à dire non seulement pour n, mais aussi pour n -1. On est amené à utiliser le principe de récurrence suivant :

Soit P(n) une propriété définie sur N, si :

* P(0)
* P(1)
* [P(n) et P(n+1)] ⇒ P(n+2) (pour tout n ∈ N)

alors P(n) pour tout n ∈ N.

Cette propriété est en apparence plus forte que la récurrence simple, puisque l'on a une hypothèse supplémentaire à notre disposition, mais lui est en fait équivalente, puisque cela revient à démontrer [P(n) et P(n+1)] par récurrence simple. On trouvera par exemple dans l'article suite de Fibonacci des exemples d'application de ce principe de récurrence.

On peut bien entendu généraliser à 3, 4 etc. Mais tous ces principes apparaissent comme des cas particuliers du principe de récurrence suivant, parfois appelé récurrence forte.

D'après Wiki ...

[mx6]

Pourquoi ne pas déduire la 5 de la 4 ??

[invite693d963c]

Ca ne serait pas une démonstration par récurrence

[A voir en vidéo sur Futura]

[mx6]

Ok je viens de le faire sur ma feuille, ce n'est pas si dur que ça n'a l'air
Par exemple en remplacer dans le premier terme de l'inégalité n par n+1, on a :
Ceci est plus grand que , mais on a un - avant, donc c'est vrai !
Par exemple si y-6 <x automatiquement y-9< x vu que 9>6

[invite693d963c]

Ok je viens de le faire sur ma feuille, ce n'est pas si dur que ça n'a l'air
Par exemple en remplacer dans le premier terme de l'inégalité n par n+1, on a :
Ceci est plus grand que , mais on a un - avant, donc c'est vrai !
Par exemple si y-6 <x automatiquement y-9< x vu que 9>6

Donc ...
- J'ai verifié pour n=1 et cela marche
- Ensuite Je fixe un rang no pour mettre en place mon hypothèse de reccurence
- Donc on dit que si Pno est vrai alors Pno+1 est vrai aussi :
Dans ce cas je remplace no par no+1 dans l'expression pour arriver à
J'en déduis que :
>
Soit :
>

Sachant qu'en remplacant no par no+1 je retrouve l'expression
Je conclus que P1 est vrai, Pno est vrai => Pno+1 est vrai => Pn est Tj vraie

Cela est correct ?
( Mhhhh quand Tu passe de à : Est ce que ce passage à un nom (propriété) ou est ce un axiome ? )

[mx6]

la fonction -x est décroissant dans R, donc c'est pour cela que le signe de l'inégalité change

[invite693d963c]

la fonction -x est décroissant dans R, donc c'est pour cela que le signe de l'inégalité change

En Faite, On peut faire l'analogie avec ( par exemple) :

7 > 4 > -4 <=> 7 > -4

[invite693d963c]

Pour la Question 6 a :

Pour Démontrer L'irrationalité du nombre e, Dois je prendre l'encadrement trouvé precedent en prenant une valeur de fixé ?

[invite693d963c]

Pour la Question 6 a :

Pour Démontrer L'irrationalité du nombre e, Dois je prendre l'encadrement trouvé precedent en prenant une valeur de fixé ?

L'encadrement de e par deux entiers rationnels consécutif permet il de montrer que e est bien irrationnel ?