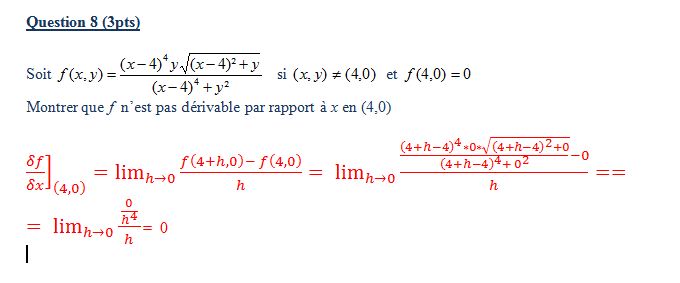Aide fonction censée être non dérivable en un point

[invite3999c982]

Bonjour,


Voici mon énoncé et ma réponse :




Ou se situe l'erreur ?
-----

[invite3999c982]

Vraiment besoin d'aide :s

[invite3df497c3]

euh... je ne suis pas certaine, mais je n'aurai pas procédé ainsi :
j'aurai plutôt cherché à montrer que la dérivée partielle de f par rapport à x n'est pas continue en le point (4,0), c'est-à-dire que j'aurai calculé df/dx et ensuite j'aurai exhibé deux suites qui tendent vers (4, 0) mais dont les images par df/dx sont différentes...

[invite3999c982]

mais d'apres les exercices du cours, moi je dois faire par ce systeme :s

[A voir en vidéo sur Futura]

[inviteea8ef274]

Bonjour,


Voici mon énoncé et ma réponse :




Ou se situe l'erreur ?

Je pense que vous avez commis une faute dans le début:

[invite3ba0dddb]

salut,
ta dernière limite c'est une forme indéterminé: 0/0
de plus on est pas censé faire la limite droite/gauche et voir une différence?

[invite3999c982]

salut,
ta dernière limite c'est une forme indéterminé: 0/0
de plus on est pas censé faire la limite droite/gauche et voir une différence?

Si mais je ne sais pas comment faire dans ce cas là

[invite93e0873f]

Je pense que vous avez commis une faute dans le début:

Non, le h n'est que dans l'argument en x, puisqu'on fait la dérivée partielle par rapport à x.

ta dernière limite c'est une forme indéterminé: 0/0
de plus on est pas censé faire la limite droite/gauche et voir une différence?

Je ne suis pas sûr qu'il s'agisse vraiment d'une forme indéterminée étant donné que peu importe h, dès que y vaut 0, la pente de la droite joignant (4,0,0) à (4+h,0, f(4+h,0)) est nulle (pour h non nul c'est sûr, donc à la limite ce l'est aussi). De plus, on voit que le numérateur est plus petit que le dénominateur pour x tendant vers 4 et y tendant vers 0.

Bref, je pense qu'il faut voir ça comme malix a dit. La fonction forme une surface continue sauf possiblement en (x,y) = (4,0) (on veut démontrer le 'sauf') au-dessus du plan Oxy. Montrer que la dérivée de f(x,y) existe en (4,0), c'est dire que la fonction est continue en ce point, soit que la limite existe (cette phrase est une tautologie ma foi!). Cela est possible uniquement si toute droite de Oxy passant par (4,0) voit l'image de ses éléments par f'_x converger vers une valeur indépendante du chemin quand on considère des points du chemin de plus en plus près de (4,0). Si deux chemins donnent deux résultats différents, alors la fonction dérivée en x de f(x,y) n'est pas continue en ce point, donc la dérivée de f(x,y) est ce point n'existe pas.

À date, on a vu que le chemin pour lequel y=0 donnait à f'_x(4,0) la valeur 0. Il faut voir si d'autres chemins donneraient le même résultat.

* Si cette limite existe.

[invite93e0873f]

Il faut voir si d'autres chemins donneraient le même résultat..

En fait, il faut voir si d'autres chemins ne donnent pas le même résultat, car on pourrait trouver 30 000 chemins différents donnant le même résultat, 30 000 sur une infinité, ce n'est pas une preuve. Par contre, un seul contre-exemple suffit (c'est un peu comme la réfutabilité des théories des sciences expérimentales; Popper n'est pas loin! (dans ma tête...)). Si après tant d'essais (de chemins) différents, tu obtiens toujours 0, il faudrait démontrer d'une autre façon que ce n'est pas égale à 0 (chose qui peut-être difficile...). Une façon que je vois c'est peut-être par la définition de la continuité, mais je ne sais pas si tu as déjà vu ça pour que ce soit une démarche justifiée.

Autrement, s'il y a une erreur dans ton calcul, à part l'histoire de forme indéterminée qui ne me semble pas s'appliquer ici, elle passe complètement inaperçue à mes yeux jusqu'à présent.

[invite93e0873f]

Sinon, il y a toujours KerLannais qui a réalisé dans ce fil-ci que tu as recopié sur le forum mathématiques du supérieur que ta fonction n'est pas définie si (x-4)²+y <0. Cela est donc parfait et explique pourquoi ce n'est pas différentiable (et qui de fait donne aussi partiellement raison à lawliet yagami pour l'histoire de limite à droite/à gauche) ; tous les chemins qui arrivent vers (4,0) en provenance de la zone où l'inégalité ci-haute tient ne peuvent donner de résultat. En effet, le point (4,0) donnant (x-4)²+y=0, soit la courbe représentant la frontière du domaine de définition de f(x,y), il n'est pas possible de dériver la fonction en ce point à cause de ça.

Ok, je m'exprime mal, tout ça serait mieux avec un dessin (que vous pouvez voir sur internet avec wolfram alpha j'imagine), mais la subtilité du problème réside uniquement dans le domaine de définition de f(x,y) et du fait que les points à la frontière du domaine de f(x,y) ne font pas partie (pour les raisons mentionnées) du domaine de définition de f'_x(x,y).