Calcul de limite en plus l'infini avec une racine
Discussions similaires
-
Par invite3f08773a dans le forum Mathématiques du collège et du lycée
Réponses: 15
Dernier message: 06/01/2009, 17h19
-
Par invite319fe712 dans le forum Mathématiques du collège et du lycée
Réponses: 4
Dernier message: 02/11/2008, 13h59
-
Par invite323995a2 dans le forum Mathématiques du collège et du lycée
Réponses: 3
Dernier message: 02/11/2008, 13h47
-
Par inviteae48fe17 dans le forum Mathématiques du collège et du lycée
Réponses: 2
Dernier message: 19/09/2007, 19h44
-
Par invite8ef93ceb dans le forum Mathématiques du supérieur
Réponses: 11
Dernier message: 28/11/2005, 22h58




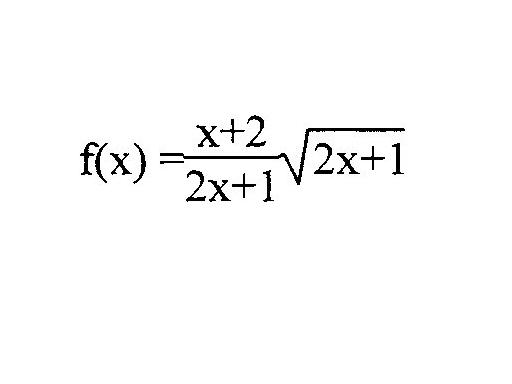

 l'expression conjugué est alors
l'expression conjugué est alors 

