Bonjour,
Me voilà avec un exercice (assez long) que j'ai du mal à résoudre. Je demande donc votre aide ^^
A) Etude d'une fonction numérique
f est la fonction définie sur ]1; +[ par f(x) = \frac{x^4}{x^2-1}. On appelle C sa courbe représentative dans un repère orthogonal (O, , ) ; unités : 4cm en abscisse et 0.5 en ordonnée.
1°) a. Vérifier que pour tout x de ]1;+ [, f(x) = x²+1+\frac{1}{x^2-1}
b. Etudier les limites en 1 et en +
2°) Soit P la courbe représentative dans le repère précédent de la fonction g définie sur ]1;+ [ par g(x) = x²+1
a. Quelle est la limite de f(x)-g(x) quand x tend vers + ?
b. Etudier la position de la courbe C par rapport à la courbe P ?
3°) Calculer la dérivée de f et étudier les variations de f.
4°) Représenter P et C
B) Volume du cône :
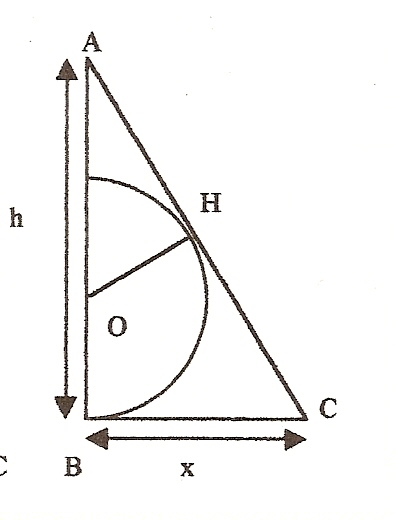
Dans la figure ci-contre : le triangle ABC est rectangle en B, le demi-cercle de centre O a pour rayon 1, la droite (BC) est tangente en B au demi-cercle, la droite (AC) est tangente en H au demi-cercle. On pose AB=h, BC=x (avec x>1).
1°) a. Prouver que \frac{OH}{AH} = \frac{BC}{AB}.
b. En déduire les égalités : h = x(h-1)²-1 ; x² = \frac{h}{h-2} ; h = \frac{2x^2}{x^2-1}
2°) On rappelle que le volume d'un cône de révolution de hauteur h et de base circulaire d'aire S est V = \frac{hS}{3}. En pivotant autour de (AB), le triangle ABC engendre un cône de révolution de sommet A.
a. Exprimer le volume V(x) du cône en fonction de x.
b. A l'aide des résultats de la partie A), déterminer pour quelle valeur de x le volume est minimum.
Calculer, pour cette valeur de x, l'angle  (à 0.1° près)
J'ai déja fait la partie A et je n'arrive pas à faire la partie B
-----