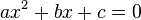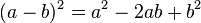Bonjour, je suis actuellement en 3éme et je fais en ce moment les x ainsi que les identités remarquables.
J'ai assimilés la factorisation&dévollepement.
Mais pourrais-je avoir de l'aide sur ces calculs ?
Merci.
Alors =>
A = x²-10x+25.
B = (x - 3)²
Bonsoir.
A) tu reconnais a²-2ab+b² que tu peux factoriser
B) (a-b)² à développer, non ?
EDIT : le fait que ce soit "x" ou "a" ou "patate" ne change rien au développement ou à la factorisation
Je vois pas pour le a.
b =>
x²-9 ??
Bonjour
A:
c'est une égalité de la forme
on nomme x1 et x2 les deux solutions.
(ici a=1, b=-10, c=25)
Si le discriminant est strictement positif, l'équation admet deux solutions x1 et x2 données par les formules suivantes :
Si le discriminant est été nul, l'équation admet une racine double :
et si le discriminant est strictement négatif, l'équation n'admet pas de solution réelle.
le discriminant ici est nul
donc la solution est
x= -(-10)/(2x1)= 5
pour le B, tu développe et tu fait la même méthode... à toi de jouer ! (fait le et on te confirmera la bonne réponse)
j'ai un doute... tu cherche x ou tu cherche à développer et factoriser?
car je vient de m'apercevoir que tes équation ne sont pas =0
je suis en troisiéme.
Je cherche le résultat, pas "x" =D
si c'est pour factoriser, pour le A tu suis cette règle:
avec a=1x et b=5
tu comprends?
et pour la B tu fait la même chose dans l'autre sens
A = x²-10x+25
A = 1² - ? + 5 ²
--' Je ne comprend pas.
non tu n'as pas vu mon a=1X et non 1
ça fait
A= 1x² -(2)(x)(5) + 5² = 1x²-10x+25
1x² - ? + 5² ?
Sans lire ton message j'ai 2 de justes.
J'ai toujour pas compris comment calculer le millieu du calcul.
exact j'avais oublié la fin du calcul:
ton "1x²-10x+25 " est de la forme(partie à droite= ) avec a=1x et b=5
si tu veux factoriser, tu applique la partie de gauche et tu trouve
A= 1x² -(2)(x)(5) + 5² = ( 2 - 5)² ... c'est ça la solution
(quand il n'y a rien entre deux parentèses, c'est comme un "multuplié")
A = (x-3)²
A = x²-6x+9
Alors C'est Bon Sa ?
dans mon message juste au dessus je me suis trompé, la solution est pas ( 2 - 5)² mais ( x - 5)²
et oui pour ton B=x²-6x+9
Bonjour.
J'avais quasiment tout dit pourtant
Il suffit d'écrire x² -10x + 25 sous la forme a² - 2*a*b + b²
x² - 10x + 25 = x² - 2*5*x + 5² = (x-5)²
Duke.
D'accord, le b est juste ?Envoyé par Duke Alchemist
Bonjour.
J'avais quasiment tout dit pourtant
Il suffit d'écrire x² -10x + 25 sous la forme a² - 2*a*b + b²
x² - 10x + 25 = x² - 2*5*x + 5² = (x-5)²
Duke.
Comme te l'a dit shtroumpf sensé...
"sans c" ?!... ha ha ha... jdm tout pourri
c'est bien ça.
Lis-tu bien les réponses que l'on te fait ?
EDIT : Pour le B, c'est le procédé inverse de mon message précédent
