Exercice de math de 1ere S

[magicienbang]

Bonjour,

voila, je bloque sur un exercice de math, je n'arrive pas à me débloquer, c'est pourquoi je préfère demander l'avis d'autre personnes. je vous donne l'ennoncé puis je vous dirait ou j'en suis et les démarches que j'ai essayé . en ésperant que vous pourrez éclairer ma lanterne .... voici le sujet :

énoncé :

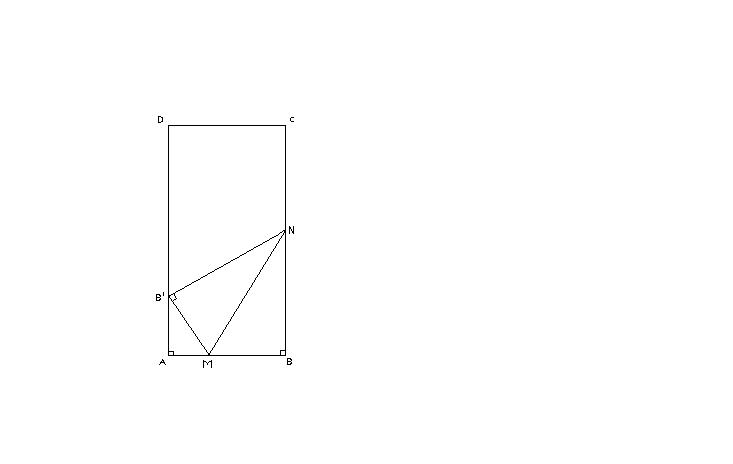
On dispose d'une feuille de papier rectangulaire ABCD telle que :
AB= 1dm
AD= 2dm
On plie cette feuille de façon à amener le point B en un point B' de [AD], de sorte que la partie pliée soit triangulaire.
La feuille est pliée suivant la droite (MN) ou M appartient à [AB] et N appartient à [BC].
On pose :
a=AB'
b=BN


1) a) Exprimer AM et BM en fonction de "a".

à cet exercice j'ai utilisé le théoreme de pythagore,
comme AMB' est un triangle rectangle en A:

B'M² = AB'² +AM²
B'M² = a² + AM²
mais comme B'M = BM et que BM = 1-AM :

(1-AM)² -AM² -a² = 0
(1 - 2AM + AM²) - a² - AM² = 0
1 - 2AM - a² = 0
AM = (1-a²)/2

j'ai suivi le meme plan pour trouver BM = (1+a²)/2

b) En calculant de deux manières différentes l'aire du trapèze ABNB', démontrer que b=(1+a²)/2a

sur celui-la je vois bien qu'il est possible d'additionner l'aire des triangles AMB' ; MBN ; MNB' . cependant je ne vois pas quelle est l'autre méthode ... pourriez vous m'aider ?
-----

[invite0b269ea8]

aire trapèze = hauteur*(grande base + petite base)/2

Soit ici : aire = 1*(a+b)/2 = (a+b)/2 = autre formule avec les 3 triangles
En simplifiant tu trouves ce qu'il faut.

[magicienbang]

Merci ! donc je calcule :

(a+b)/2 = somme des Aires des triangles
(a+b)/2 = [a((1-a²)/2)]/2 + b[(1+a²)/2]
(a+b)/2 = [a(1-a²)]/4 + (b+ba²)/2
a+b = [a(1-a²)]/2 + b+ba²
a-ba² = [a-(a^3)]/2
-ba² = [a-(a^3)-2a]/2
b = [a+(a^3)]/(2a²)
b = (1+a²)/2a

C) En déduire que a appartient à l'intervalle [2-racine(3) ; 1]

sur cet exercice, je ne vois absolument pas comment faire .
pourriez vous me donner une piste ?

[invite0b269ea8]

A partir b=(1+a²)/2a, exprime a en fonction de b (passe le 2a à gauche puis équation du 2° degré ; deux solutions mais une seule est géométriquement possible) et calcule a pour b=0 puis b=2 (positions extrêmes du point de contrôle N).

[A voir en vidéo sur Futura]

[magicienbang]

interessant,

donc :

2ba - a² - 1 = 0

c'est bien un polynome, mais je ne vois pas comme il peut m'aider...

[magicienbang]

ah d'accord, je remplace , dans ce polynome, b par ses extreme, désolé je n'avais pas compris^^ :

b=2 :

-a²+4a-1 = 0
delta = 12

solution 1 : 2+ racine(3)
solution 2 : 2-racine(3)

j'ai bien trouver 2-racine(3) mais pourquoi puis-je dire que l'autre n'est pas possible ? et comment trouver 1 comme maximum ?

[invite0b269ea8]

2+racine(3) mettrait B' au dessus de D
a=1 correspond à M=A
(Les 2 situations sont les cas limites de la configuration "pli en triangle qui recouvre la feuille")

[magicienbang]

merci, effectivement, c'est simple et logique, je n'y avait pas asser reflechis ^^"

2) On designe par S la mesure en dm² de l'aire de la partie pliée.
a)Démontrer que S=(1/8) * g(a)

sur celui-la j'ai procédé ainsi :

S= ([b]*[(1+a²)/2])/2
= ([(1+a²)/2a]*[(1+a²)/2])/2
= [(1+a²)/4a] * [(1+a²)/4]
= (1+a²)²/16a
= (1/8) * [(1+a²)²/2a]

cela vous semble-t-il juste ?

[invite0b269ea8]

Il me semble que c'est plutot 1/8 * (1+a²)²/a (pas de facteur 2 en bas)
Mais à vérifier ^^
Sinon dans l'idée c'est ça

[magicienbang]

apres verification, je trouve bien S = 1/8 * (1a²)²/2a ,
car S= (1+a²)²/16a
= (1+a²)²/(2a*8)
sauf si j'ai raté mon calcul depuis le debut, sans que je vois l'erreur, cela me parait juste ^^

b) En déduire la valeur de a pour laquelle S est minimale et calculer ce minimum.

pour celui-la, j'ai opter pour la derivation, ne voyant pas de methode plus rapide :

g(a) = (1+a²)²/2a = U/V

U= (1+a²)² U' = 2(a²+1)
V= 2a V' = 2

g'(a) = [U'V-UV']/V²
= ( [ 2*2a*(a²+1)] - [2*(a²+1)²] ) / 4a²
= [ 4a(a²+1) - 2(a²+1)² ]/4a²
= [ 2a(a²+1) - (a²+1)² ] /2a²
= [ (a²+1) ( 2a - (a²+1) ) ]/2a²
= [ (a²+1) (-a² + 2a - 1 ) ]/2a²
= [ (a²+1) [ -1*(a-1)²] ]/2a²

avant de commencer le tableau de variation, est-ce correct ?

[invite0b269ea8]

g'(a) = (1+a²)(3a²-1)/2a²

[magicienbang]

euh, je suis désolé mais je ne comprend pas comment tu as trouver ce resultat ^^", pourrais tu m'expliquer ?

[invite0b269ea8]

En fait quand tu fais u(a)=(1+a²)², tu ne peux pas écrire u'(a) = 2(1+a²), parce que tu dérives par rapport à la variable a et non par rapport à ce qui est dans le carré (ici c'est l'expression 1+a²). Tu verras une règle l'an prochain pour traiter ça, en attendant il faut développer :
u(a) = 1 + 2a² + a^4 et dériver terme à terme (ici tu peux appliquer les règles sur les puissances, car ce sont des puissances de a, variable de ta fonction u).
Après calcul ca fait : u'(a) = 2*(1+a²)*2a (en refactorisant)
et en bricolant (u'v-uv')/v² tu obtiens ce que je t'ai écrit

[magicienbang]

ah d'accord ! ^^ merci

bon alors, apres tableau de variation, la valeur de a pour laquelle S est minimum est 1/(racine{3])

3) a) Démontrer que L=1/2 * racine [ f(1/a²)]

bon alors, la je réutilise pythagore :

L² = BM² + BN²
L² = [(a²+1)/2]² + [(a²+1)/2a]²
L² = [(a²+1)²/4 ] + [( a²+1)²/4a²]
L² = [ a²(a²+1)² + (a²+1)²] /4a²
L² = [(a²+1)²(a²+1)]/4a²
L² = [(a²+1)^3]/4a²
L² = (1/4) * [(a²+1)^3]/a²
L = 1/2 * racine ( [(a²+1)^3]/a² )

voila, le seul problème, c'est qu'a partir de la, je bloque ...
je ne sait pas quoi faire, pouvez vous m'aider ?