Une equation différentielle qui ne vérifie pas toutes les solutions...

[Moonset]

Bonjour,

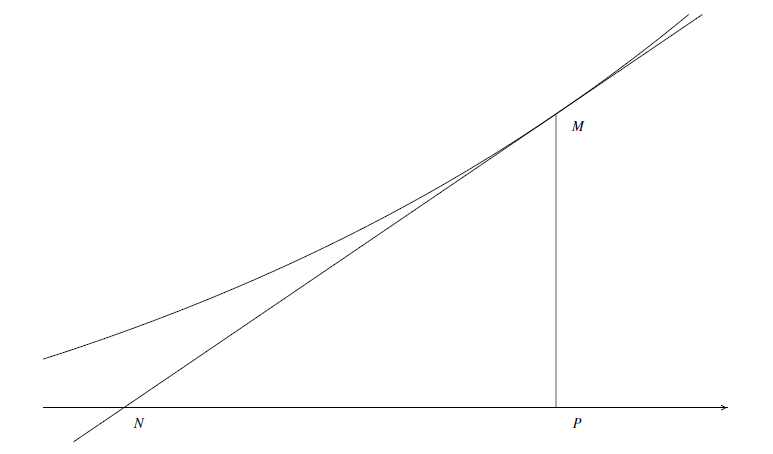
Je suis sur un exercice où f désigne une fonction strictement positive et strictement croissante. On a M un point de la courbe, d'abscisse t , P un point d'abscisse t et d'ordonnée 0. La tangente en M à la courbe coupe l'axe des abscisse en N. On cherche à étudier la distance PN.



Question 1 : on exprime PN en fonction de f (t) et f '(t).
Je répond :

 Cliquez pour afficher

équation de la tangente : y = f '(t) (x - t) + f (t).
Or, N appartient à la tangente et à l'axe des abscisse donc 0 = f '(t) ( Xn - t) + f (t). Après quelques péripéties,
Xn = [ t f ' (t) - f (t) ] / [ f ' (t) ]

Ensuite, comme je ne voulais pas me trimbaler avec des racines carrées ou des valeures absolues, j'ai écris quelque chose dont je ne suis pas sur de l'exactitude :
Tn a un coefficient positif
Pour tout x , f ( x ) est positif
Donc Xn < Xp
De plus, N et P alignés et appartiennent à l'axe des abscisses.
Donc NP = Xp - Xn = t - Xn = péripéties

= - f(t)/f '(t) = PN

Question 2 : Etablir une équation différentielle vérifiée par les fonctions telles que PN = constante
Je répond :
- f (t) / f '(t) = k
f '(t) = (-1/k) f (t)

Question 3 : On résout cette équation.
Donc je répond :
f ( t ) = C * exp ( -t/k )
Or f ( t ) > 0 donc C > 0
Seulement, je trouve que ça n'a pas vraiment de sens. Les fonctions du type f ( t ) = exp ( t/k ) marchent aussi, et elles ne sont pourtant pas dans mon ensemble solution. De plus, l'énoncé stipulait f strictement croissante, ce qui n'est pas le cas des fonctions de mon ensemble solution.

Où est mon erreur s'il vous plaît ? Merci d'avance.

[RoBeRTo-BeNDeR]

Bonjour,

f est strictement positive et croissante, donc comme PN=-f/f' alors PN<0 ce qui est impossible si on parle d'une distance...

[Moonset]

Oui ça m'avait choqué aussi mais pourtant je n'arrive pas à tomber sur autre chose par le calcul.

[Gagaetan]

Salut

Moi je tombe sur PN=f/f'

Avec f(t)=Ke^(t/c)

Tu as du te tromper a la premiere question

[Gagaetan]

PS : il y a beaucoup une méthode plus rapide et plus simple pour résoudre la 1ere question