Bonjour
Pourriez vous m'apporter votre aide pour réussir mon exercice s'il vous plait
Voici l'énoncé:
Soit g la fonction définie par g(x)= 1/(x+1), x appartient à ]-1;0[
g(x)= cos(x), x strictement sup ou égal à 0
a) g est-elle continue en 0?
b) g est-elle dérivable en 0?
c) Expliquer ce qu'il se passe au voisinage de 0
Voila mes réponses:
a) La fonction cos est continue sur R donc continue en 0 à droite
lim 1/(x+1)= 1
x-->0-
g est continue en zéro à gauche
g est donc continue en 0
b) g est dérivable en 0 car g est défini et continue en 0
c) Au voisinage de 0 ...???
Pourriez vous me corriger
Merci d'avance
-----





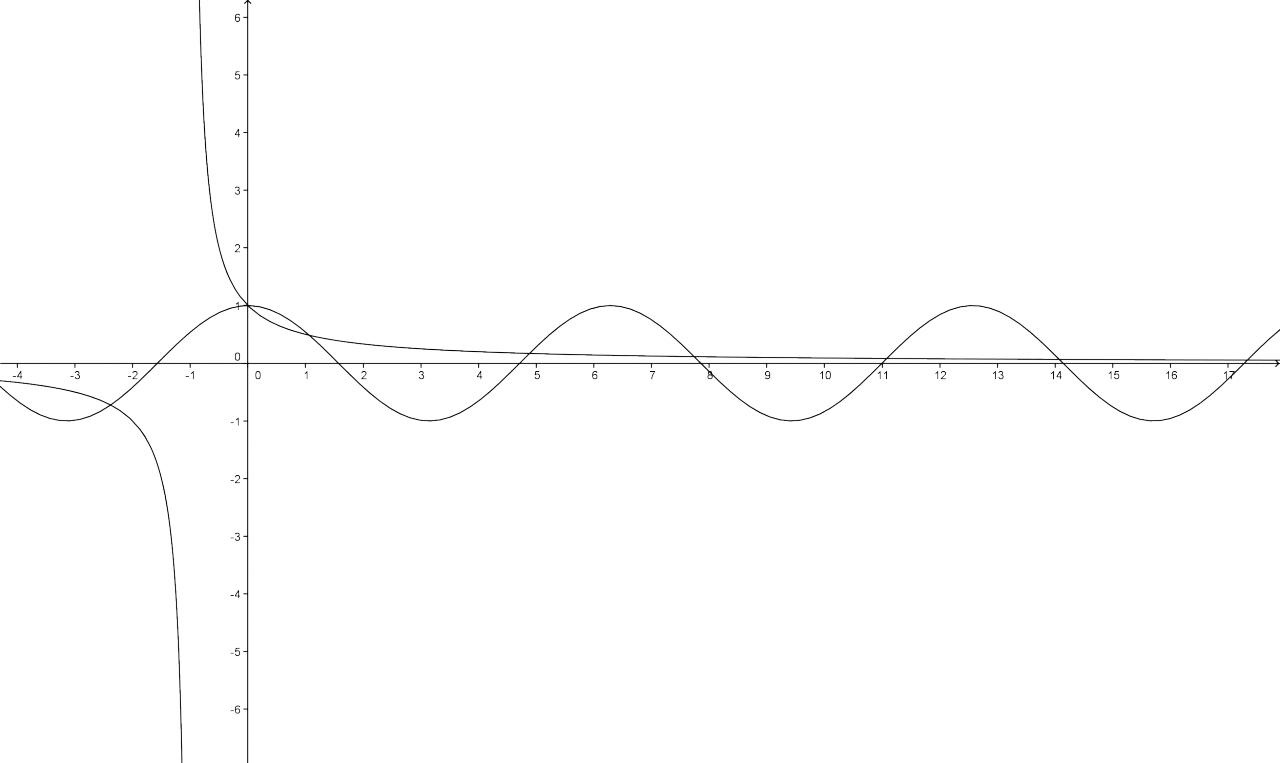


 donc continue à gauche. Et à droite la fonction cosinus est continue, donc c'est continue
donc continue à gauche. Et à droite la fonction cosinus est continue, donc c'est continue