Fonction composé d'une aire d'un triangle en fct de x

[inviteffa1ebb5]

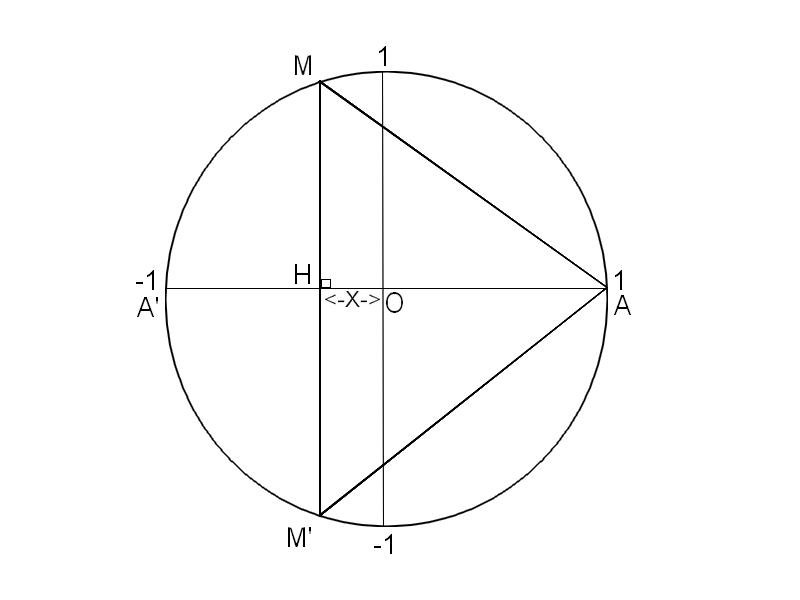
Bonjour, j'ai un exercice de maths dans un dm, (qui est le 6 p141 dans les annales ABC Nathans 2011 pour ceux qui connaissent) et dans lequels on me demande d'exprimer la valeur de l'aire du triangle MAM' en fonction de x.

Je choisi donc d'utiliser une fonction composée définissant l'aire de ce triangle tels que : A(x)=g(x)*h(x)




-Soit la fonction g(x) définissant la distance HA :

g(x) = OA-OH
g(x) = 1-x

-Soit la fonction h(x) définnissant la distance HM :
MAH étant un triangle rectangle en H, alors d'après le théorème de pythagore : (MH)^2 +(HA)^2 = (MA)^2
donc : (HM)^2 = (MA)^2 - (HA)^2

h(x) = HM = racine( MA^2 - HA^2)
= racine( MA^2 - (g(x))^2)
= racine( MA^2 - (1-x)^2)
= racine( ((g(x)/sin(90))^2 - (1-x)^2) --> car sin(MHA) = HA/MA
= racine( ((1-x)/sin(90))^2 - (1-x)^2) sin(90) = g(x)/MA
= racine( (1-x)^2 - (1-x)^2) donc MA = g(x)/sin(90)
= racine( 0 )
h(x) = 0

Et c'est pas du tout ce que j'avais prévu !!!!!!

Puisque après avoir trouvé l'expression de h(x) j'en aurai conclus que :
A(x) = g(x)*h(x)
car l'aire du triangle MAH = HA*MH <=> g(x)*h(x)

Peut être que j'ai cherché trop compliqué, ou tout simplement que je me suis trompé dans mes calculs, mais svp aidez moi
-----

[invitec8d1794b]

(MH)^2 +(HA)^2 = (MA)^2
HM = sqrt(MA²) - sqrt(HA²)

Ca devrait mieux aller comme ça

[inviteffa1ebb5]

je veux bien si tu le dis, mais ca veux dire quoi "sqrt" ?

[inviteffa1ebb5]

J'ai trouvé, ca veut dire racine carré, merci à toi, je vois ce que ça donne maintenant.

[A voir en vidéo sur Futura]

[inviteffa1ebb5]

(MH)^2 +(HA)^2 = (MA)^2
HM = sqrt(MA²) - sqrt(HA²)

Ca devrait mieux aller comme ça

Merci de m'avoir répondu, mais excuse moi par ce que je ne vois pas bien ce que ça change puisque je trouve toujours :

h(x) = sqrt( ((1-x)/(sin(90)))^2 ) - sqrt ( (1-x)^2 )
= (1-x)/(sin90) - (1-x)
et comme sin(90) = 1 ->cercle trigonométrique, alors :
= (1-x) - (1-x)
h(x) = 0

[invite427a7819]

Pour a et b réels, a² > b², ... L'expression de droite est définie pour tout a et b réels, et pas celle de gauche... On doit pouvoir rapidement trouver un contre exemple.

Le problème arrive quand tu remplaces par , parce que sin(90), c'est 1... Ton triangle étant rectangle en H, tu as sin(HAM) = HM / AM et sin(HMA) = HA / AM. Il est impossible (et parfaitement inutile) d'exprimer le sinus ou le cosinus de l'angle droit du triangle.

(Et en passant, ta fonction n'est pas une composée mais un produit. La composée s'écrit f(g(x)), et ce n'est pas le calcul que tu fais ici).

[inviteffa1ebb5]

D'accord, je cherchais à exprimer HM en fct de cet angle car il garde une valeur constante mais effectivement ça ne peut pas marcher. Même avec la tangente ça ne donne rien. J'abandonne donc l'idée d'utiliser pythagore.

Si on place sur le cercle "cos" entre O et A, et "sin" entre O et 1 (celui du haut), j'ai trouvé h(x) = sin(x) avec la fonction h définie sur [-1;1].

Ca me donnerai donc pour l'aire du grand triangle :
A(x) = g(x)*h(x)
= (1-x)(sin(x))
= sin(x)*-x*sin(x)
A(x) = -x*sin²(x)

Par contre ça ne donne pas une fonction ayant une expression graphique de forme "n" ,mais une fonction décroissante et négative sur l'interval ]0;1].
Salut,

[invite427a7819]

Ta dernière ligne est fausse, de A(x) = sin(x) - x*sin(x), on ne peut pas déduire A(x) = -x*sin(x)².

De plus, d'après ton schéma, x représente l'abscisse du point H, et est donc (dans le cas que tu nous propose) négatif... Ou alors, c'est g(x) qui est incorrectement défini et vaudrait (1+x). Enfin, tu fais une confusion, un point du cercle unitaire a pour coordonnées (cos(x);sin(x)) et pas (x;sin(x)).

Pour moi, pythagore est une bonne piste, mais je l'appliquerais plutôt dans le triangle MHO que le triangle MAH.

[inviteea028771]

Non, la hauteur n'est pas égale à sin(x). Ici tu as cos(a) = x et h(x) = sin(a) (avec a l'angle AOM)

or cos²(a)+sin²(a) = 1, donc x² + h²(x) = 1, d'où h(x) = racine(1-x²) (on prend h positive)

[invite80e0db49]

Il y a bien plus simple pour traiter de ton sujet, je ne te donne pas le résultat mais des pistes.

Pense à une propriété de 3ème, sur les triangles semblables. En effet tu as AHM semblable à AON avec O le centre du cercle et N l'intersection entre [MA] et [Oy)

De plus tu sais que 1-N=x, et oui tu travaille dans un cercle ! Tu peux donc dire que MH/NO=AH/AO=AM/AN

Bon je ne simplifie pas plus pour te laisser un minimum chercher.

[ansset]

vous êtes tous très compliqué, sans compter quelques erreurs un peu grave ( Stolen....heart, c'est vilain d'ecrire
a²=b-c >= a=rac(b)-rac(c) :

bon revenons à AMM'
la surface d'un triangle S= hauteur*base/2

hauteur= HA = (1+x) et pas 1-x que j'ai vu passé aussi !
base =M'M= 2*HM
OM² = x²+HM² ( pythagore) et M est sur le cercle donc OM=1
donc base/2 = HM=rac(OM²-x²)=rac(1-x²)

d'ou S=(1+x)*rac(1-x²)

ps : j'avais pas vu le mess de Tryss

[ansset]

ps :
x est présenté ici comme une distance entre O et H. ( A'<-H->O )
mais ii x doit être considéré "négatif" si H entre O et A' et positif entre O et A
il faut changer son signe

[inviteffa1ebb5]

Pense à une propriété de 3ème, sur les triangles semblables. En effet tu as AHM semblable à AON avec O le centre du cercle et N l'intersection entre [MA] et [Oy)

De plus tu sais que 1-N=x, et oui tu travaille dans un cercle ! Tu peux donc dire que MH/NO=AH/AO=AM/AN

Oui, je vois bien que tu parle du théorème de thales, mais içi on n'a seulement connaissance des 2 distances AO=1 et AH=x et donc HA par conséquent. Il n'est donc pas applicable. Merci quand même.

[inviteffa1ebb5]

bon revenons à AMM'
la surface d'un triangle S= hauteur*base/2

hauteur= HA = (1+x) et pas 1-x que j'ai vu passé aussi !
base =M'M= 2*HM
OM² = x²+HM² ( pythagore) et M est sur le cercle donc OM=1
donc base/2 = HM=rac(OM²-x²)=rac(1-x²)

d'ou S=(1+x)*rac(1-x²)

C'est effectivement ce que je viens à peu près de trouver quand j'ai vu que on connaissait aussi la distance MO=1

merci à Elwyr pour

Pour moi, pythagore est une bonne piste, mais je l'appliquerais plutôt dans le triangle MHO que le triangle MAH.

---

Par contre contre Ansset je trouve :

Soit la fct h(x) [...] Sachant que le triangle HMO [...] alors : MO² = MH² + HO²
donc : MH² = MO² - HO²

h(x) = MH = rac((1)²-(x)²)
= rac(1-x²)

A(x) = g(x)*h(x)
= (1-x)*(rac(1-x²))
A(x) = rac(1-x²) - x(rac(1-x²))

Tu en pense quoi ?

ps : x est présenté ici comme une distance entre O et H. ( A'<-H->O )
mais ii x doit être considéré "négatif" si H entre O et A' et positif entre O et A
il faut changer son signe

Je ne vois pas pourquoi il faudrait inverser le signe puisque ça marche bien avec x négatif et positif. ??

[invite80e0db49]

Oui, je vois bien que tu parle du théorème de thales, mais içi on n'a seulement connaissance des 2 distances AO=1 et AH=x et donc HA par conséquent. Il n'est donc pas applicable. Merci quand même.

Non tu as connaissance d'autre distance vu que tu travailles dans un cercle je parle de NO

[ansset]

A(x) = g(x)*h(x)
= (1-x)*(rac(1-x²))
A(x) = rac(1-x²) - x(rac(1-x²))

Tu en pense quoi ?

Je ne vois pas pourquoi il faudrait inverser le signe puisque ça marche bien avec x négatif et positif. ??

pour la première question, c'est bon, juste une autre écriture.
pour la deuxième question
tout dépend de la définition de x
si x reste une distance positive de O vers A', il n'y a pas de raison de changer, à condition de pendre un x<0 si H est entre O et A.
ma remarque tient au fait que dans le dessin, on place A en +1 et A' en -1. Ce qui peut induire en erreur.

donc la démonstration est bonne à condition que l'on dise x = distance entre O et H avec x=1 pour H=A'

[ansset]

je corrige jutement un truc c'est = (1+x) *(rac(1-x²)) si H est placé comme sur le dessin avec x>0 dans ce cas de figure.
si c'est l'inverse ( voir précedent message )
avec x<0 si H entre A' et 0
et x>0 si H entre 0 et A alors c'est bien ( 1-x)...

[inviteffa1ebb5]

Merci, c'est ce que j'ai finalement trouvé aussi, et c'est le bon résultat.
Merci à vous