Bonjour j'ai besoin d'aide pour cet exercice s'il vous plait!
Une entreprise veut réaliser les deux montants latéraux d’un toboggan. La courbe
qui modélise le toboggan est définie comme une partie de la représentation graphique (C ) d’une fonction f dans un repère orthonormé adapté.
Question préliminaire
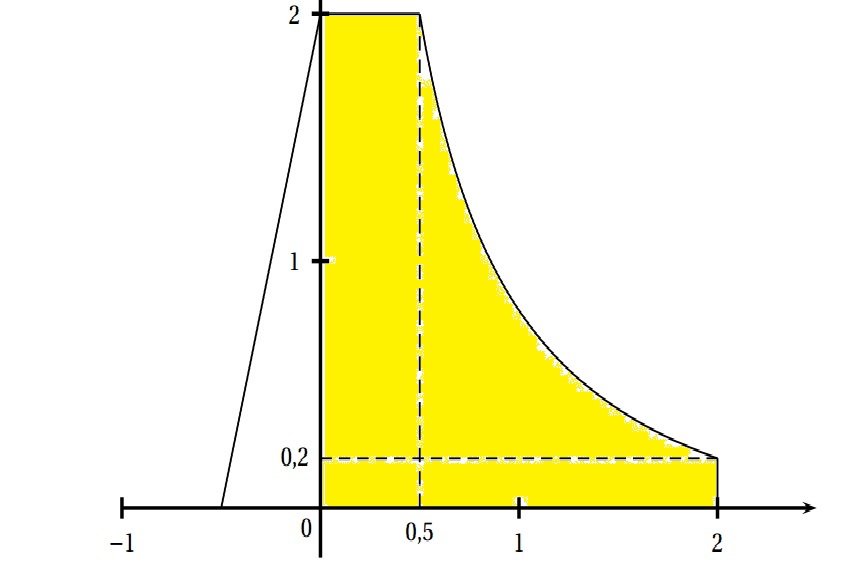
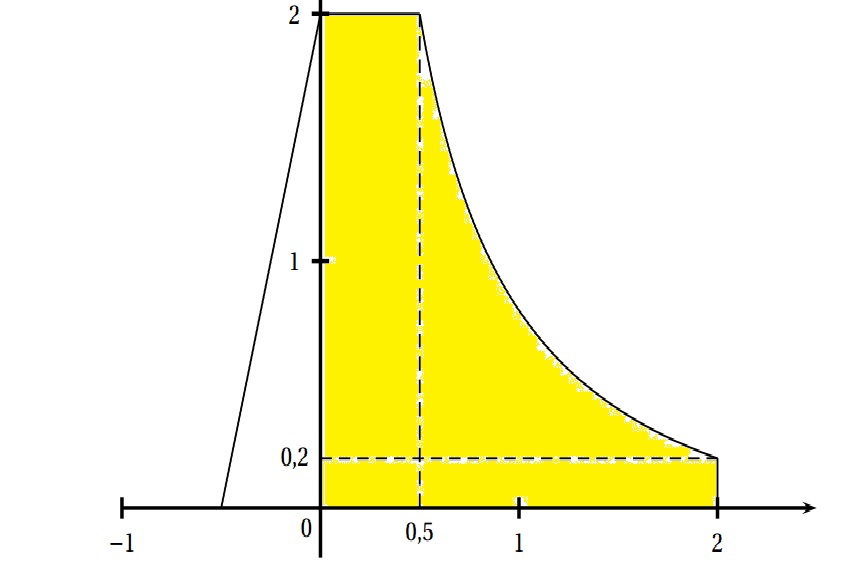
La partie utile de la courbe (C ) qui modélise le toboggan est délimitée par les points
de coordonnées (0,5 ; 2) et (2 ; 0,2) comme le suggère le schéma ci-dessus.
La fonction f est définie, pour tout nombre réel x strictement positif, par
f (x) = a +b/x
où a et b sont deux nombres réels.
Déterminer a et b.
Partie A. Étude de fonction
On admet que la fonction f est définie sur l’intervalle [0,5 ; 2] par :
f (x) = −0,4+1.2/x
.
On note (C ) sa courbe représentative dans un repère orthonormal(O,I,J)
1. On note f′
la fonction dérivée de la fonction f . Calculer f′(x) pour tout nombre réel x de l’intervalle [0,5 ; 2].
2. Étudier le sens le variation de la fonction f sur l’intervalle [0,5 ; 2].
3. Déterminer une équation de la tangente T1 à la courbe (C ) au point d’abscisse
0,5 et une équation de la tangente T2 à la courbe (C ) au point d’abscisse 2.
4. Tracer, dans le repère indiqué, les droites T1 et T2, ainsi que la courbe (C ).
5.Donner un encadrement de l'aire de la partie jaune du toboggan en utilisant d'une part les droites t1 et t2 et d'autre part le point de coordonnés(1;0.8)
J'ai réussi toutes les questions sauf la dernière
comment déterminer un encadrement à partir de deux droites et d'un point?
info T1 y=-4.8x+4.4 et T2 y=-0.3x+0.8
-----