Produit scalaire

[F-BVXT]

Bonjour,
Je suis en première S et j'ai un exercice à faire sur les produits scalaire mais je n'y arrive pas.

Enoncé :
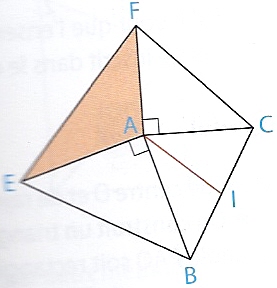
ABC est un triangle quelconque. On construit les triangles CAF et BAE rectangles isocèles en A. On veut prouver que la médiane (AI) du triangle ABC est une hauteur du triangle AEF.

1) Montrer que →(AB).→(AF)=→(AC).→(AE)
2) Exprimer →(AI) en fonction des vecteurs →(AB) et →(AC)
3) Prouver que →(AI).→(EF)=0

Pour la première question j'ai essayé en partant de →(AB).→(AF), puis de →(AC).→(AE) et même avec →(AB).→(AE)=→(AC).→(AF) mais je ne suis pas arrivé au résultat.
N'y arrivant pas je suis donc passé à la question 2 et j'ai mis →(AI)=→(AB)+→(BI)=→(AC)+→ (CI) mais je ne pense pas que ce soit ça qui est demandé parce que ça ne m'aide pas du tout pour la suite.

Toute aide est la bienvenue,
Merci d'avance.
-----

[Jon83]

Bonjour!

Déja, un bon dessin peut faciliter le raisonnement....Tu as Géogébra V4 qui est téléchargeable gratuitement et d'utilisation aisée!!!

[F-BVXT]

Voilà la figure, personnellement je l'avais dessiné à la main.

[Mpropre984]

J arrive à BC.(AF+AE)=0, et après je ne sais pas continuer, desolé.

[A voir en vidéo sur Futura]

[F-BVXT]

Est-ce que tu peux me dire comment tu es arrivé à ce résultat parce qu'après moi je sais continuer
Si je ne dis pas de bêtise avec les projetés orthogonaux ça donne :
→(BC).→(AF) + →(BC).→(AE)=0
→(AB).→(AF) + →(AC).→(AE)=0
→(AB).→(AF)= - →(AC).→(AE)

Il doit donc y avoir une erreur quelque part...

[sammy93]

Salut.
Tu peux utiliser la définition du produit scalaire:
et .
L'égalité est évidente si tu remarques que les angles EAC et BAF sont formés de deux angles égaux.
2°.Il suffit d'écrire .
Sauf erreur.

[F-BVXT]

D'accord merci beaucoup. Je n'avais pas pensé au fait que les angles BAF et EAC étaient égaux.

[stellouche]

Bonjour, j'ai le même exercice à faire et bien que je pense avoir réussi les questions 1 et 2 je bloque totalement sur la 3eme ..
Il faut sûrement utiliser le projeté orthogonal mais je ne comprends pas comment donc je ne sais pas prouver que AI.EF = 0
merci de votre aide

[ansset]

Salut.
Tu peux utiliser la définition du produit scalaire:
et .
L'égalité est évidente si tu remarques que les angles EAC et BAF sont formés de deux angles égaux.
2°.Il suffit d'écrire .
Sauf erreur.

En reprenant la prop de Sammy pour AI
En écrivant .
et en utilisant le resultat de la question 1)

[stellouche]

Merci pour votre aide donc si je comprends bien :

EA = BA et AF = AC donc
EF = BA + AC

On a trouvé AI = 1/2 AB + 1/2 AC

Donc AI.EF = (1/2 AB + 1/2 AC).(BA + AC)
= (1/2 AB + 1/2 AC).(-AB + AC)

???

[ansset]

non
"EF = BA + AC " ça sort d'où ça ?????
EF=EA+AF ! (en vecteur )
tu ne lis pas ?

[stellouche]

non je ne comprends pas trop où vous voulez en venir ..

[ansset]

De faire simplement le développement.
AI.EF en remplaçant
AI par (1/2)(AB+AC) et
EF par (EA + AF)
Et de tenir compte du résultat de la question 1)

tout ça en vecteurs bien sur

[stellouche]

je crois que j'ai trouvé, merci beaucoup

[leomath85]

Désolé mais je n'arrive pas à comprendre en quoi l'égalité est évidente (!)
Il y a quelque chose qui m'échappe. Est-il possible de détailler ? Merci!

Salut.
Tu peux utiliser la définition du produit scalaire:
et .
L'égalité est évidente si tu remarques que les angles EAC et BAF sont formés de deux angles égaux.
2°.Il suffit d'écrire .
Sauf erreur.

[topmath]

Bonjour :

Voila un bon rappelle Produit Scalaire .

Cordialement

[gg0]

Dans le deuxième produit scalaire, c'est bien sûr AC.AE.cos(EAC) ce qui fait que ce sont deux produits de trois nombres identiques d'un produit à l'autre.

Cordialement.