Quadrature du Cercle et valeur de Pi

[Guimzo]

Bonjour,



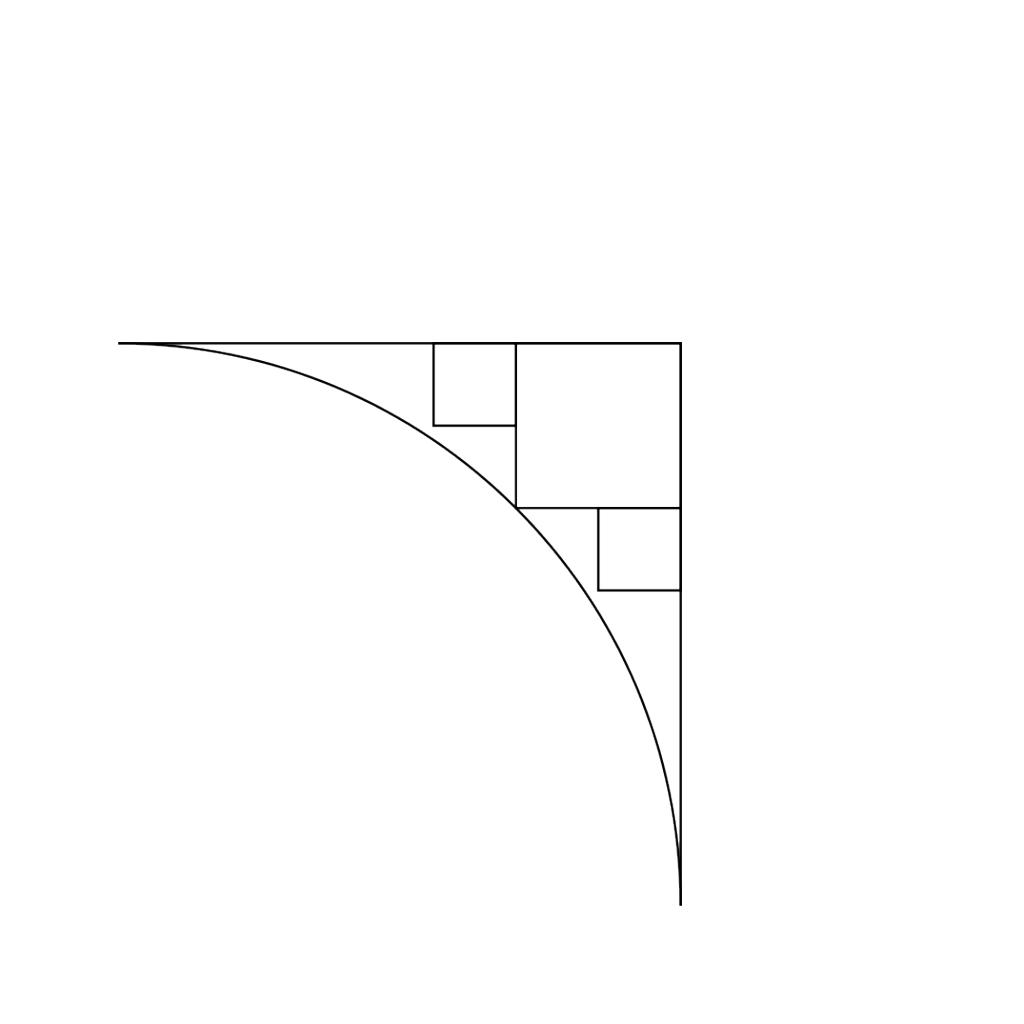
Il est joint à ce post un graphique expliquant une démarche qui consiste à trouver une raison mathématique
à une suite qui donnerait très propbablement la valeur de Pi.


C'est la somme de certains rapports de [ ( 3/2 ) - sqrt (2) ]

qui est le coefficient de l'aire du carré dont la diagonale est la différence entre la diagonale du carré de côté R, rayon d'un cercle, et le Rayon R lui-même.

Peut-on donc trouver une raison mathématique à la suite :


Pi =

2
+ 1
+ ( 1/1 ) * [ ( 3/2 ) - sqrt (2) ]
+ ( 1/2 ) * [ ( 3/2 ) - sqrt (2) ]
+( 1/8 ) * [ ( 3/2 ) - sqrt (2) ]
+( 1/64 ) * [ ( 3/2 ) - sqrt (2) ]
+( 1/128 ) * [ ( 3/2 ) - sqrt (2) ]
+( 1/512 ) * [ ( 3/2 ) - sqrt (2) ]
+( 1/8192 ) * [ ( 3/2 ) - sqrt (2) ]
+( 1/131072 ) * [ ( 3/2 ) - sqrt (2) ]
+( 1/262144) * [ ( 3/2 ) - sqrt (2) ]
+..............??


Comment formaliser cette suite peut-être avec un sigma.....??

[Duke Alchemist]

Bonsoir.

Alors là comme ça je ne vois pas directement la réponse... mais en fait, je suis plus intrigué sur l'origine de ces termes successifs...
Je n'arrive pas à faire le lien entre le dessin et l'expression trouvée...
Peut-être cela permettrait-il de trouver la solution ?

Cordialement,
Duke.

[tekmat]

Tu fais de toute façon fausse route, l'expression que tu cherche est de la forme:



Si tu compte déceler dans le développement une suite géométrique alors Pi est rationnel, si tu pense que c'est plusieurs suites géométriques, même résultat, si tu pense qu'on a la suite des puissances d'un demi privée de sous-suites géométriques c'est pareil, au final au mieux tu auras une suite chaotique sans raison.

Et dans ce cas ta recherche n'a aucun intérêt, des formules pour Pi il en existe comme:



Tu pars de 4 tu retire 4/3, tu remet 4/5, tu retire 4/7 et ainsi de suite, tu tourne autour de pi en t'approchant toujours plus. Connu en Inde au Vème siècle.

Quant à cette formule proposée j'ai l'impression que celui qui l'a écrit tente de paver la différence entre le carré et le quart de disque par des petits carrés qui sont d'aires proportionnelles au carré EFGH avec des facteurs 1/2^n sauf que ça ne peut fonctionner vu qu'ils ne collent pas au cercle:
Cercle.jpg

[Guimzo]

Bonjour tekmat,

Tu fais de toute façon fausse route, l'expression que tu cherche est de la forme:

Si tu compte déceler dans le développement une suite géométrique alors Pi est rationnel, si tu pense que c'est plusieurs suites géométriques, même résultat, si tu pense qu'on a la suite des puissances d'un demi privée de sous-suites géométriques c'est pareil, au final au mieux tu auras une suite chaotique sans raison.
Et dans ce cas ta recherche n'a aucun intérêt, des formules pour Pi il en existe comme:

Tu pars de 4 tu retire 4/3, tu remet 4/5, tu retire 4/7 et ainsi de suite, tu tourne autour de pi en t'approchant toujours plus. Connu en Inde au Vème siècle.
Quant à cette formule proposée j'ai l'impression que celui qui l'a écrit tente de paver la différence entre le carré et le quart de disque par des petits carrés qui sont d'aires proportionnelles au carré EFGH avec des facteurs 1/2^n sauf que ça ne peut fonctionner vu qu'ils ne collent pas au cercle:
Pièce jointe 189835

Merci pour ta réponse.
Oui la démarche consiste bien à "paver" avec des carrés la surface ( 4R² - Pi*R² ).
On part d'une "réciproque du cercle" : Pour 2 carrés donnés a et b tel que b est le double de a
alors il existe un unique carré c qui possède tel que l'aire de c est de même aire que le cercle qui circonscrit le carré a et inscrit dans le carré b.
Ensuite on construit un carré qui est l'aire de la différence entre carré b et carré c c'est à dire la surface ( 4R² - Pi*R² ) et on cherche à faire une quadrature de ce carré à partir de carrés dans une proportion du petit carré e, carré qui a pour côté R* sqrt ([ ( 3/2 ) - sqrt (2) ] ).

[Guimzo]

Bonjour,




Voici une petite approximation de Pi ...
Soit un carré de côté a alors le Rayon R du cercle ayant la même aire que le carré a est proche de :


R = a*sqrt(2) - { a* [ (sqrt(2) + 1 ) / 2*sqrt(2) ] - ( 3/850 ) }

Par extension une approximation de Pi :

1 / [ (1 981 793 /1 445 000 ) - ( 633*sqrt(2) / 850 ) ]