DM Term S Nombre complexes

[Alix5]

Bonjour !



Alors voilà, je suis bloquée à la question 5.de mon DM sur les nombres complexes. Donc voilà les questions qui sont (je pense) utiles pour y répondre :

Le plan (P) est rapporté à un repère orthonormé direct (0,vecteur u, vecteur v), unité graphique 3cm. On considère l'application f de C (ensemble des nombres complexes) définie par f(z)=(z+1-2i)/(2+z+i).

3. En posant z=x+iy, x et y étant des réels, déterminer la partie réelle et la partie imaginaire de f(z).

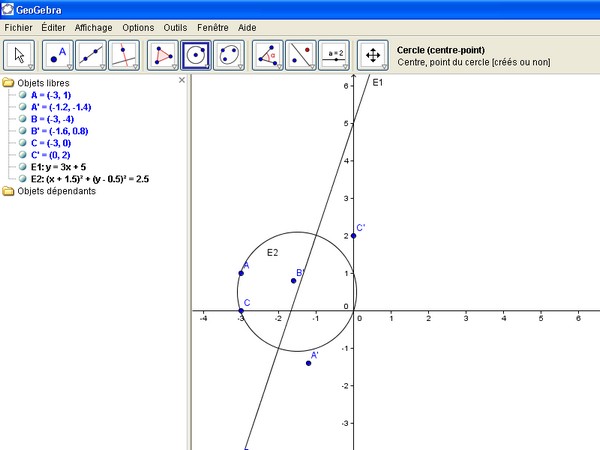
5. Déterminer et représenter dans (P) l'ensemble E2 des points M dont l'affixe z est telle que f(z) est imaginaire pur.


Donc voici ce que j'ai trouvé pour les questions :

3. Ici j'ai trouvé que Re(f(z))=(x²+y²+3x-y)/((x+2)²+(y+1)²) et que Im(f(z))=(-3x+y-5)/((x+2)²+(y+1)²)
Je trouve ça quand même lourd comme résultat au final et je vois pas si je peux réduire plus ou pas. Est-ce qu'il faut réduire plus ou pas ?

5. Donc j'ai dit que f(z) imaginaire pur équivaut à dire que Re(f(z))=0 donc après j'ai développé et j'ai trouvé que y²-y=-x²-3x.
Donc à partir de là je bloque je sais pas comment développer pour arriver à un ensemble comme une équation de droite ou plusieurs équations de droites. Est-ce que vous pourriez m'aider à débloquer tout ça pour que je puisse continuer ?


Merci d'avance pour vos réponses.
-----

[gg0]

Bonsoir.

Je ne vérifie pas tes calculs, je te fais confiance. Re(f(z)) et Im(f(z)) ne se "réduisent" pas.
Pour le 5, tu as fait une transformation sans intérêt alors que x²+y²+3x-y=0 est une équation de type bien connu

Cordialement.

Nb : ça fait plaisir, quelqu'un qui ne demande pas de tout faire !

[numpo]

Bonsoir,
- J'ai vérifié et je retombe sur les mêmes résultats que toi pour Re et Im.
- Si tu ne vois toujours pas pour la 5, pense à mettre x²+3x sous forme canonique, et de même pour y²-y
Tu tomberas alors sur une équation de la forme : (x-a)²+(y-b)²=R²
Voilà

[Alix5]

Merci beaucoup pour vos réponses !

En gros si je me souviens bien, ces deux équations en fait c'est les mêmes et puis c'est des équations de cercle, c'est ça ?

[A voir en vidéo sur Futura]

[Alix5]

Voici ce que je trouve au final :

L'ensemble E2 correspond au cercle d'équation (x+(3/2))²+(y-(1/2))²=(racine(10)/2)², de rayon r=racine(10)/2 et de centre O(-3/2;1/2).

Vous croyez que c'est bon ?

Merci pour votre aide en tout cas !

[numpo]

Oui c'est bon

[Alix5]

D'accord

Bon je suis désolée mais j'ai un second problème toujours dans le même exo. À la dernière question on me demande de vérifier avec les points de la question 1 et 2.
Ces points ce sont A(-3+i), A'(-6/5-7/5i), B(-3-4i), B'(-8/5+4/5i), C(-3) et C'(2i).
À la question 4. c'était pareil que pour la 5. mais pour un affixe réel, donc j'ai trouvé y=3x+5.
Alors selon moi, C c'est un affixe réel et C' un imaginaire pur. Sauf que quand je fais un calcul pour vérifier ou quand je vérifie sur ma calculatrice, le résultat ne correspond pas. Et en plus B appartiendrait à E1 alors que pour moi non.

Est-ce que je me trompe dans mon raisonnement ? Parce que vous me dites que c'est bon, j'ai vérifié mes calculs ils me semblent bon, je ne comprends pas. Vous avez une idée ?

[gg0]

Je ne sais pas quel calcul tu fais ...
Pour C, z=-3 et f(z) est bien un imaginaire pur. C(-3,0) est bien sur le cercle.

Cordialement.

[Alix5]

Mais il me semble qu'il faut que ce soit l'imaginaire pur donc C' qui soit sur le cercle puisque ce cercle c'est l'ensemble des points M dont l'affixe z est telle que f(z) est un imaginaire pur, nan ?

[Alix5]

En fait quand je fais la figure sur GeoGebra, je me rends compte que j'ai dû me tromper dans mes calculs de la première question. puis que je crois que A' est censé être imaginaire pur parce que A se trouve sur le cercle et que B' est censé être un réel parce que B se trouve sur la droite, c'est ça non ?

[Alix5]

C'est ce que j'ai fait sur GeoGebra

[Alix5]

C'est bon j'ai trouvé mon erreur et en corrigeant, ça marche ! En fin de compte je m'étais trompé dans la toute première questions où on me demandait de calculer f(z) pour les points A et B, j'avais multiplié leur affixe par deux dans le numérateur au lieu de laisser 2i. Et puis j'avais compris à l'envers les questions 4. et 5., je pensais que c'était z qui devait être un réel ou un imaginaire pur, alors que c'est f(z).

En tout cas, merci beaucoup pour votre aide !

[zultrane]

bonjours, comment avez-vous trouvez Re(z) et Im(z) ?

[gg0]

Heu ... c'est du cours. Une fois z mis sous la forme algébrique z=a+ib (a et b sont des réels), Re(z)=a et Im(z)=b. C'est tout !

Cordialement.