Repère orthonormé et trigonométrie.

[NexXxuS]

Bonsoirs, j'aurai besoin d'une petite aide pour 2 bouts d'exercices où j'ai absolument rien compris. Pour l'exercice de trigonométrie, j'ai rien compris car j'étais absent à certains cours à cause de fête religieuse (J'ai tous le cours, mais je suis du genre à apprendre avec des exercices en cours.) et pour le repère orthonormé je n'ai tous simplement pas compris ! :/

Commençons :
-Soit (O,I,J) un repère orthonormé du plan.
On considère les points A(1;2) ; B(5;2) ; C(3;2+3√2)
Quelle est la nature exacte du triangle ABC?

Je sais pas comment trouver l'ordonnée du point C.. :/

P.S: Pour cette exercice je n'ai absolument rien a gagné, ce n'est pas un DM ou autre. C'est juste un exercice que j'avais envie de faire pour ma culture.

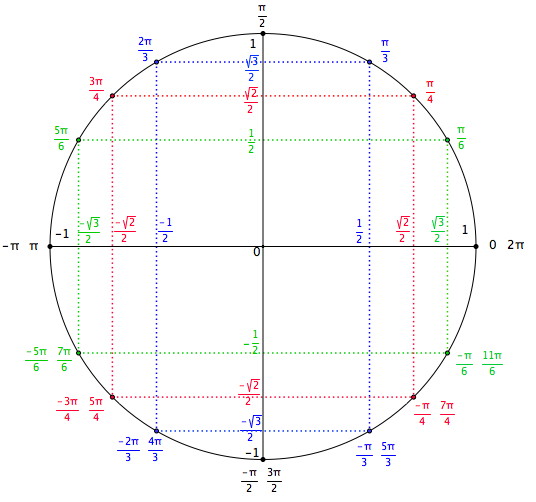
-1. Déterminier un nombre réel a' de l'intervalle ]-π;π] permettant de placer le point associé au réel -29π/6 puis le placer sur un cercle trigonométrique.

2. On sait que sin(x)=-0,2 et que x ϵ [π/2 ; 3π/2]
a. Placer le point sur un cercle trigonométrique.
b. Calculer la valeur exacte de cos(x) puis en donner une valeur approchée au dixième près.

P.S: Pour cette exercice, c'est un DM, j'aurai besoin de beaucoup d'aide car je n'ai pas compris le fin de chapitre de la trigonométrie. En précisant que je n'ai absolument rien compris..

Merci d'avance pour votre aide.
-----

[NexXxuS]

Personne pour m'aider ou me donner un petit conseil? :/

[NexXxuS]

Toujours personne ? :/
Pour le premier exercice j'ai fait
AB=√(5-1)²+(2-2)²
AB=√16+0
AB=4

AC=√(3-1)²+(2-2+3√2)²
AC=√(4+3√2²)
AC=2+√6

BC=√(5-3)²+(2-2+3√2)²
BC=2+√6

Le triangle ABC est isocèle en C. Est ce que j'ai bon ?
Et pour la trigonométrie j'ai toujours pas compris.. :/

[gg0]

Bonsoir

"Je sais pas comment trouver l'ordonnée du point C" ??? elle est donnée !
Ensuite, quand tu as fait la démonstration, tu fais une erreur de signe :
AC=√(3-1)²+(2-2-3√2)²
car soustraire une somme, c'est soustraire chacun des termes. Idem pour BC. Heureusement pour toi cette erreur de calcul disparait dans l'élévation au carré.

Pour la trigo :

1) si tu ajoutes 2pi ou soustrais 2pi, tu reste au même point du cercle trigo. A toi de jouer.
2) Tu places -0,2 sur l'axe des sinus, tu regarde les points du cercle qui se projette,t là, tu choisis le bon. Pour calculer cos(x), tu as une relation qui relie sin et cos. Il y a juste à choisir le bon signe, mais tu le connais en regardant le point sur le cercle.
Si tu ne me comprends pas, lis et relis un cours de trigo. Moi, j'ai supposé que tu connaissais les bases.

Cordialement.

[A voir en vidéo sur Futura]

[NexXxuS]

Merci à toi gg0 pour ta réponse.

-Pour la correction, merci. Mais es-tu sûr ? Car C(3;2+3√2) à la base. AC=√(xa-xb)²+(ya-yb)² et yb=2+3√2 .. :/

1. J'ai pas trop compris la question en entier et surtout "Déterminier un nombre réel a' de l'intervalle ]-π;π]" pour commencer :
Il faut faire -29π/6 = π/6 - 30π/6
= π/6 - 5π
C'est bien ça ? Et après essayer de le placer sur un repère, pas trouvé. :/

2. D'accord j'ai compris ! Mais x ϵ [π/2 ; 3π/2] sert à quoi dans l'énoncer ?
Et la relation qui relie cos(x) et sin(x) c'est bien (cos(x))²+(sin(x))²=1
Donc :
(cos(x))²+0,2²=1
cos(x)=1-0,2
cos(x)=0,8
Si j'ai bien compris, ça c'est la réponse au petit b. ?

[NexXxuS]

Petit up..

[gg0]

2-(2+3√2) =2-2-3√2
depuis la cinquième ! Il n'y a pas de changement des règles de base du calcul.

= π/6 - 5π aucun intérêt, c'est 2Pi qu'on peut ajouter ou soustraire

(cos(x))²+0,2²=1
cos(x)=1-0,2 ???
les carrés, c'est seulement pour faire beau ?

Donc globalement, tant que tu n'appliques pas les règles de calcul, tu fais faux. Arrête de faire faux, c'est facile : Tu ne modifies qu'avec une règle de calcul.

[NexXxuS]

D'accord merci pour la correction.

Le point -29π/6 se trouve à -π/6 dans le cercle trigonométrique car c'est 29 fois le tour du cercle, et il faut l'expliquer comment on trouve ça non ?
"= π/6 - 5π aucun intérêt, c'est 2Pi qu'on peut ajouter ou soustraire" J'ai pas compris ce point, pourquoi il n'y aucun intérêt ? On demande l'intervalle entre ]-π;π] donc il faut décortiquer cela non ?

(cos(x))²+0,04=1
cos(x)=√0,96 ~0,98.
Ça correspond à la réponse de la question 2.b. ?

Je voudrais juste savoir à quoi sert les explications "x ϵ [π/2 ; 3π/2]" et "Déterminier un nombre réel a' de l'intervalle ]-π;π]", ils n'influencent pas les questions?
Et merci pour tes réponses gg0.
Cordialement.

[gg0]

Le point -29π/6 se trouve à -π/6 dans le cercle trigonométrique car c'est 29 fois le tour du cercle,

J'espère que tu es moins endormi qu'hier soir et que tu réalises l'absurdité !
Sans compter qu’un tour du cercle fait .... 2π.

Le mieux est que tu places sur ton cercle 0, -π/6, 2(-π/6), 3(-π/6), 4(-π/6), 5(-π/6), ...29(-π/6)=-29π/6.
Tu comprendras probablement mieux ce qui se passe. fais-le !

cos(x)=√0,96 et pourquoi pas -√0,96 ??

"Je voudrais juste savoir à quoi sert les explications "x ϵ [π/2 ; 3π/2]" et "Déterminier un nombre réel a' de l'intervalle ]-π;π]", ils n'influencent pas les questions?" Si, bien sûr. Mais tant que tu n'es pas strict dans tes démonstrations (par exemple a²=b² ne donne pas a=b, mais ... et tu avais à le savoir depuis des années) tu ne peux pas en avoir besoin, tu agis sans savoir.

Cordialement.

[NexXxuS]

Bonjours à toi gg0.
Je me suis compris en disant "Le point -29π/6 se trouve à -π/6 dans le cercle trigonométrique car c'est 29 fois le tour du cercle", j'ai cherché sur internet et ça a confirmé ce que je pensais et je vais te montrer ce que je voulais réellement dire.

Il se trouve en bas à droite.
Là j'ai réussi à le placer, mais comment on arrive à déterminer ce point ? C'est en sachant que -π/6=-29π/6 ? Tu penses que c'est une bonne démonstration ?

J'ai pas compris "cos(x)=√0,96 et pourquoi pas -√0,96"
Refaisons le calcul :
Sachant que sin(x)=-0,2 et que (cos(x))²+(sin(x))²=1
(cos(x))²-0,2²=1
(cos(x))²+0,04=1
(cos(x))²=1-0,04
cos(x)=√0,96 (Pourquoi -√0,96 ? Je comprends pas, c'est clairement positif !)
cos(x)~0,98 et on demande au dixième près donc c'est 1.

Et encore merci de tes réponses.

[NexXxuS]

J'ai rien dit tu as raison, ça fait bien -√0,96~-0.97, au dixième près c'est -1, rien que sur le figure trigonométrique, ça se voit, que suis-je bète.

[NexXxuS]

Petit UP.

[gg0]

Bonsoir.

Il se trouve en bas à droite.

pas vu

Là j'ai réussi à le placer, mais comment on arrive à déterminer ce point ? C'est en sachant que -π/6=-29π/6 ? Tu penses que c'est une bonne démonstration ?

Ce n'est pas une bonne démonstration car -π/6=-29π/6 est archi faux !! -π/6vaut environ -0,5 et -29π/6 29 fois plus !!de l'ordre de -15
Tu n'as toujours pas compris ce que je te disais : Si tu ajoutes 2π, tu arrives au même point (pas à la même valeur) regarde sur ta figure pour -3π/4 : -3π/4+ 2π= ??
Alors tu regardes ce que ça donne en ajoutant 2π autant de fois que nécessaire. Sans tricher : en faisant les calculs correctement.

cos(x)=√0,96 (Pourquoi -√0,96 ? Je comprends pas, c'est clairement positif !)

Je ne comprends pas ! que √0,96 soit clairement positif,c'est évident, c'est la définition d'une racine carrée. mais pourquoi as-tu dit que cos(x) est une racine carrée ?
J'explique ce que tu devrais savoir depuis longtemps : (-2)² = 4, mais -2 n'est pas la racine carrée de 4 : la racine carrée de 4 est 2.
Tu obtiens (cos x)² = 0,96 ce qui te donne deux possibilités soit -√0,96 soit √0,96. laquelle est la bonne ?

Cordialement.