DM de math Trigonométrie

[Matheux56]

Bonjour

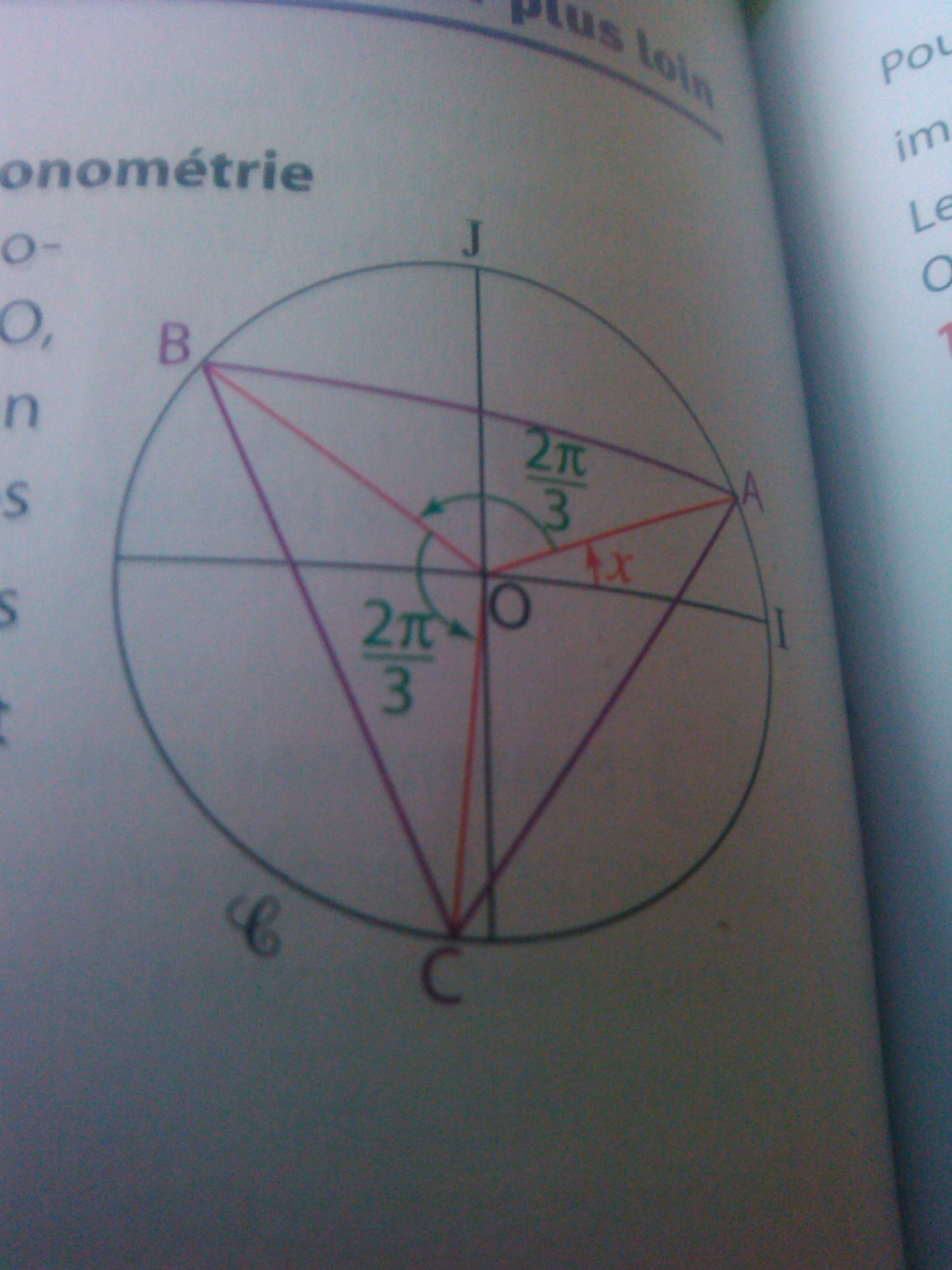
énoncé : Sur le cercle trigonométrique C de centre O, A est le point image d'un nombre réelx, B et C les points images respectifs des nombres réels x + 2pi/3 et x + 4pi/3.

1. Démontrer que le triangle ABC est équilatéral.
2.a) Démontrer que : Vecteur (OA)+ Vecteur (OB)+ Vecteur (OC) = Vecteur nul
b) En déduire que : cos x+cos (x+2pi/3)+ cos(x+4pi/3) = 0
et sin x + sin(x+2pi/3) + sin(x+4pi/3) = 0

3) Prouver alors les égalités : cos pi/9 + cos 7pi/9 + cos 13pi/9 = 0
et sin pi/9 + sin 7pi/9 + sin 13pi/9 = 0



1. Je suppose qu'il faut jouer avec les angles mais je ne vois pas trop comment .. car dans les 2pi/3 il y a aussi x compris a ce que je vois

2.a) Par décomposition peut etre mais je ne vois pas vraiment le truc ...

Pour le reste des questions j'ai besoin des deux 1ère pour avancer..

Merci d'avance
-----

[gg0]

Bonjour.

1) Comment démontre-t-on qu'un triangle est équilatéral ? Il y a de nombreuses méthodes, cherche-en une qui correspond à la situation (il y en a plusieurs possibles).
2) Qu'est O pour le triangle ? que sais-tu de ce point quand le triangle est équilatéral ?

Bonne réflexion !!

[Matheux56]

1) les seuls méthodes que je connaisse sont soit de montrer qu'il a deux coté égaux ou bien 2 angles égaux ?
2) O représente le centre de gravité ?

[Matheux56]

1) Ha jme suis trompé j'voulais dire démontrer qu'il a 3 cotés égaux ou 3 angles égaux !

[A voir en vidéo sur Futura]

[gg0]

Combien mesurent les angles des triangles OAB, OBC et OCA ?

D'autre idées sur le triangle équilatéral :
ABC est équilatéral si et seulement si :
* deux de ses angles font pi/3 radians
* le centre du cercle circonscrit est confondu avec l'orthocentre, ou le centre de gravité, ou le centre du cercle inscrit.
* deux côtés sont égaux et l'angle entre ces deux côtés fait pi/3

Il y en a sans doute d'autres, mais tu as déjà suffisamment de "billes" pour finir....

Cordialement.

NB : Pour bien raisonner en maths, il faut connaître les propriétés utiles, donc avoir bien appris au fur et à mesure. Si on n'a pas appris avant, il faut s'y mettre, réapprendre ....

[Matheux56]

Je n'ai pas appris encore avec pi/3, désolé ^^
Donc je vais utilisé la 1ère solution. Donc OAB = x , OBC = x , et OCA = x
On sais qu'un angle de 80° est égal a pi/3 et que 180° est égal a pi
Si on arrive a prouver que B = pi/3 A = pi/3 et C = pi/3 alors nous pourront dire que le triangle est équilatéral.
Chaque angle est égal à 2pi/3 - x non ?

[Matheux56]

*pi/3 = 60 ° pardon

[Samuel9-14]

Non.
Que sais tu des triangles OAB, OBC et OCA ?
Sahcnat que OA=OB=OC (A, B et C sont sur un même cercle de centre O)

[gg0]

Travaille en degrés si tu préfères,

mais trouver combien valent les angles OAB et OBA est un exercice de cinquième, une fois traduit en degrés la valeur de l'angle AOB.

[Matheux56]

Bah ce sont des angles inscrits et des angles inscrit interceptant le même cercle on la même mesure ?

[Samuel9-14]

Bien plus simple que tout ça, OA=OB, donc OAB est isocèle. Que sais-tu d'un triangle isocèle ?

[Matheux56]

Isocèle : deux angles égaux ainsi que 2 cotés égaux.

[Samuel9-14]

Okay !
Et la somme des angles dans un triangle ?

[Matheux56]

La somme des angles est de 180° xD

[Samuel9-14]

Tu rigoles mais si tu avais vu ça avant, ta question serait terminée depuis longtemps

Donc t'en déduis quoi pour les angles OBA et OAB ?

Tu fais pareil dans chaque triangle (OBC et OAC) et tu trouves les mesures d'angles du triangle ABC. Tu en déduis qu'il est équilatéral.

[Matheux56]

Ha mais oui xD. Mais si on fonctionne avec ca tout les angles sont égals a x (angles internes-internes) ?

[Samuel9-14]

Quels angles ? Ceux du triangle ABC ne valent pas x !

[Matheux56]

Ha mais GRRRR ►.◄. Ils valent 1/2 de 2pi/3 ?

[Samuel9-14]

Oui c'est ça... Je me demande comme tu arrives à ce résultat en passant par 1/2 mais oui, oui c'est ça ^^

[Matheux56]

bah les angles inscrits sont égales a 1/2 de l'angle au centre ?

Mais si vous avez un méthode plus math ou mieux, j'aimerai bien la savoir x) !

[Samuel9-14]

Ben j'ai calculé tous les angles en m'aidant du fait que les triangles sont isocèles. Et pour trouver les angles de ABC, il ne reste qu'à additionner BCO et OCA etc...

[Matheux56]

Pour 2.a) Démontrer que : Vecteur (OA)+ Vecteur (OB)+ Vecteur (OC) = Vecteur nul

je vois pas trop comment m'y prendre x)

[Matheux56]

Si je met mais ABC est inscrit dans le cercle de centre O. O est donc le point de concours des médiatrices du triangle c’est aussi son centre de gravité ==> OA+OB+OC=0"

[Samuel9-14]

Tu ne sais pas additionner des vecteurs ? C'est pareil pour 2,3, 4, 5, 6 vecteurs...

Sinon, je ne sais pas si la propirété existe mais dans triangle équilatéral, la somme des vecteurs de chaque côté du triangle est égale au vecteur nul. Mais je ne sais pas si on peut l'utiliser

[gg0]

Tu peux aussi construire la somme de deux des vecteurs et prouver que c'est l'opposé du troisième.
Une idée plus jolie : Si on fait une rotation de centre 0 d'angle 2Pi/3, la somme est inchangée, donc c'est le vecteur nul, le seul à se conserver par cette rotation.

Cordialement.

[Matheux56]

En déduire que : cos x+cos (x+2pi/3)+ cos(x+4pi/3) = 0
et sin x + sin(x+2pi/3) + sin(x+4pi/3) = 0

Si on fait une rotation de centre 0 d'angle 2Pi/3, la somme est inchangée, donc c'est le vecteur nul, le seul à se conserver par cette rotation.

Cordialement.

Ca réponds a cette question aussi Oo ?

[Samuel9-14]

A quoi correspond cos x+cos (x+2pi/3)+ cos(x+4pi/3) et sin x + sin(x+2pi/3) + sin(x+4pi/3) ?
Il est alors facile d'en déduire que ces somems sont nulles.

[Matheux56]

Il correspond au angle A,B et C ?

[gg0]

Tu viens juste d'additionner trois vecteurs, n'auraient-ils pas un rapport ????

[Matheux56]

C'est c'que je voulais dire en faite x), désolé j'me suis mal exprimé et merci :3