Bonjour!
Je cherche à résoudre algébriquement l'inéquation sin(x)<1/2 dans l'intervalle I=]-pi; pi]
J'ai essayé de résoudre dans R et ensuite j'ai cherché les solutions dans I:
Je n'arrive pas à faire apparaître la solution complète...
Je dois me tromper quelque part, mais je ne vois pas où..
Merci pour votre aide
Bonjour,
Tu m'étonnesEnvoyé par Jon83
Relis attentivement toutes les inégalités que tu viens d'écrire, ... il n'y a rien qui te choque ?!!
Cliquez pour afficher
Dernière modification par PlaneteF ; 01/02/2013 à 14h51.
Oui, en effet, j'ai écrit de grosses c....sBonjour,
Tu m'étonnes
Relis attentivement toutes les inégalités que tu viens d'écrire, ... il n'y a rien qui te choque ?!!
Cliquez pour afficher
En fait, mon cours dit qu'il faut d'abord résoudre l'équation trigonométrique correspondante:
ici sin(x)=1/2 donne x=pi/6+2k.pi ou x=pi-pi/6 + 2k.pi dans R
Ensuite, j'ai du mal à passer aux inégalités....
Bonsoir.
Deux méthodes simples pour passer aux inégalités :
* Si on connaît bien la fonction sinus et ses variations, on applique. par exemple, le sinus est croissant sur [-pi/2;pi/2], donc supérieur à 1/2 de Pi/6 à pi/2; puis il décroît sur [pi/2, pi], donc ...
* On peut aussi utiliser le cercle trigonométrique comme "outil à comprendre", représenter les pi/6+2k.pi et pi-pi/6 + 2k.pi, représenter -pi et pi, regarder et conclure.
Cordialement.
Merci à tous pour vos réponses!
J'ai trouvé ce document très bien fait:
http://mathzone.blog.free.fr/public/...ometriques.pdf
ça rafraîchit bien la mémoire et ça m'évitera à l'avenir d'écrire de énormités...
Bonjour.
Si tu avais bien écrit ta 1ere ligne:
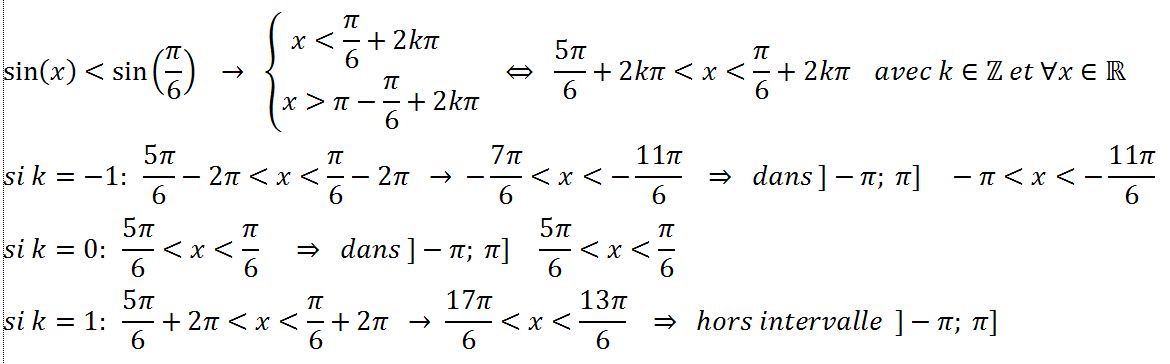
tu aurais pu continuer ce que tu as fait (attribuer des valeurs à k bien choisies).
