DM Maths Géométrie et Produit scalaire Term S

[Alix5]

Bonjour à tous,

J'ai quelques petites difficultés à résoudre 2 questions de mon DM pour jeudi. Ces questions sont la 2.b) et la 3.b)

Voici l'énoncé des questions :

2. Avec le produit sclaire
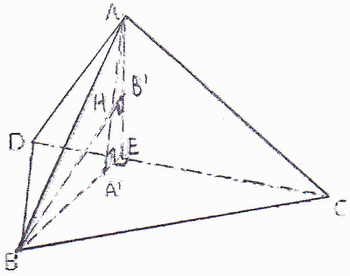
ABCD est un tétraèdre.
a) Démontrer que si .=0 et .=0, alors .=0. -> J'ai réussi à faire celle-ci. Mais la suivante non.
b) Démontrer que si le tétraèdre ABCD est orthocentrique, alors .=.=.=0. -> Ici je bloque je ne vois pas comment résoudre ceci. Pourriez vous m'aider à débloquer tout ça ?

3. Avec la géométrie
Réciproquement, ABCD est un tétraèdre dont les arêtes opposées sont deux à deux orthogonales.
Dans le triangle BCD, E est le pied de la hauteur issue de B.
Dans le triangle ABE, A' et B' sont les pieds des hauteurs issues de A et B et H est l'orthocentre.

a) Démontrer que la droite (AA') et le plan (BCD) sont orthogonaux.
b) Démontrer que la droite (CH) et le plan (ABD) sont orthogonaux. -> Ici aussi je bloque. Je pensais dire que c'était le cas parce que H est l'orthocentre et donc la hauteur issue de C passe par H. Sauf que H est l'orthocentre de ABE et pas du tétraèdre. Qu'en pensez-vous ? Y a-t-il un autre moyen de démontrer ceci ?

Merci d'avance pour vos réponses
-----

[sammy93]

Bonjour.
Vous avez démontré que si .
Vous devez aussi démontrer que si et enfin que si .
Sauf erreur de ma part.

[sammy93]

J'ai très mal lu le sujet et je retire toutes les betises écrites.
Je vous présente toutes mes excuses.

[sammy93]

Re.
ABCD orthocentrique donc (AA') et (BB') se coupant en H sont dans un meme plan.La droite (DC) est orthogonale à (AA') [car (AA') orthogonale au plan
(BCD) ] et à (BB') [car (BB') orthogonale au plan (ACD)]. Vous pouvez en déduire que (CD) est orthogonale au plan (AA'BB') donc à (AB) d'ou:
.
Voilà,vous avez la 1ere condition du a) ,à vous de trouver la 2eme pour terminer.....
J'espère cette fois-ci que c'est sans erreur.

[A voir en vidéo sur Futura]

[inviteb99bdf36]

J'ai le même Dm de maths à faire, comment tu as fais pour démontrer que la droite (AA') et le plan (BCD) sont orthogonaux?
Je n'arrive pas à trouver...

[thierthier]

Salut Didine. en gros tu doit prouver que (AA') est othogonal à deux vecteurs non colinéaires de (BCD), maintenant essaie de voir quels vecteurs tu peux prendre

[inviteb99bdf36]

Oui, d'accord mais comment? Déjà, je sais que AA' est la hauteur issue de A, (AA') perpendiculaire à (BE). Mais autrement, on dit que la hauteur d'un tétraèdre est la droite passant par un sommet et orthogonale au plan de la face opposée. Donc là, la face opposée, ce serait (BCD)? Et du coup, ça suffirerait à dire que la droite et le plan sont orthogonaux?