Problème dérivation d'une fonction

[inviteb2d1a1bb]

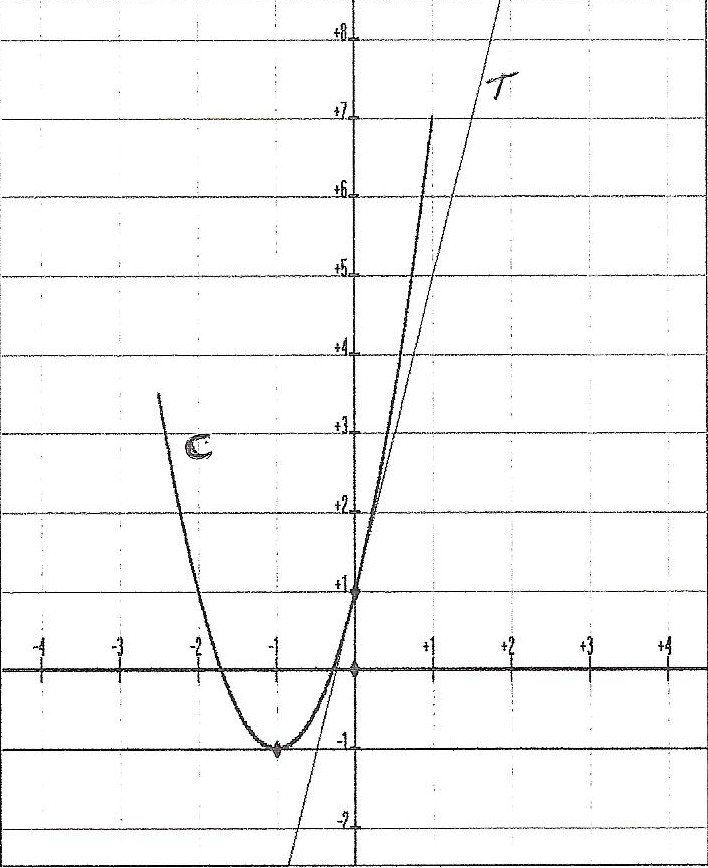
Bonjour, j'ai un exercice à réaliser sur la dérivation mais une question attire mon attention car je ne comprend pas l'énoncé de celle-ci. Voici la question : Utiliser les deux questions précédentes pour montrer que a=2 et b=4. Les deux questions étaient de trouver une dérivation, la voici f'(x)=2xa+b sachant que l'expression de départ était f(x)=ax²+bx+c et de déterminer graphiquement f'(-1) et f'(0), les déterminations graphiques sont f'(-1)=0 et f'(0)=4. Pour répondre à la question, je pensais qu'il fallait refaire le calcul de la dérivation en remplaçant a par 2 et b par 4 mais je pense que ce n'est pas ça.
-----

[Lil00]

Bonjour,

Tu sais que f'(-1)=0 et f'(0)=4.

Tu sais aussi que f'(x)=2ax+b.
Tu remplaces x dans cette équation, une fois par -1 et une fois par 0, et tu obtiens deux équations avec a et b, qu'il n'y a plus qu'à résoudre.

[invite4842e1dc]

Bonjour

ATTENTION ce que tu as écrit est faux car tu confonds plusieurs "objets"...

Si f(x)=ax²+bx+c

tu as raison d'écrire que f'(x)=2ax+b


Par contre si tu "observes" sur ton graphique que
f'(-1)=0 et que f'(0)=4 alors VOILA "exactement" ce que cela veut dire :

f'(-1)=0 <==> 2a(-1)+b =0 <==> -2a+b=0

et

f'(0)=4 <==> 2a(0)+b =4 <==> b=4


PUIS en résolvant ce système de 2 équations à 2 inconnues on trouve que a=2 et b= 4


Question : Es tu d'accord avec ces explications ?

[inviteb2d1a1bb]

D'accord merci pour votre aide, je comprend maintenant l'étape des deux équations à deux inconnues. Je suis d'accord avec vos explications.

[A voir en vidéo sur Futura]

[inviteb2d1a1bb]

Bonjour, suite à votre réponse j'ai réussi à résoudre la double équation à deux inconnues. Mais je suis confronté à un autre problème malheureusement. En remarquant que (C) passe par le point, je dois déterminer la valeur de c et en déduire l'expression de f(x). Mais je ne sais sur quelle piste me lancer. Voici pour aider la courbe.

[jamo]

tu vois bien que f(-1)=-1 alors tu peux déduire c car tu connais a et b .

[inviteb2d1a1bb]

D'accord merci mais j'ai vu que f(-1)=1 mais je ne vois pas comment déduire c en fonction de a et b ? Cordialement.

[Samuel9-14]

Pour déterminer c, il faut que ax²+bx s'annule, comme ça il ne te reste plus que c et tu aruas f(x)=c donc tu pourras déterminer c graphiquement. Pour quelle valeur de ax²+bx s'annule-t-il ?

[inviteb2d1a1bb]

D'accord, je comprend votre démarche, mais les valeurs pour lesquelles ax²+bx s'annule sont a=2 et b=4 ? Cordialement?

[jamo]

je ne sais pas si tu comprends ce que tu écris , a et b ont été déterminés ( cf message 3) et tu dis que "mais les valeurs pour lesquelles ax²+bx s'annule sont a=2 et b=4 ?"
f(x)=ax²+bx+c comme tu connais a et b donc f(x)=2x²+4x+c
il faut déterminer c , comme f(-1)=-1 donc tu reviens avec la valeur de c .tu en as pour 30s

[Samuel9-14]

Non, a et b sont des constantes, leur valeur ne change pas.
Ton trinôme s'écrit :
2x²+4x+c.
Pour quelle valeur de x 2x²+4x s'annule-t-il ?
Comme ça tu as f(x)=c (pour la fameuse valeur de x). Et tu en déduis c graphiquement.

[inviteb2d1a1bb]

Ok, 2x²+4x s'annule lorsque la valeur de x est -2 car 2 X (-2)² + 4 X (-2) = 0.

[Samuel9-14]

Ok, donc du coup t'en déduis quelle valeur de c ?

[inviteb2d1a1bb]

J'en déduis donc que f(x)=c. Mais je ne vois qu'elle peut-être la valeur de c ! La valeur de c est-elle 0 ? Cordialement.

[Samuel9-14]

Non, tu en déduis pas que f(x)=c, tu en déduis que f(-2)=c.
Et là tu peux lire graphiquement c (l'image de -2 par la fonction f).

[inviteb2d1a1bb]

Et donc l'expression de f(x) est f(-2)=c ? Cordialement.

[Samuel9-14]

Non !
f(x) a une seule expression qui est 2x²+4x+c.
x est une variable, c est une constante.
f est fonction de x. Ici on remplace x par 0 (-2 ou 0 c'est pareil).
f(0)=2*0²+4*0+c
f(0)=c.

L'image de 0 par la fonction f est c.
Or si tu lis graphiquement l'image de 0, tu trouves quoi ? Tu trouves la valeur de c.