Bonjour à tous!
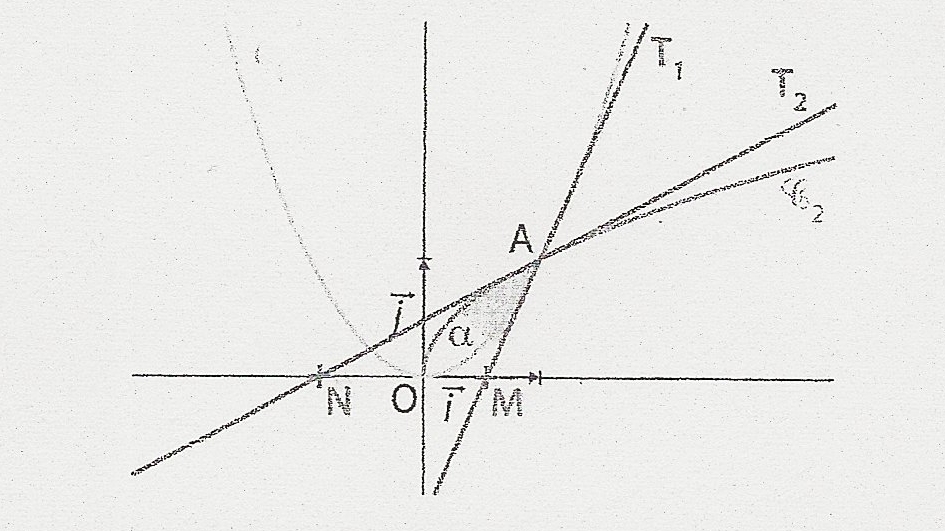
"Dans un repère orthonormal (o, i, j), les courbes C1 et C2 ont pour équation respectives y=x² et y= racine de x. Les tangentes T1 et T2 en leur point commun A coupent l'axe des abscisses respectivement en M et N.
1)a) Trouvez une équation de T1 et T2
b) Déduisez en les coordonnées de M et N
2) Trouves, arrondie à un degré près, une mesure alpha de l'angle MAN"
1)a) y = f '(a) (x - a) + f(a) Comment faire après?..
Ben ...
Trouver l'abscisse (a) du point commun, puis appliquer la formule aux deux courbes de fonctions :
y=f(x)=x²
y=f(x)=rac(x)
Bon travail !
NB : une formule n'a d'utilité que si on sait ce que signifient ses notations (symboles, lettres, ...).
PS : Pourquoi ce titre, il n'y a pas de cercle ???
Comment je trouve l'abscisse du point A?
Merci de votre aide!
Tu résous simplement l'équation x²=rac(x) ! Et là tu vas trouver l'abscisse du point d'intersection des deux courbes, qui est A.
Petit problème : Il y a deux points !
Il y a peut-être une figure qui permet de choisir.
x=racine carré de la racine carré de x? o_o
Je suis perdue..
Voila la figure!
Sur la figure, les courbes se coupent en 2 points, l'origine, et A. A est donc l'autre.
Pour l'équation
la méthode habituelle est de tout passer dans un même membre et de factoriser. ici, les deux membres étant positifs, on obtient une équation équivalente en élevant au carré.
Sinon, on peut facilement deviner la valeur de a, et montrer (inégalités simples) qu'il n'y a que ce a et 0 qui conviennent.
Mais en tout cas, c'est ton exercice, c'est toi qui calcules...
Non, puisqu'il n'y a pas de tangente en 0 pour la fonctionEnvoyé par gg0
..
Si, si, il y a bien une tangente, mais pas de dérivée.
y=f'(a)(racinex -2) +1 ?
(Quelle est son équation ?)
Bonsoir,
Dernière modification par PlaneteF ; 21/04/2013 à 22h47.
Mes excuses alors, je pensais que si ce n'était pas dérivable, il ne pouvait pas y avoir de tangente..
La démonstration est-elle à la portée d'un Terminale ? (Désolé de m'approprier la discussion une fois de plus..)Bonsoir,
D'ailleurs, pour être plus précis, puisqu'il s'agit d'une demi-tangente :
Dernière modification par PlaneteF ; 21/04/2013 à 23h32.
Et la démonstration dans tout ça ? ^^'
Donc pour la première y = 0 (0-2)+1 = 1 ?
Pour la tangente à la courbe représentative de
Applique bien ta formule
y= 0 ( racinex -2) +1 ?
Je rappelle qu'on a
j'avais lu a à la place d'alpha..
y= f'(alpha)(0-1)+1
Comment trouver la dérivé d'alpha?..
Mais
Là, le point en question c'est
Donc l'équation de la tangente à la courbe représentative de
Il suffit juste d'appliquer la formule maintenant..
Ah d'accord je n'avais pas compris ça! merci!
Hum, comment ça appliquer?..
Il serait peut-être temps de comprendre..
Eh bien, ta fonction ici, c'est
(On va pas faire les choses à ta place non plus..)
y=f'(1)(racinex - 1)+f(1) ?
Bon, je veux bien être patient, mais là je trouve que t'abuses un peu..
Ta fonction
C'est pourtant pas compliqué.. Que vaut
y = 1/2racine de 1 * (x-1) + racine de 1 = 1/2 (x-1) +1 ?
Désolé u_u
Bon et bien on y arrive.. Tu peux développer / simplifier d'ailleurs.
Fais de même avec l'autre courbe, et puis.. Ben continue ton DM !
J'ai trouvé pour T1 x=-2,5 et pour T2 x=-1
C'est quoi ces "x" ?
