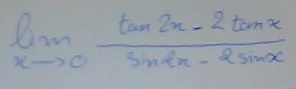Bonsoir,
Je galère à résoudre quelques limites, votre aide est donc le bienvenu !
1) Lim ( 2 - √(3x-2) ) / ( √(2x+5) - 3 ) ( quand x tend vers 2 )
( je suis désolé j'ai vu qu'il y'a des gens qui utilisent des vrais racine carrés et des signes mathématiques mais j'ai pas trouvé)
2) Lim ( √(-3x-2) +x ) / ( x^2 - 1 ) quand x tend vers - l'infini
3) Lim -x + √x / x - 1 ( quand x tend vers + l'infini )
Merci par avance
-----





 et
et 
 Aucune idée, donc partons sur les quantités conjuguées
Aucune idée, donc partons sur les quantités conjuguées