Dérivée - Problème concret

[The_Anonymous]

Bonjour tout le monde!

J'ai un petit souci de compréhension avec un problème, voici l'énoncé :

"On fabrique une boîte sans couvercle avec une plaque de carton carrée de côté en découpant dans chaque coin un carré de côté , la hauteur de la boîte, puis en repliant les côtés. Comment obtenir une boîte de volume maximale?

Indication : Écrire une fonction qui donne le volume de la boîte en fonction de . Déterminer son domaine de définition et trouver son maximum."

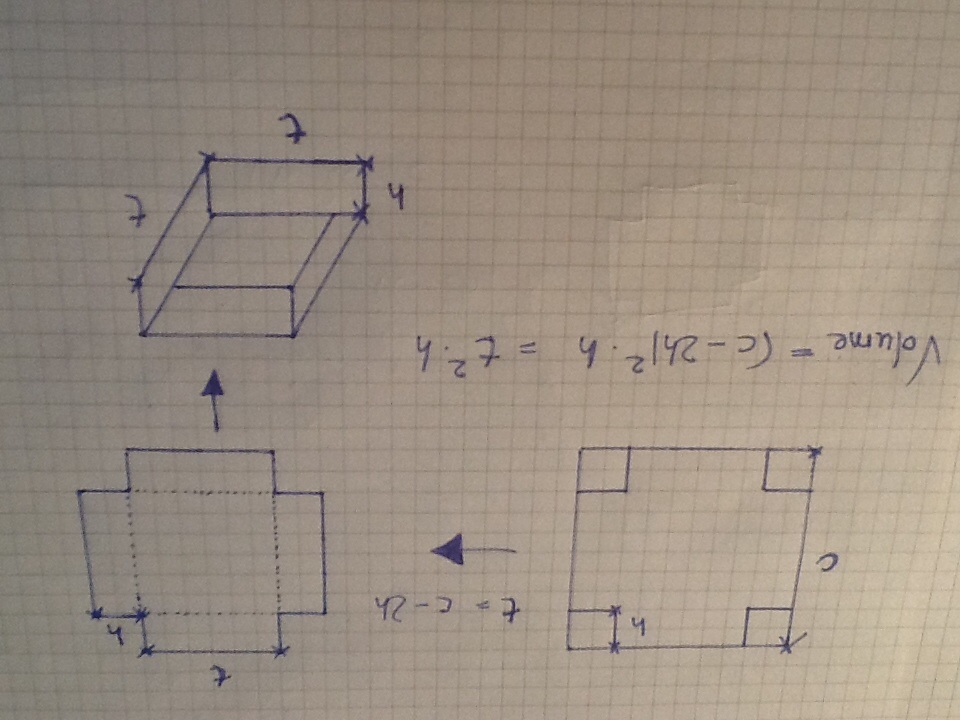
J'ai fait un schéma, le voilà (j'espère avoir compris la fabrication de la boîte) :



Je trouve donc que le volume vaut la hauteur de la boîte, soit multipliée par l'aire du fond de la boîte, qui est carré de côté , donc .

Mais il faut trouver une fonction qui donne le volume en fontion de uniquement. Donc, il faudrait arriver à éliminer ce pour pouvoir ensuite calculer et les racines de la dérivée (déduire le maximum), ce qui ne devrait pas trop me poser de problème.

Mais je n'arrive pas à trouver une fonction qui ne tiendrait compte que de .

Pourriez-vous m'éclairer s'il vous plaît?

Merci d'avance

Cordialement
-----

[Duke Alchemist]

Bonjour.

J'avoue que je ne comprends pas ton problème...

Je trouve donc que le volume vaut la hauteur de la boîte, soit multipliée par l'aire du fond de la boîte, qui est carré de côté , donc .

En reprenant ce que tu as écrit ci-dessus, qu'obtiendrais-tu si tu remplaçait le t² par (c-2h)² dans l'expression de V ?

Duke.

[Gabriel]

V=4h^3 -2ch^2 c^2h

[The_Anonymous]

Bonjour.

J'avoue que je ne comprends pas ton problème...
En reprenant ce que tu as écrit ci-dessus, qu'obtiendrais-tu si tu remplaçait le t² par (c-2h)² dans l'expression de V ?

Duke.

Bonjour,

Je calcule... (Cf ci-dessous)

V=4h^3 -2ch^2 c^2h

xD C'est quoi cette tentative de spoil fail?


Bref, .

Donc, bien que que je n'ai pas trouvé la fonction f(h), le domaine de définition est simplement , donc les solutions trouvés sont correctes.

Est-ce le bon raisonnement?

Merci d'avance !

Édit : ma fonction f(h) n'est-elle pas tout simplement , avec c une constante (le côté du carré initial) ?

Re-Édit : Donc on peut choisir h tel qu'on prend la moitié du côté de c, ou bien alors h tel qu'on prend le sixième du côté c, c'est ça? Mais comme pour c/2, t=0, alors la seule solution est c/6.

[A voir en vidéo sur Futura]

[Gabriel]

Rectif erreur : V=h(c-2h)^2
V=4(h^3) -4c(h^2) +(c^2)h

domaine de définition 0<h<c/2

V'=12(h^2) -8ch +c^2

Pour h=0 => V=0
Pour h=c/2 => V=(c^3)/2

[The_Anonymous]

Désolé pour le double-post, j'ai répondu trop vite.

En fait, la racine c/2 est le minimum, donc cette solution ne nous intéresse pas, mais c/6 est le maximum, donc la réponse est h=c/6, et on obtient le volume .

Cordialement

Édit :

Rectif erreur : V=h(c-2h)^2
V=4(h^3) -4c(h^2) +(c^2)h

domaine de définition 0<h<c/2

V'=12(h^2) -8ch +c^2

Pour h=0 => V=0
Pour h=c/2 => V=(c^3)/2

C'est vrai que le domaine de définition est correct ainsi, et on voit que la solution c/2 est exclue.

Par contre si h=c/2, V=0

[Duke Alchemist]

Re-

Édit : ma fonction f(h) n'est-elle pas tout simplement , avec c une constante (le côté du carré initial) ?

En effet, c'est bien l'expression du volume V(h) de ta boîte.

Re-Édit : Donc on peut choisir h tel qu'on prend la moitié du côté de c, ou bien alors h tel qu'on prend le sixième du côté c, c'est ça? Mais comme pour c/2, t=0, alors la seule solution est c/6.

Tu te rends compte que si h=c/2 alors la base de ta boîte se trouve avec un côté nul. Par conséquent seul c/6 a une signification ici.

Duke.

EDIT : ta boîte aura une base de 2c/3 de côté et une hauteur de c/6

[The_Anonymous]

Re-
En effet, c'est bien l'expression du volume V(h) de ta boîte.

Tu te rends compte que si h=c/2 alors la base de ta boîte se trouve avec un côté nul. Par conséquent seul c/6 a une signification ici.

Duke.

EDIT : ta boîte aura une base de 2c/3 de côté et une hauteur de c/6

Merci beaucoup pour toutes les indications supplémentaires!

(Désolé je n'avais même pas remarqué que vous aviez répondu :S)

À la prochaine sur un autre topic

Cordialement

[Gabriel]

V=4(h^3) -4c(h^2) +(c^2)h la variable est h , c est une constante

V'=12(h^2) -8ch + (c^2) la dérivée V' s'annule pour h1=c/6 et h2=c/2

Lorsque la dérivée est nulle, celà signifie que la fonction V passe par un extremum (maximum local ou minimum local) ou bien passe par un point de torsion.

V'' = 24h -8c la dérivée seconde est toujours positive dans l'intervalle 0<h<c/2 donc h1 et h2 ne sont pas des points de torsion.