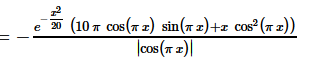Bonjour, tous le monde ! Dans un DM, je dois répondre à la question :
La fonctionest-elle dérivable en 0.5
Premièrement, je me rappelle plus exactement de la méthode ( Regarder le nombre dérivée des deux cotés avec le taux d'accroissement ), et si c'est bien celle dont je me rappelle, elle est juste inapplicable ici.
Je ne cherche pas a avoir directement la réponse, mais plutôt à bien comprendre. Merci d'avance
A mon avis il faut en effet s'intéresser au taux d'accroissement :
tu t'intéresses à la fonction g qui à x associe (f(x)-f(0.5))/(x-0.5). Tu calcules la limite quand x tend vers 0.5, si c'est une limite finie, alors elle est dérivable. Sinon, elle ne l'est pas.
En outre : le produit de deux fonctions dérivables est dérivable.
Pour traiter le cas de la valeur absolue, tu peux distinguer deux cas, en sachant que
si f est "dérivalbe à gauche et à droite de a avec le même nolmbre dérivé, alors elle est dérivable.
Supprimé ...
Dernière modification par PlaneteF ; 04/01/2014 à 15h55.
Ben voilà, c'est ce que j'ai voulu dire mais en beaucoup moins claire ^^
En fait j'ai carrément supprimé le message car je voulais changer plusieurs choses dedans, ... mais pas le temps dans les 5min impartiesEnvoyé par Samuel9-14
, ... donc j'ai préféré le supprimer quitte à le refaire plus tard quand j'aurai plus de temps et en fonction des éventuelles autres réponses !
Cdt
Dernière modification par PlaneteF ; 04/01/2014 à 16h07.
Oui, j'ai déjà fait ça, mais je tombe sur une grosse forme indéterminé, que je n'arrive pas à résoudre !
Tu arrives sur une forme indéterminée ??
Il ne faut t'intéresser qu'au troisième facteur de ta fonction (la valeur absolue).
Tu "traduis" la valeur absolue dans le cas où x>0.5 et dans le cas où x<0.5. Pour la faire "disparaitre". Et après je ne vois pas de forme indéterminée...
Bonsoir.
Une autre façon de faire est de remarquer que la dérivée à gauche est celle de
Il est facile de voir que la dérivée à droite est celle de -g. Donc si g'(0,5) n'est pas nul ...
Cordialement.
Salut gg0, ... tu voulais dire g'(0,5) (juste pour que Sulli96 ne s'embrouille pas)
Cdt
Dernière modification par PlaneteF ; 04/01/2014 à 17h30.
moi je dis que g est paire
Tout à fait.
Merci PlaneteF.
Ce satané ', j'étais persuadé de l'avoir écrit
Salut l'ami ! ... Oui, mais pour la question posée cela ne sert pas.moi je dis que g est paire
Cdt
Dernière modification par PlaneteF ; 04/01/2014 à 17h36.
Donc, si j'ai bien compris, je dois me servir de la dérivé de G, pour trouver le nombre dérivée. En utilisant un logiciel, je trouve ça comme dérivée :
ça me parait bien bien compliqué, donc je me dit que j'ai pris le mauvais chemin.
Pour ta technique Samuel9-14, quand je parle de forme indéterminé je parle de ça :
Si je remplace tous les x par 0.5, je tombe sur un cos ( Pi/2 ) donc cos = 0, et j'ai ma forme indéterminé.
Merci de l'aide que vous m'accordez
Pas besoin d'un quelconque logiciel pour montrer que
Cdt
Dernière modification par PlaneteF ; 04/01/2014 à 18h35.
Certes, mais à quoi ça nous sert de connaître que
Nous ce qu'on veut c'est connaître le nombre dérivé de chaque coté non ?
Oui.
Mais à gauche on a g=k et à droite on a g=-k (d'après ce que disait gg0), donc si k est différent de 0, alors la fonction n'est pas dérivable.
Relis attentivement le message#8 de gg0 (et la petite correction en message#9) : Cela répond totalement à ta question.Certes, mais à quoi ça nous sert de connaître que
Nous ce qu'on veut c'est connaître le nombre dérivé de chaque coté non ?
Edit : Croisement de messages !
Dernière modification par PlaneteF ; 04/01/2014 à 18h42.
C'est bon, je viens de tout comprendre, merci beaucoup. J'avais pas compris l'idée qu'on pouvait sortir la valeur absolue d'un coté vu que le cos > 0
