Statistique : probabilité élémentaire

[Leviss]

Bien le bonjour à tous,

Je ne suis plus étudiant mais je m’intéresse toujours de près, aux mathématiques et la physique.
Aujourd'hui, je tende de comprendre un peu un chapitre particulier, celui des statistiques de probabilité et l'on m'a donné un exercice afin que je puisse voir par moi-même de quoi cela parle.

Voici donc l'exercice :

Une urne contient 2 boules noires et 8 boules blanches.
On prélève une boule au hasard dans l'urne.
Toutes les boules ont la même probabilité d'être prélevées.
On désigne par N l'événement :"la boule prélevée est noire"
On désigne par B l'événement :"la boule prélevée est blanche"

1) construire l'arbre de probabilité correspondant à cette épreuve de Bernoulli
2) trois prélèvements dans l'urne sont successivement réalisés en remettant à chaque fois la boule dans l'urne avant d'effectuer le prélèvement suivant.

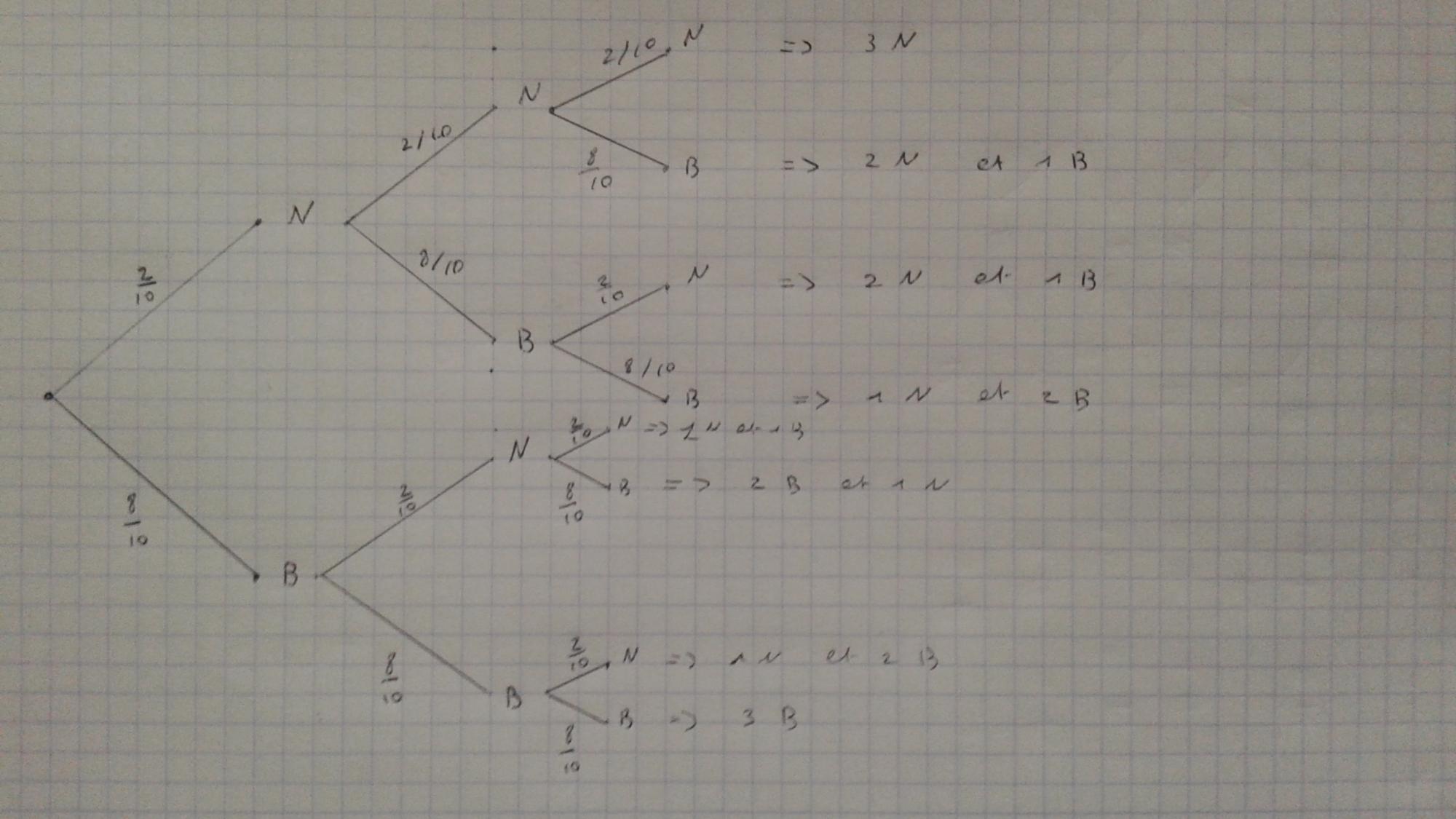
a. Représenter cette épreuve par un arbre pondéré
b. Calculer la probabilité de l'événement E: " obtenir trois boules noires"
C. On désigne par F l’événement : "obtenir exactement 2 boules noirs" Calculer la probabilité de l'événement F

Résolution :

Donc pour la question 1)

-Un arbre de probabilité est donc un schéma représentatif d'une expérience de statistique.
-épreuve de Bernoulli : cela veut donc dire que chaque prélèvement est indépendant des autres (on remet donc les boules avant le prélèvement suivant)



Pour la question 2)

a)
-Un arbre pondéré est donc pour moi l'arbre de probabilité pour 3 prélèvement et pondéré dans le sens où il y a les chiffres de probabilité pour avoir telle ou telle boule

donc nous avons à chaque fois, vu que nous remettons les boules 2 chances sur 10 de tomber sur une boule noir (0,2) et 8 chances sur 10 de tomber sur une boule blanche (0,8)

b) c)

je suis un peu perdu, je sens que l'on doit utiliser calcul de suite mais j'ignore comment.
Pourriez vous m'aider

Merci d'avance,
LEvis
-----

[Leviss]

je pense avoir trouvé les probabilités de tomber sur 3 boules noirs lors de 3 tirages.

Donc pour la question 2)B

Nous avons donc qu'une seul possibilité selon l'arbre de probabilité de tirer lors de 3 tirages, 3 boules noires.
Il faut donc multiplier chacune des probabilité des boules noires entre elles (je pense)

Cela nous donnerai : 2/10 * 2/10 * 2/10 = 1/125 soit 0,008


Est-ce bien juste ?

Pour la question 2)C, je ne la comprend pas

[gg0]

Bonjour.

Ton arbre n'est pas pondéré. Par exemple, pour le premier tirage, il y a en fait 2 branches pour N et 8 pour B. On les représente par une branche marquée 2 pour N et une autre, marquée 8 pour B (arbre des cas); ou bien on note les probabilités sur les branches- ce que tu dis dans le a).

Question 2 a) : " multiplier chacune des probabilité des boules noires entre elles (je pense) ". Oui, mais pourquoi ? Il y a dans les cours de probas élémentaires, les explications des cas où on ajoute les probabilités et où on multiplie des probabilités. Tu dois les connaître pour calculer avec certitude.
Question 2 c) : on veut obtenir 2 boules noires, mais pas 3. Avec un arbre vraiment pondéré avec les probabilités qui se multiplient, on obtient en bout de branche une probabilité. Ne reste plus qu'à appliquer les règles de calcul dont je parlais ci-dessus.
Au fait, peux-tu les citer ?

Cordialement.

[Leviss]

Bonjour gg0 et merci de votre réponse.

je m'intéresse aux probabilités du faite que c'est un chapitre assez conséquent qui ne m'a pas été donné de voir du faite qu'il ne faisait pas partie du programme scolaire à l'époque.
Je n'ai donc pas vraiment de support afin de pouvoir trouver un début et une fin dans mon étude.

Je lis quelques notes sur internet, fait des liens et essaie de comprendre les choses donc si vous avez un lien qui peut m’amener à un cours complet, avec les règles, les exceptions et bien sur des exercices, cela me serait bien utiles.

Donc nous sommes dans une épreuve de Bernoulli (expérience où chaque tirage est indépendant).


J'ai vu une vidéo sur les arbres de probabilité ( http://www.methodemaths.fr/video_proba.php )

ainsi j'ai pu comprendre que lorsqu'il n'y a qu'une possibilité, on multiplie les pondérations de la branche
et si il y en a plusieurs, on addition le résultats des multiplications des pondération de chaque branche.

Nous arriverons donc ainsi a déterminer la loi de probabilité X selon Bernoulli


voici donc mon arbre pondéré



cette arbre répond donc à la question 1) 2)a

concernant la question 2)b
Vous me dites donc que cela est bien la méthode pour y arriver mais je n'ai pas trouvé, mise à part la vidéo, qui montre le pourquoi tu comment et en mathématique, il est primordiale de se raccrocher non pas a des vidéos de youtube mais des théorèmes et preuve. donc si vous pouviez me donner un lien que je puisse m'appuyer sur quelque chose de concret.

Concernant la question 2)c

nous avons 3 branches qui nous donne 2N et 1B

donc d'après mon arbre :

(2/10 * 2/10 *8/10 )+ (2/10 * 8/10 * 2/10) + (8/10 * 2/10 * 2/10) = 12/125


Est ce bien juste d'un point de vue pratique ?

[A voir en vidéo sur Futura]

[gg0]

Ok.

Je vais alors te guider, pour t'éviter un apprentissage flou comme fut le mien (je n'ai jamais eu de cours de probas, je les ai apprises dans le bouquin de ma sœur pour l'aider à faire ses exercices, puis plus tard, pour les enseigner).
On additionne des probas d'événements incompatibles afin d'avoir la proba de leur réunion :

C'est le cas des événements qu'on a aux feuilles des arbres.
On multiplie les probas grâce à la règle des probabilités composées :

qui se généralise bien. C'est ce qu'on utilise quand on parcourt un arbre bien fait (ce sont bien des probas "sachant que" qu'il y a dès le deuxième niveau). Ça se simplifie si les événements sont indépendants, comme dans le cas de ton exercice (le résultat du deuxième tirage ne dépend pas de ce qu'on a eu au premier- ce serait différent avec un tirage sans remise) :
Si A et B sont indépendants,

En tout cas, il serait préférable de prendre un vrai cours de probabilités, plutôt que de piocher des vidéos (j'en connais des totalement fantaisistes !!), sur papier, qui te permettrait d'y revenir souvent. Je t'envoie par MP un cours que je faisais en IUt.

Cordialement.

[Leviss]

Merci à vous gg0,

Je vois que malgré tout, vous vous en êtes sorti vu que vous l'enseigné
je commence doucement a comprendre le tout.

Sinon, mes résultats sont juste pour cette exercice ?

[gg0]

Je trouve comme toi

(en général, on se tutoie sur les forum, ne me renvoies pas mon âge )

[Leviss]

un tout grand merci pour les fichiers, je les ai bien reçu.
Je vais essayer de tutoyer mais bon, ce n'est pas évident