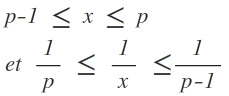Inégalité logarithme népérien et nombres premiers

[KINDERMAXI]

Bonjour,

Je me permet de poster pour avoir un peu d'aide sur une inégalité sur laquelle je bloque. On a p un nombre premier quelconque, et il faut démontrer que :



Au départ, je suis partie de la propriété qui énonce que est égal à . De là, j'ai trouvé que est égal à . Ainsi, comme au départ de l'exercice on a montré que ln(1+x) ≤ x, la première partie de l'inégalité est immédiate. A moins que je me serais trompée à un endroit ?

Cependant, c'est l'autre membre de l'inégalité qui me pose plus de problème, soit :



J'ai notamment essayé de montrer que , sauf qu'ensuite on arrive à , et donc ça donne pas grand chose. Et je vois pas trop comment faire sinon.

Quelqu'un pourrait-il m'aider un peu ?

Merci d'avance !
-----

[Médiat]

Bonjour,

est égal à

Ceci est faux, la bonne relation est :

[KINDERMAXI]

La puissance -1 porte bien sur la parenthèse dans -ln(1-1/p)^-1, non ? Si c'était le ln qui portait la puissance -1, n'aurait-on pas ?

[gg0]

La notation est piègeuse, mais le calcul est automatique : On calcule l'argument du ln, qui est dans la parenthèse, c'est x, puis on lui applique le ln, ça donne ln(x), puis (ordre de l'écriture, qui est celui à suivre s'il n'y a pas d'indication contraire) on applique l'exposant.

N'importe comment, ce serait faux si c'était -ln(x).

Cordialement.

[A voir en vidéo sur Futura]

[gg0]

A noter : Ce n'est pas le ln qui porte l'exposant -1. D'ailleurs la notation est à éviter, car elle peut désigner soit la fonction réciproque de ln, l'exponentielle, soit la fonction "inverse", donnant qui n'a rien à voir avec l'exponentielle.
Autre chose : les parenthèses de fonction font partie de l'écriture de la fonction : Dans f(x+1) la fonction est notée f( ) et son argument est x+1.

Cordialement.

[KINDERMAXI]

D'accord, merci des explications. J'ai testé pour différentes valeurs de p, notamment avec l'inégalité, et ça marche bien quand on fait le log de l'inverse de 1-1/p. Donc ce serait, dans la notation de cet exercice, le paramètre qui serait à la puissance -1 (ce qui est d'ailleurs logique vu la suite de l'exercice...). Mais la notation est, en tout cas, ambiguë.

Merci des explications en tout cas. Après, je bloque toujours sur la deuxième partie de l'inégalité. :/

[gg0]

Il y a effectivement un problème de notation dans ton énoncé, et la bonne formule est bien

qu'on peut compliquer en

si on veut ! Ou simplifier en

Comme on ne sait rien de ton exercice, difficile de t'aider à utiliser d'éventuelles questions précédentes pour prouver ça. Mais je prouve directement la dernière forme que j'ai proposée en remarquant que si x est entre p-1 et p :

puis en intégrant les trois termes (positifs) de cette inégalité de p-1 à p.

A noter : Le fait que p soit premier, ou même qu'il soit entier ne sert à rien ici. Il faut juste qu'il soit strictement supérieur à 1.

Cordialement.

[Tala97]

Comme on ne sait rien de ton exercice, difficile de t'aider à utiliser d'éventuelles questions précédentes pour prouver ça. Mais je prouve directement la dernière forme que j'ai proposée en remarquant que si x est entre p-1 et p :

C'est plutot,

Et apres integration, on devrait trouver le resultat attendu.

[gg0]

Effectivement, c'est bien 1/x et pas x.

[KINDERMAXI]

Je vous remercie beaucoup de l'aide. J'ai terminé le dm en question et pour le coup, j'ai décidé finalement de montrer que ln(x) >= 1-1/x, pour tout x > 0. Après, ça allait tout seul. En tout cas merci encore de l'aide.

[KINDERMAXI]

J'ai refais l'intégration après coup, et c'est vrai que ça aurait été un peu plus "naturel" dans un sens (c'est probablement ce qui était attendu). Merci beaucoup.

(désolé du double post, il ne me semble pas avoir vu de fonction "edit")

[Tala97]

j'ai décidé finalement de montrer que ln(x) >= 1-1/x, pour tout x > 0.

C'est une propriete tres interressante