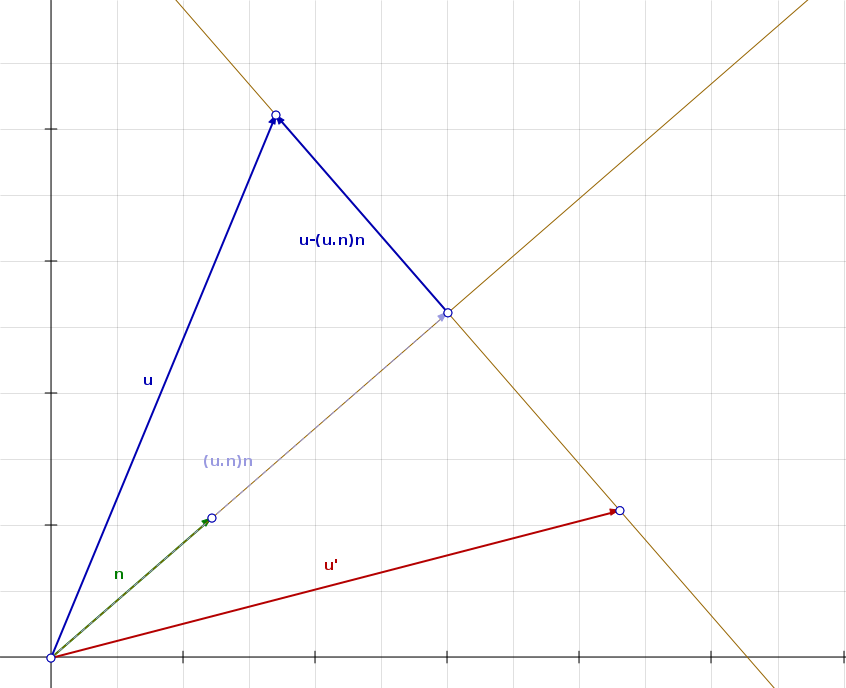
J'ai honte de dire que je trouve des difficultes a resoudre ce systeme, ou les inconnues sont v1' et v2'.
572468fe2efc1bf2f68eb2c712c360fb.png572468fe2efc1bf2f68eb2c712c360fb.png
Voici la solution mais je ne comprends pas comment ils ont pu y arriver
446080a4fe641bb9dca552a69ad2d364.png
Merci pour votre aide.
Bonjour:
Soi le système suivant :
Calculeren fonction de
Cordialement
donc la méthode bourinne est claire. Mais bon, pour un truc plus fin:
tu peux noter que la première equation signifie que la droite passant par (v1, v2) et (v1', v2') est orthogonale à (m1, m2)
La seconde equation que (v1', v2') appartien à une ellipse qui passe aussi par (v1, v2). Peut etre si on connait les propriétés d'une ellipse, on peut s'en sortir.
Sinon, on modifie le problème, on pose u1=sqrt(m1)v1, et u2=sqrt(m2)v2. idem pour les '. Ensuite on réecrit le systeme. L'equation 1 devient la droite passant par (u1, u2) et (u1', u2') est orthogonale à un vecteur [sqrt(m1), sqrt(m2)]. Et les 2 appartiennent à un cercle centré à l'origine.
En clair (u1', u2') est l'image de (u1, u2) par symétrie orthogonale par rapport à la droite passant par l'origine et selon le vecteur [sqrt(m1), sqrt(m2)], ou encore le vecteur unité [sqrt(m1)/[m1+m2], sqrt(m2)/[m1+m2]].
La il faut appliquer une résultat qui dit que la matrice
[n1^2-n2^2 ; 2n1 n2 \\ 2n1 n2 ; n2^2-n1^2] représente la symétrie orthogonale par rapport à la droite passant par 0, et de vecteur directeur [n1, n2] unitaire.
Ca a l'avantage de donner le résultat directement sous la forme voulue.
Il me semblerait que le vecteurEnvoyé par untruc
daum_equation_1433663439130.png
ne soit pas unitaire.
En effet,
daum_equation_1433663655730.png
Le vecteur unitaire ne serait-il pas
daum_equation_1433663803108.png
Et par rapport a la matrice, est-ce que celle-ci donne les nombres u1, u2, u'1 et u'2?
Merci beaucoup pour votre aide, c'est tres interressant de resoudre un systeme geometriquement. Merci egalement pur topmaths!!!
oui, dans le dénominateur c'est plutot sqrt(m1+m2)
La matrice de la symétrie relie (u_1', u_2') à (u_1, u_2)
si le vecteur n est écrit sous la forme
prenons des exemples simples:
donc les points u et u' sont liés par
ou encore
u_1'=-u_1
u_2'=u_2
bien sur ca parrait évident en regardant un dessin.
Un autre exemple, \theta=\pi/4. La matrice devient:
et l'equation
se réduit à
u_1'=u_2
u_2'=u_1
ce qui est correct pour une symétrie par rapport à la première bissectrice.
Reste juste à comprendre d'ou sort cette matrice
Si u est un point, sa projection sur la droite // n, passant par l'orginne est
Le symetrique u' par rapport à la droite //n (cf le dessin pour comprendre):
Et l'ecriture sous forme matricielle de ca donne:
Maintenant, je ne sais pas ce qui est dans ton programme. Mais le calcul de produit de matrices 2x2 doit etre ok. à verifier.
aussi fait attention, cette représentation matricielle simple de la symétrie orthogonale, marche car l'axe de symétrie passe par 0. En effet l'origine a pour image elle meme. Ne t'amuses pas à l'utiliser n'importe comment.
C'est extraordinaire! Merci beaucoup pour cette explication tres exhaustive.
J'attends pour que la piece jointe soit validee pour y jeter un coup d'oeil, merci infiniment.
Le dessin est tres clair encore merci!!!
Le dessin est tres clair, merci encore!!!
