fonction exponentielle

[TOUCALY]

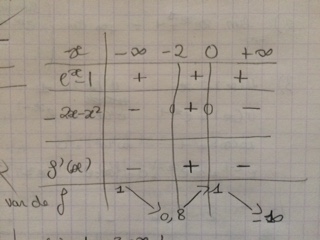
Bonjour, on me donne une fonction définie sur R : f(x) = xexp(x-1) +1
Dans une première partie cette fonction a été étuidée (limites, variations)

Dans la partie B : Recherche d'une tangente particulière :
1) équation de Ta au point d'abscisse a (strictement positif) : y = (a+1)e^a-1x+1-a²e^a-1
2) quand Ta passe par l'origine du repère on a l'égalité suivante 1-a²e^a-1=0 que j'ai démontré sans soucis.
3) le problème se pose la :
Dans cette question toute trace de recherche, même incomplète, sera prise en compte dans l'évaluation. Démontrer que 1 est l'unique solution sur l'intervalle ]0;+infini[ del'équation : 1-x²e^x-1=0
J'ai utilisier la localisation d'une solution d'équation a l'aide d'un tableau de variation mais je ne sais pas si cette méthode est vraiment pertinente:
On prend f(x) = 1-x²e^x-1
f'(x) = e^x-1(-2x-x²)
On étduie les variations de f (voir tableau ci dessus)
lim x->+infini f(x) = - infini et limx->-infini f(x) = 1

Ainsi D'après le tableau de variation :
0 appartient à ]1;-inf[ donc l'équation f(x)= 0 admet une unique solution alpha dans ]0;+inf[. Al'aide de la calculatrice on trouve la valeur de alpha qui est 1.
-----

[PlaneteF]

Bonjour,

]1;-inf[

C'est quoi cet intervalle ?!! ... Il faut écrire :

Sinon connais-tu le théorème des valeurs intermédiaires ?

Cordialement

[TOUCALY]

et ben c'est pas ce que je viens d'appliquer ?

[gg0]

Bonjour Toucaly.

Si tu viens d'appliquer un théorème, où est le problème ? Car tu disais "je ne sais pas si cette méthode est vraiment pertinente".

Cordialement.

[A voir en vidéo sur Futura]

[PlaneteF]

et ben c'est pas ce que je viens d'appliquer ?

Déjà lorsque l'on applique un théorème, on le cite. Ensuite un point essentiel dans le théorème des valeurs intermédiaires est la continuité de la fonction, chose que tu n'évoques pas du tout ! ... Par ailleurs où montres-tu l'unicité de la solution ?

Cdt

[TOUCALY]

Je me posais juste la question de savoir si la méthode que j'ai utiliser pour démontrer ce qu'on m'a demandé était assez pertinente ou si il fallait démontrer plus par calcul ?

[PlaneteF]

Je me posais juste la question de savoir si la méthode que j'ai utiliser pour démontrer ce qu'on m'a demandé était assez pertinente ou si il fallait démontrer plus par calcul ?

Non elle n'est pas suffisamment pertinente. Cf. message#5

Cdt

[PlaneteF]

... Et je précise un peu plus :

1) L'existence de la solution est donnée par la continuité de la fonction sur l'intervalle en question et par l'application du T.V.I. ;

2) L'unicité de la solution est donnée par la stricte monotonie de la fonction sur l'intervalle en question.

A toi de faire une rédaction de la démonstration à partir de ces 2 éléments.

Cdt