- Soient
f(x) = cos x
g(x) = √(2x+π²)
Déterminer f ◦ g et g ◦ f et indiquer leur domaine de dé finition.
Alors pour f ◦ g, j'ai trouvé le domaine de définition, en ayant passé les membres à gauche pour donner 2x>ou=-π² et donc x>ou=-π²/2
Mais comment on s'y prend pour g ◦ f? J'ai essayé de faire arcsin sur la calculette pour trouver x mais j'ai une erreur
Merci d'avance
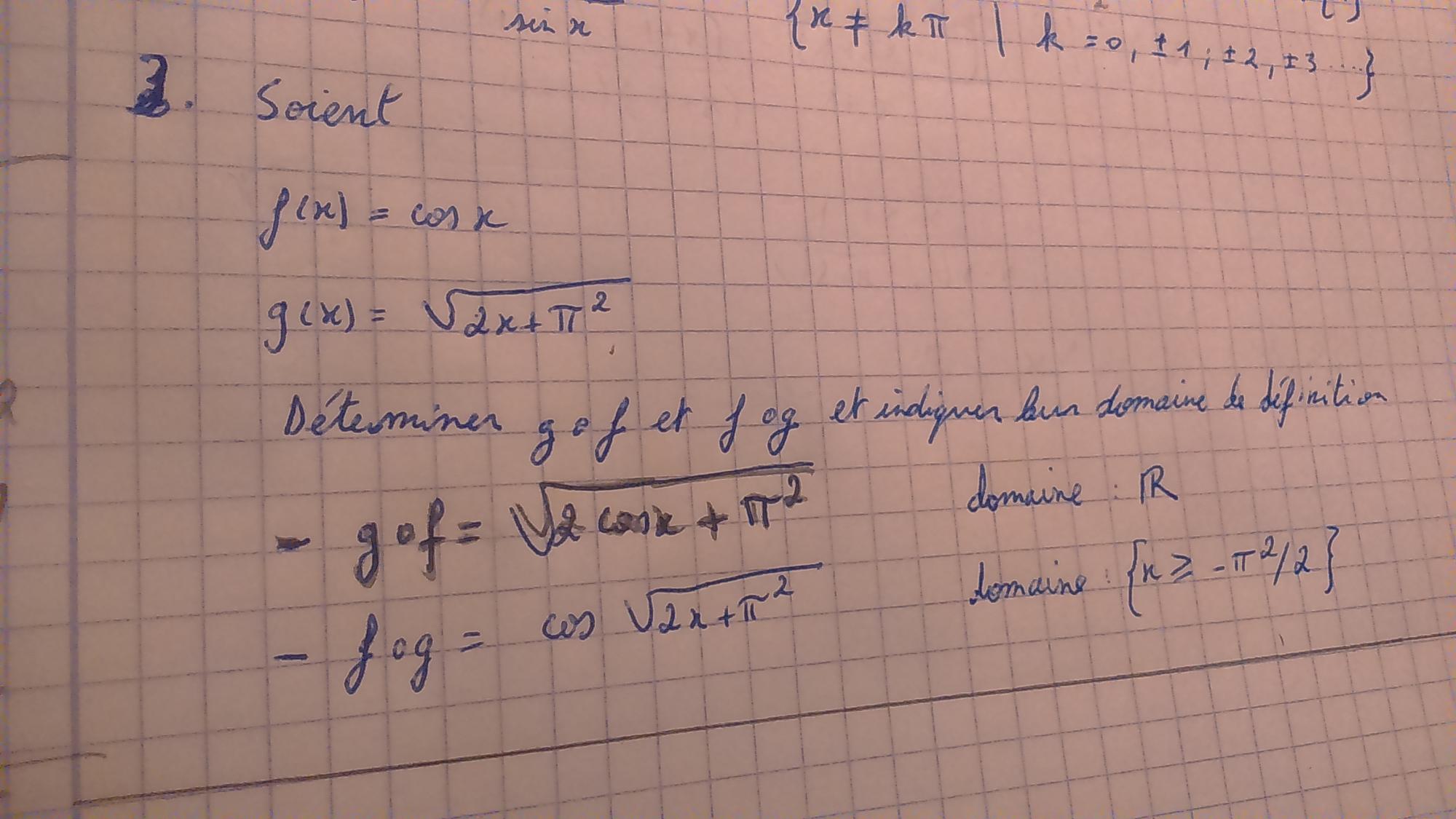
"J'ai essayé de faire arcsin..."
Je voulais dire arccos.
Il suffit de résoudre l'inéquation 2cos x +π²>0 ce qui donne cos x>-π²/2 or on a -1≤cos≤1 donc ta fonction est défini sur R puisque cos x est toujours supérieur à -π²/2.
PS: Comme cos x ne peut pas être egal à -π²/2 pas étonnant que tu as une erreur lorsque tu fais arccos (-π²/2).
Bonne soirée.
Pour g ◦ f, j'ai:
g ◦ f=
Donc pour trouver le domaine de définition on aura:
si on transforme en degrés:
16200° et cela équivaut à 16200/360=45 tours de 360°
Ensuite je suis perdu, je ne sais, même pas si j'ai résonné de la bonne façon pour chercher le domaine de g ◦ f.
La réponse de l'énonce c'est R (domaine). Mais pourquoi et comment?
Merci d'avance
Attention,
il n'y a pas de degrés ici. -π²/2 vaut environ -5. pas -5 degrés ou -5 radians, -5 tout court. C'est la mesure des angles qui donne des degrés ou des radians. Mais la fonction cosinus des maths est simplement appliquée à un nombre pur. Cependant, les cosinus des angles ont un lien et le cosinus d'un angle de mesure x radians est cos(x).
Relis le message de Worgui.
Bonsoir Worgui, merci beaucoup d'avoir répondu.Envoyé par worgui
Il suffit de résoudre l'inéquation 2cos x +π²>0 ce qui donne cos x>-π²/2 or on a -1≤cos≤1 donc ta fonction est défini sur R puisque cos x est toujours supérieur à -π²/2.
PS: Comme cos x ne peut pas être egal à -π²/2 pas étonnant que tu as une erreur lorsque tu fais arccos (-π²/2)
Bonne soirée.
Donc -π²/2 donne bien 1 sur l'axe de cosinus vu qu'on fait 45 tours de -360°?
Mais alors je ne comprends pas pourquoi tu as dit "cos x est toujours supérieur à -π²/2", il ne peut pas être égal à -π²/2 si cela donne 1 sur l'axe de cosinus?
Merci d'avance
Bonsoir,
UN GRAND MERCI A VOUS DEUX!
Je viens de comprendre mon erreur, j'ai eu beaucoup de mal à me représenter ce problème en tête, mais je vois un peu plus clair maintenant.
C'est donc effectivement le domaine R la solution.
Encore merci
Le cercle trigo est un cercle de rayon 1 c est pourquoi sin x et cos x sont compris en -1et1 or -π²/2 est inférieur à -1 donc -π²/2 sera à l'extérieur du cercle trigo (on se place évidemment dans un repère orthonormé dont l'origine est le centre du cercle trigo ) et donc comme -π²/2 est à l'extérieur du cercle il n'existe pas de cos qui soit égale à cette valeur. Aussi le x dans cos x représente un angle en degré ou en radian alors que cos x représente une longueur c 'est à mon avis cela que tu as mal compris cependant cos(-π²/2) existe (même si je ne sais pas placé cette valeur sur le cercle trigo).
C'est exactement cette erreur de compréhension qui m'a un peu perturbé et j'ai effectivement pensé que le cosinus d'un angle était égal à un angle en degré ou radians, pire encore, je pensais que les valeurs en
